Je suis nettement plus enthousiaste déjà ! Pour 3 joueurs, on trouve donc
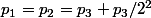
et vous avez réussi à m’inspirer (enfin je crois même si cela gagnerait surement à être mieux rédigé)
Redémontrons le résultat de GaBuZoMeu :
Si 1 laisse sa place dans le 1er match pour jouer en dernier
- Il perd son avantage de jouer en premier
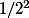
qui va être donné au joueur 3 c'est à dire
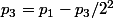
- Lorsque 2 prend la place de 1 alors rien ne change pour lui donc
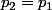
- Lorsque 3 prend la place de 2 alors il gagne
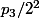
donc
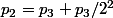
Mais alors pour

individus, qu'est-ce qui se passe ?
Si 1 laisse sa place dans le 1er match pour jouer en dernier
- Il perd son avantage de jouer en premier
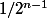
qui va être réparti entre les joueurs 3,4 ... n c'est à dire
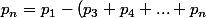/2^{n-1})
- Lorsque 2 prend la place de 1 alors rien ne change pour lui donc
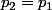
- Lorsque 3 prend la place de 2 alors il gagne
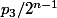
donc
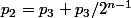
- Lorsque 4 prend la place de 3 alors il gagne
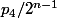
donc
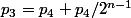
...
- Lorsque n prend la place de n-1 alors il gagne
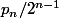
donc
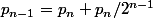
Si je ne me suis pas loupée, en tout cas c'est correct pour n=3, n=4 et n=5, on démontre donc que
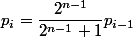
pour
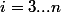
avec
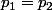
et
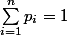
PS : Si vous êtes intéressés, je peux vous retranscrire la démonstration de Bernoulli pour n=5, elle vaut quand même le détour si vous n'êtes pas fâchés avec les systèmes d'équations ayant pas mal d'inconnues. En plus, elle a l'avantage d'être transposable assez facilement pour les espérances. C'est l'objectif suivant, on ne se décourage pas



