Bonjour j'ai besoin d'aide pour implémenter un algorithme pour pouvoir approximer la solution quelque soit les paramètres.En effet on parle d'un algorithme pour Matlab sur les méthodes des différences finies.Pouviez vous m'aider ? :
-u''(x) + c(x) u(x) = f(x) ; 0 < x < L ; (1)
u(0) = alpha ; (2)
u(L) = beta : (3)
Probleme aux limites sur les methodes des differences finies
5 messages
- Page 1 sur 1
Re: Probleme aux limites sur les methodes des differences fi
Bonjour
Si tu as vu le cours la résolution du problème se résume à la solution d'un système linéaire (de taille assez grande).
Si algorithme il y a, je n'en vois pas, sauf celui de la résolution du système linéaire . Le tout est de savoir écrire l'équation .
Sur le lien suivant tu peux voir le système (cf 3.3) qui correspond à peu de chose près à ton problème.
https://moodle.insa-toulouse.fr/pluginfile.php/68295/mod_resource/content/5/S3-Laplacien-DF.pdf
Il faudra ajouter les termes diagonaux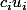 qui correspondent au terme c(x) u(x).
qui correspondent au terme c(x) u(x).
Ensuite du point de vue la résolution numérique du système discrétisé, il faut utiliser le fait que la matrice est creuse (voir la fonction avec matlab qui doit exister en anglais sparse matrix), puis concernant la méthode résolution
tu laisses faire matlab, sinon tu programmes toi même la résolution via une factorisaton LU (ou de Choleski si possible) de ta matrice.
Maintenant il faut voir si la matrice est bien conditionnée. En effet sans le terme c(x) u(x)
la matrice A du système est tridiag_n(-1,2,-1) dont on sait calculer les valeurs propres. En particulier
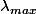 tend vers 4 mais
tend vers 4 mais 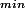 tend vers 0 (quand n tend vers l'infini). Ceci on pouvait si attendre en vertu du th de Gershgorin.
tend vers 0 (quand n tend vers l'infini). Ceci on pouvait si attendre en vertu du th de Gershgorin.
La matrice est donc mal conditionnée. Par contre je ne sais pas si le terme c(x)u(x) arrange les choses. A ce propos je pense que c(x)>0 (n-est ce pas?)
Si tu as vu le cours la résolution du problème se résume à la solution d'un système linéaire (de taille assez grande).
Si algorithme il y a, je n'en vois pas, sauf celui de la résolution du système linéaire . Le tout est de savoir écrire l'équation .
Sur le lien suivant tu peux voir le système (cf 3.3) qui correspond à peu de chose près à ton problème.
https://moodle.insa-toulouse.fr/pluginfile.php/68295/mod_resource/content/5/S3-Laplacien-DF.pdf
Il faudra ajouter les termes diagonaux
Ensuite du point de vue la résolution numérique du système discrétisé, il faut utiliser le fait que la matrice est creuse (voir la fonction avec matlab qui doit exister en anglais sparse matrix), puis concernant la méthode résolution
tu laisses faire matlab, sinon tu programmes toi même la résolution via une factorisaton LU (ou de Choleski si possible) de ta matrice.
Maintenant il faut voir si la matrice est bien conditionnée. En effet sans le terme c(x) u(x)
la matrice A du système est tridiag_n(-1,2,-1) dont on sait calculer les valeurs propres. En particulier
La matrice est donc mal conditionnée. Par contre je ne sais pas si le terme c(x)u(x) arrange les choses. A ce propos je pense que c(x)>0 (n-est ce pas?)
Modifié en dernier par aviateur le 19 Oct 2017, 21:02, modifié 2 fois.
Re: Probleme aux limites sur les methodes des differences fi
Bonjour,je vais travailler pour comprendre la décomposition,je crois que c'est cela mon problème.Merci encore
Re: Probleme aux limites sur les methodes des differences fi
Dans ce cas tu cherches factorisation LU ou bien factorisation de Choleski d'une matrice tridiagonale .
En effet la matrice étant particulière la factorisation se simplifie et de même la résolution des 2 systèmes triangulaires. Il y l'économie en taille et en temps qui est impérative à mettre ne oeuvre dans ce genre de résolution
En effet la matrice étant particulière la factorisation se simplifie et de même la résolution des 2 systèmes triangulaires. Il y l'économie en taille et en temps qui est impérative à mettre ne oeuvre dans ce genre de résolution
Re: Probleme aux limites sur les methodes des differences fi
Donc en gros je me débrouille pour décomposer l’équation a la main pour avoir une matrice tridiagonale et ensuite j'utilise la décomposition LU pour la résolution.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
