Hola :we:
je suis entrain d'attaquer les nombres complexes , mais j'arrive pas à imaginer ce i , dans l'expression i² = -1 ,franchement il me parait un peu mystérieux :hein: , je voudrais savoir quel est l'origine de ce i et pourquoi la lettre i spécialement et quelle est l'utilité de ses nombres complexes en général .
PS: j'ai consulté quelques liens mais je préfère vos suggestions peut etre ça sera plus convaiquant :++:
amicalement
Le i mystérieux
64 messages
- Page 1 sur 4 - 1, 2, 3, 4
par mathador » 08 Aoû 2006, 15:08
Salut
le nombre i n'est pas facile à concevoir, parce qu'un carré négatif ne correspond à rien dans la nature. C'est pour ça qu'on le qualifie d'imaginaire, avec un i ... comme i !
L'origine des complexes est la résolution des équations du 3ème degré (Bombelli, je crois : au lieu de s'arrêter quand il tombait sur "racine de -1", il a poursuivi les calculs, et constaté que les résultats fonctionnaient), mais l'intérêt apparaît dès le second degré :
Si on considère ax²+bx+c=0, avec a,b,c dans R, tu sais qu'on doit calculer le discriminant : D = b²-4ac ; si D>0, on a une formule qu'on connait, avec une racine de D. Mais si D<0 ? Pour prendre sa racine, problème.
L'intéret de i, c'est qu'on peut écrire, pour a réel : (ai)² = a²i² = -a² < 0 ; et ainsi prendre a*i comme "racine carrée" de -a².
A quoi correspond C, ensemble des complexes ? A un plan. Les réels correspondent à une droite (de dimension 1 : pour repérer un réel sur la droite réelle, il suffit de donner sa valeur). Pour les complexes, il faut la partie réelle et la partie imaginaire, donc 2 dimensions : un plan, par exemple. Ainsi, si tu prends un repère orthonormal, tu peux considérer l'abscisse comme la partie réelle, et l'ordonnée comme partie imaginaire.
S'ensuivent quelques définitions : la distance du point (a,b) à l'origine est appelée module, et vaut (thm de Pyhtagore) racine de (a²+b²). L'angle par rapport à l'axe des réels (y = 0) est l'argument. On peut trouver d'innombrables propriétés sur les complexes !
La plus remarquable est sans doute la suivante : C est algébriquement clos (théorème de d'Alembert), ça veut dire que tout polynôme à coefficients dans C peut s'écrire (X-a)(X-b)(X-c)(C-d)...
Dans R, c'est pas le cas : X²+1, par exemple, ça marche pas (alors que dans C, c'est (X-i)(X+i), tu peux vérifier en développant)
Avoir une forme tout factorisée (on dit que le polynôme est scindé), ça a aussi plein d'avantage !
En gros, les complexes, on peut tout faire avec :id: et ce que j'ai dit à propos du plan complexe, notamment, ça apporte beaucoup pour la géométrie.
Je pense avoir déjà beaucoup parlé ... Je passe le relai ! :zen:
Amicalement
le nombre i n'est pas facile à concevoir, parce qu'un carré négatif ne correspond à rien dans la nature. C'est pour ça qu'on le qualifie d'imaginaire, avec un i ... comme i !
L'origine des complexes est la résolution des équations du 3ème degré (Bombelli, je crois : au lieu de s'arrêter quand il tombait sur "racine de -1", il a poursuivi les calculs, et constaté que les résultats fonctionnaient), mais l'intérêt apparaît dès le second degré :
Si on considère ax²+bx+c=0, avec a,b,c dans R, tu sais qu'on doit calculer le discriminant : D = b²-4ac ; si D>0, on a une formule qu'on connait, avec une racine de D. Mais si D<0 ? Pour prendre sa racine, problème.
L'intéret de i, c'est qu'on peut écrire, pour a réel : (ai)² = a²i² = -a² < 0 ; et ainsi prendre a*i comme "racine carrée" de -a².
A quoi correspond C, ensemble des complexes ? A un plan. Les réels correspondent à une droite (de dimension 1 : pour repérer un réel sur la droite réelle, il suffit de donner sa valeur). Pour les complexes, il faut la partie réelle et la partie imaginaire, donc 2 dimensions : un plan, par exemple. Ainsi, si tu prends un repère orthonormal, tu peux considérer l'abscisse comme la partie réelle, et l'ordonnée comme partie imaginaire.
S'ensuivent quelques définitions : la distance du point (a,b) à l'origine est appelée module, et vaut (thm de Pyhtagore) racine de (a²+b²). L'angle par rapport à l'axe des réels (y = 0) est l'argument. On peut trouver d'innombrables propriétés sur les complexes !
La plus remarquable est sans doute la suivante : C est algébriquement clos (théorème de d'Alembert), ça veut dire que tout polynôme à coefficients dans C peut s'écrire (X-a)(X-b)(X-c)(C-d)...
Dans R, c'est pas le cas : X²+1, par exemple, ça marche pas (alors que dans C, c'est (X-i)(X+i), tu peux vérifier en développant)
Avoir une forme tout factorisée (on dit que le polynôme est scindé), ça a aussi plein d'avantage !
En gros, les complexes, on peut tout faire avec :id: et ce que j'ai dit à propos du plan complexe, notamment, ça apporte beaucoup pour la géométrie.
Je pense avoir déjà beaucoup parlé ... Je passe le relai ! :zen:
Amicalement
par nada-top » 08 Aoû 2006, 15:34
salut
merci mathador je vois pas mal de choses maintenant ... si j'ai compris l'origine de i c'est imaginaire puisqu'li n'y a pas de correspondances concrètes dans la nature .
alors d'aprés cela peut-on dire que i et -i sont les solutions de cette équation ? et S s'exprime en fonction de ce i ou quoi??
merci mathador je vois pas mal de choses maintenant ... si j'ai compris l'origine de i c'est imaginaire puisqu'li n'y a pas de correspondances concrètes dans la nature .
Dans R, c'est pas le cas : X²+1, par exemple, ça marche pas (alors que dans C, c'est (X-i)(X+i), tu peux vérifier en développant)
alors d'aprés cela peut-on dire que i et -i sont les solutions de cette équation ? et S s'exprime en fonction de ce i ou quoi??
par Flodelarab » 08 Aoû 2006, 15:43
Moi, ce que je trouve formidable, c l'inventivité de ne plus compter que dans un seul sens (se balladant sur l'axe des réels) mais de compter aussi dans l'autre sens (axe perpendiculaire).
La réalité de ces nombres est si peu évident que personne n'en parle jamais (à part entre scientifiques). Pourtant, c l'ensemble de nombres le plus grand que l'on connaisse, celui qui englobe tous les autres.
Les applications géométriques sont formidables: au lieu de considérer des droites, des points, des formes, on considère le nombre (affixe) qui leur est associé et on peut alors résoudre les problèmes géométriques en faisant, non plus de la géométrie mais de l'arithmétique avec des plus, des multiplés ...
comme ICI par exemple
La réalité de ces nombres est si peu évident que personne n'en parle jamais (à part entre scientifiques). Pourtant, c l'ensemble de nombres le plus grand que l'on connaisse, celui qui englobe tous les autres.
Les applications géométriques sont formidables: au lieu de considérer des droites, des points, des formes, on considère le nombre (affixe) qui leur est associé et on peut alors résoudre les problèmes géométriques en faisant, non plus de la géométrie mais de l'arithmétique avec des plus, des multiplés ...
comme ICI par exemple
par Flodelarab » 08 Aoû 2006, 15:48
un dernier point.
Longtemps les nombres complexes ont été considérés comme un délire de matheux sans réalité physique.
Mais maintenant, personne ne pourrait s'en passer pour exprimer une onde électrique par exemple.
Longtemps les nombres complexes ont été considérés comme un délire de matheux sans réalité physique.
Mais maintenant, personne ne pourrait s'en passer pour exprimer une onde électrique par exemple.
par Mathosi » 08 Aoû 2006, 18:21
mathador a écrit:L'origine des complexes est la résolution des équations du 3ème degré (Bombelli, je crois : au lieu de s'arrêter quand il tombait sur "racine de -1", il a poursuivi les calculs, et constaté que les résultats fonctionnaient
La résolution des équations du troisième degré s'est faite en plusieurs étapes. Del Ferro a trouvé comment en résoudre certaines, d'une forme particulière; Tartaglia a trouvé la méthode générale pendant un concours de mathématiques à Bologne, et a livré sa méthode à Cardan en lui demandant de garder le secret. Mais Cardan trahit Tartaglia et publia la méthode (on raconte que les deux mathématiciens devinrent alors des ennemis irréductibles, à tel point que Tartaglia faillit mourir assassiné...). Bombelli, lui, fut effectivement le premier à exprimer les racines complexes des équations algébriques.
par Mathosi » 08 Aoû 2006, 18:24
nada-top a écrit:j'arrive pas à imaginer ce i , dans l'expression i² = -1 ,franchement il me parait un peu mystérieux
Ne te lance pas dans l'étude des quaternions, alors... :ptdr:
par Chimomo » 09 Aoû 2006, 16:34
Je voudrais approter quelques précisions. la première vraie formalisation (je veux dire construction mathématiques des complexes rigoureuse) fut faites par Hamilton pour la physique, de même que les quaternions.
Il n'ont en fait rien de mystérieux.
Considérons l'ensemble R² muni des deux lois suivantes :
(a,b) + (c,d) = (a+b,c+b)
(a,b).(c,d) = (a.c-b.d, a.d + b.c)
R² est alors muni d'une strcture de corps, le neutre additif est (0,0) et le neutre multiplicatif (1,0). C'est aussi un espace vectoriel. Une base en est ((1,0),(0,1)). Si on note 1=(1,0) et i=(0,1), tout élément de R² s'écrit (a,b) = a +i.b.
On remarque alors que i² = (0,1).(0,1) = (-1,0) = -1.
Voilà donc notre fameux i.
je tiens à ajouter que s'il existe d'autres construciotn des complexes, celle qui sonsiste à dire i² = -1 n'est pas une construction mathématiquement licite de C.
Ce qu'on écrit abusivement
Il n'ont en fait rien de mystérieux.
Considérons l'ensemble R² muni des deux lois suivantes :
(a,b) + (c,d) = (a+b,c+b)
(a,b).(c,d) = (a.c-b.d, a.d + b.c)
R² est alors muni d'une strcture de corps, le neutre additif est (0,0) et le neutre multiplicatif (1,0). C'est aussi un espace vectoriel. Une base en est ((1,0),(0,1)). Si on note 1=(1,0) et i=(0,1), tout élément de R² s'écrit (a,b) = a +i.b.
On remarque alors que i² = (0,1).(0,1) = (-1,0) = -1.
Voilà donc notre fameux i.
je tiens à ajouter que s'il existe d'autres construciotn des complexes, celle qui sonsiste à dire i² = -1 n'est pas une construction mathématiquement licite de C.
Ce qu'on écrit abusivement
par nada-top » 10 Aoû 2006, 00:44
salut à vous tous
désolée de répondre si tard , merci pour vos réponses :happy2:
ça parait convaincant mais pourquoi on note précisemment i = (0,1) :hein:
désolée de répondre si tard , merci pour vos réponses :happy2:
chimomo a écrit:R² est alors muni d'une strcture de corps, le neutre additif est (0,0) et le neutre multiplicatif (1,0). C'est aussi un espace vectoriel. Une base en est ((1,0),(0,1)). Si on note 1=(1,0) et i=(0,1), tout élément de R² s'écrit (a,b) = a +i.b.
On remarque alors que i² = (0,1).(0,1) = (-1,0) = -1.
Voilà donc notre fameux i.
ça parait convaincant mais pourquoi on note précisemment i = (0,1) :hein:
par Sdec25 » 10 Aoû 2006, 00:49
nada-top a écrit:pourquoi on note précisemment i = (0,1) :hein:
Pourquoi pas ?
On a un espace de dimension 2, il faut constituer une base avec 2 éléments : (1,0) et (0,1) (comme la base canonique de R²).
On note ces éléments 1 et i comme on aurait pu les noter a et b.
C'est une manière de construire l'ensemble des complexes, qui permet de dire que tout complexe est combinaison linéaire de 1 et de i et que i²=-1
Et donc on peut écrire un nombre complexe sous la forme a+ib (ce qu'on voit en terminale normalement).
par nada-top » 10 Aoû 2006, 01:09
Sdec a écrit:On note ces éléments 1 et i comme on aurait pu les noter a et b.
mais a et b sont des réels :hein: et i est imaginaire
par Sdec25 » 10 Aoû 2006, 01:16
Qui a dit que a et b sont réels ?
Tu n'as pas dû comprendre ce qu'a dit Chimomo (sur la construction des complexes). On ne parle pas d'imaginaire ni de réels, juste d'un espace vectoriel de dimension 2.
Tu as vu les espaces vectoriels ?
Normalement au lycée quand on voit les complexes on apprend juste que z=a+ib est un nombre complexe, c'est suffisant pour comprendre comment les utiliser.
Mais si je dis 1=(1,0) et i=(0,1) alors 1 et i sont des vecteurs qui forment la base des complexes.
Tu n'as pas dû comprendre ce qu'a dit Chimomo (sur la construction des complexes). On ne parle pas d'imaginaire ni de réels, juste d'un espace vectoriel de dimension 2.
Tu as vu les espaces vectoriels ?
Normalement au lycée quand on voit les complexes on apprend juste que z=a+ib est un nombre complexe, c'est suffisant pour comprendre comment les utiliser.
Mais si je dis 1=(1,0) et i=(0,1) alors 1 et i sont des vecteurs qui forment la base des complexes.
par nada-top » 10 Aoû 2006, 01:33
Tu n'as pas dû comprendre ce qu'a dit Chimomo (sur la construction des complexes
ça c'est sur avec la question que je viens de poser :girl2: ..
pour l'espace vectoriel peut etre on l'a utilisé mais j'ai jamais croisé ces notations
donc j'ai confondu les choses .1=(1,0) et i=(0,1)
je vais chercher ça et je te poserai qq questions si je comprends pas toujours (si tu le permet biensur)....mais la question qui me tente maintenant c'est quoi l'interprétation géométrique de ce i , par exemple si
désolée pour ces questions un peu banales :mur:
par Sdec25 » 10 Aoû 2006, 01:43
Déjà je te rassure en pratique tu n'auras qu'à savoir que i²=1
si tu as des questions pas de problème :happy3:
Pour l'interprétation graphique, dans un repère orthonormé (O, i, j) on a l'axe réel et l'axe imaginaire.
La partie réelle du nombre correspond à sa position sur l'axe réel et la partie imaginaire à sa position sur l'axe imaginaire (l'ordonnée).
Pour le point A correspondant au nombre complexe a+ib, on aura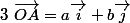
Je ne comprend pas ta question à propos de racine de 2 :hein:
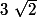est un réel donc sa représentation graphique est un point sur l'axe réel.
je vais chercher ça et je te poserai qq questions si je comprends pas toujours (si tu le permet biensur)....mais la question qui me tente maintenant c'est quoi l'interprétation géométrique de ce i , par exemple si \sqrt{2} : diagonale du carré de coté 1 ; le i représente quoi ???
si tu as des questions pas de problème :happy3:
Pour l'interprétation graphique, dans un repère orthonormé (O, i, j) on a l'axe réel et l'axe imaginaire.
La partie réelle du nombre correspond à sa position sur l'axe réel et la partie imaginaire à sa position sur l'axe imaginaire (l'ordonnée).
Pour le point A correspondant au nombre complexe a+ib, on aura
Je ne comprend pas ta question à propos de racine de 2 :hein:
par nada-top » 10 Aoû 2006, 02:03
sdec25 a écrit: pas de problème si tu as des questions
merci
voilà je viens de trouver ça http://villemin.gerard.free.fr/Wwwgvmm/Type/ImagComp.htm ..voir partie interprétation géometrique.
enfin je vois qq chose de concret ...ouf
pour la racine 2 , c'etait pas une question c'etait juste un ex pour que tu comprenne ce que je veux savoir.
maintenant finissons une fois pour toute avec ce fameux i , je vais l'accepter:briques: ... et ce j ..dans j=-1/2+i\sqrt{3}/{2}
d'ou il vient celui la encore...:hum:
par Sdec25 » 10 Aoû 2006, 02:14
Alors j c'est une racine cubique de 1, tu peux le vérifier en calculant j^3
Un nombre complexe s'écrit sous la forme)
avec comme interprétation graphique pour le point A :
m=OA (module) et)
Soit
, on voit bien que 
Un nombre complexe s'écrit sous la forme
m=OA (module) et
Soit
par nada-top » 10 Aoû 2006, 02:31
Sdec25 a écrit:Alors j c'est une racine cubique de 1, tu peux le vérifier en calculant j^3
Un nombre complexe s'écrit sous la forme
m=OA (module) et
Soit
ah la je vois pas mal de choses qui sont nouvelles pour moi , il faut peut etre se lancer dans la pratique , question de se familiariser d'abord avec cette forme algébrique z=a+ib et aprés je vais voir ces trucs...
merci boucoup Sdec pour toutes ces précisions , c'etait vraiment sympa
mais surement j'aurai d'autres questions demain
n'oublie pas :ptdr:Scdec25 a écrit:si tu as des questions pas de problème :happy3:
merci encore :++:
PS: d'ou il sort ce petit e encore :hum:..non je rigole ne te fatigue pas je vais chercher.
par Sdec25 » 10 Aoû 2006, 02:34
de rien :zen:
Le e c'est simplement exponentielle, tu verras ça l'année prochaine :happy3:
à demain :we:
Le e c'est simplement exponentielle, tu verras ça l'année prochaine :happy3:
à demain :we:
par Chimomo » 10 Aoû 2006, 12:22
Une autre remarque géométrique intéressante, multiplier un complexe par i revient à faire une rotation de 90° dans le plan.
On observe évidemment que multiplier deux fois par i revient à faire une rotation de 180° donc à multiplier par -1.
On retrouve i²=-1
On observe évidemment que multiplier deux fois par i revient à faire une rotation de 180° donc à multiplier par -1.
On retrouve i²=-1
par Flodelarab » 10 Aoû 2006, 12:56
Hum! A ceci près que multiplier par i est une rotation de 90° et multiplié encore par i de 180°.Chimomo a écrit:Une autre remarque géométrique intéressante, multiplier un complexe par i revient à faire une rotation de 45° dans le plan.
On observe évidemment que multiplier deux fois par i revient à faire une rotation de 90° donc à multiplier par -1.
Ben oui, pour retomber sur l'axe des réels purs ....
64 messages
- Page 1 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :