C'est un problème de minimisation : tu recherches la valeur de a telle que E((\Theta-a)^2) soit minimale.
Il se trouve que cette fonction est de degré 2, et admet un minimum, en la valeur E(\Theta).
Est-ce plus clair?
MOOC : Probability from MIT
65 messages
- Page 4 sur 4 - 1, 2, 3, 4
Re: MOOC : Probability from MIT
merci LB2 mais ce n'est pas la recherche du minimum qui me pose probleme.
si je comprends bien, on connait la distribution a priori de notre variable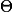 mais on ne connait pas son Esperance. On a choisi un estimateur a priori
mais on ne connait pas son Esperance. On a choisi un estimateur a priori 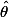 pour la variable
pour la variable 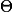 .
.
puis on tente de calculer le minimum de l'erreur. Mais puisque il n'y a pas d'observations qu'est ce que c'est que cette quantité^2 ]) ? . Serait on assez bête pour choisir un
? . Serait on assez bête pour choisir un 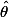
qui ne correspond pas a l'Esperance de notre distribution choisie arbitrairement) a priori ?
a priori ?
si je comprends bien, on connait la distribution a priori de notre variable
puis on tente de calculer le minimum de l'erreur. Mais puisque il n'y a pas d'observations qu'est ce que c'est que cette quantité
qui ne correspond pas a l'Esperance de notre distribution choisie arbitrairement
si j'avais su j'aurais pas venu.
Re: MOOC : Probability from MIT
On cherche alors un réel
A ce stade, on ne SAIT PAS ce que vaut
Ce calcul démontre le résultat intuitif que justement, pour minimiser l'erreur, au sens LMS, il faut choisir a=
Re: MOOC : Probability from MIT
L'idée c'est que si on avait des observations, ce serait seulement 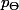 qui changerait, et le réel a qui minimise l'erreur au sens LMS serait donc différent, en prenant en compte les observations.
qui changerait, et le réel a qui minimise l'erreur au sens LMS serait donc différent, en prenant en compte les observations.
65 messages
- Page 4 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
