Méthodes pour valeur approchée d'une intégrale
16 messages
- Page 1 sur 1
Méthodes pour valeur approchée d'une intégrale
Petit à petit, je rajoute des fonctions à une calculette perso pour tout avoir sous la main.
Dernier rajout : la valeur approchée des intégrales.
Je commence par un défit à moi-même : retrouver la formule de Simpson à partir de l'intégration du polynôme interpolateur de Lagrange. Une page de calcul plus tard, formule retrouvée.
(b-a) * [ f(a) + 4 f((a+b)/2) +f(b) ] /6
si on applique ça à un découpage d'un intervalle en n parties identiques, on obtient les coefficients à appliquer pour chaque valuation d'une fonction f (de 0 à n).
(1 4 2 4 2 .... 4 2 4 2 4 1) / 3
à comparer à celle des trapèzes (1 2 2 2 .... 2 2 2 2 1)/2
Là, je me dis, c'est quand même bizarre qu'une simple alternance des coefficients améliore une convergence de 1/n² en 1/n⁴.
Comme je ne trouve pas élégant d'utiliser (1 4 2 4 2 .... 4 2 4 2 4 1) / 3, je pars sur les jolis trapèzes (1 2 2 2 .... 2 2 2 2 1)/2.
Mais, on est en 2018, et chaque méthode est maintenant améliorée comme en IA par une méthode de gradient.
Si la convergence des trapèzes est en 1/n², ça veut dire qui si on fait un calcul avec un découpage en 2n parties, l'erreur est divisée par 4.
Soit : S(2n)-S(n) = 3 * erreur commise sur S(2n)
Le gradient est alors simple à appliquer :
S^= S(2n) + [S(2n)-S(n) ]/3 = [4*S(2n)-S(n) ]/3
Ce résultat a déjà été montré, c'est la méthode de Romberg, cool, du connu.
Pour calculer S(2n) et S(n), on fait 2 fois les même calculs, donc on peut améliorer en ne faisant qu'un seule boucle. Une fois harmonisé ( une valeur sur 2 est divisée par 2n, les autres par n), on retrouve les coefficients suivants à appliquer :
(1 4 2 4 2 .... 4 2 4 2 4 1) / 3
C'est quand même magique de retrouver le même résultat ( avec la convergence qui passe de 1/n² à 1/n⁴) par deux méthodes a priori différentes. L'avantage de la seconde, c'est qu'on voit pourquoi modifier les coefficients marche si bien, c'est en fait une méthode à gradient. La première fournie la majoration de l'erreur.
Et vous, quelle est la méthode que vous préférez pour le calcul d'intégrales ?
Dernier rajout : la valeur approchée des intégrales.
Je commence par un défit à moi-même : retrouver la formule de Simpson à partir de l'intégration du polynôme interpolateur de Lagrange. Une page de calcul plus tard, formule retrouvée.
(b-a) * [ f(a) + 4 f((a+b)/2) +f(b) ] /6
si on applique ça à un découpage d'un intervalle en n parties identiques, on obtient les coefficients à appliquer pour chaque valuation d'une fonction f (de 0 à n).
(1 4 2 4 2 .... 4 2 4 2 4 1) / 3
à comparer à celle des trapèzes (1 2 2 2 .... 2 2 2 2 1)/2
Là, je me dis, c'est quand même bizarre qu'une simple alternance des coefficients améliore une convergence de 1/n² en 1/n⁴.
Comme je ne trouve pas élégant d'utiliser (1 4 2 4 2 .... 4 2 4 2 4 1) / 3, je pars sur les jolis trapèzes (1 2 2 2 .... 2 2 2 2 1)/2.
Mais, on est en 2018, et chaque méthode est maintenant améliorée comme en IA par une méthode de gradient.
Si la convergence des trapèzes est en 1/n², ça veut dire qui si on fait un calcul avec un découpage en 2n parties, l'erreur est divisée par 4.
Soit : S(2n)-S(n) = 3 * erreur commise sur S(2n)
Le gradient est alors simple à appliquer :
S^= S(2n) + [S(2n)-S(n) ]/3 = [4*S(2n)-S(n) ]/3
Ce résultat a déjà été montré, c'est la méthode de Romberg, cool, du connu.
Pour calculer S(2n) et S(n), on fait 2 fois les même calculs, donc on peut améliorer en ne faisant qu'un seule boucle. Une fois harmonisé ( une valeur sur 2 est divisée par 2n, les autres par n), on retrouve les coefficients suivants à appliquer :
(1 4 2 4 2 .... 4 2 4 2 4 1) / 3
C'est quand même magique de retrouver le même résultat ( avec la convergence qui passe de 1/n² à 1/n⁴) par deux méthodes a priori différentes. L'avantage de la seconde, c'est qu'on voit pourquoi modifier les coefficients marche si bien, c'est en fait une méthode à gradient. La première fournie la majoration de l'erreur.
Et vous, quelle est la méthode que vous préférez pour le calcul d'intégrales ?
Re: Méthodes pour valeur approchée d'une intégrale
Salut,
Juste un mot concernant le "méthodes différentes" et le coté "magique" : quelque soit la méthode que tu emploie, si ton but c'est d'obtenir un truc de plus en plus précis lorsque le pas tend vers l'infini, si tu suppose que ta fonction admet localement des D.L., ben ça signifie que ce que tu veut c'est que ta méthode donne la valeur exacte de l'intégrale des premiers termes du D.L. c'est à dire qu'elle donne la valeur exacte sur les polynômes de degrés <= à une valeur donnée.
Et comme le truc à approximer, à savoir l'intégrale, est linéaire en la fonction f à intégrer et que les trucs avec lesquels tu approxime, à savoir les f(x_i) sont eux aussi linéaires, ben le problème revient à un bête système linéaire à résoudre vu qu'il suffit que ça marche sur une base de l'espace des polynômes de degré <= ?.
Et comme en plus dans l'intégrale on peut faire des changement de variable (affine) pour se ramener à un même intervalle "de base", si on veut utiliser f(a), f(b) et f((a+b)/2), le problème se résume entièrement à la recherche des coeff.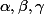 tels que
tels que \,dx\!=\!\alpha P(-1)\!+\!\beta P(0)\!+\!\gamma P(1)) pour
pour 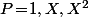 c'est à dire
c'est à dire 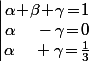 avec le "coup de pot" (lié à la parité) que ça marchera encore pour
avec le "coup de pot" (lié à la parité) que ça marchera encore pour 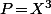 vu que de nouveau l'équation est
vu que de nouveau l'équation est 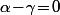 comme pour
comme pour 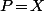 .
.
Sinon, concernant la dernière question, si c'est pour du calcule "réel" où c'est effectivement le résultat approximatif qui m’intéresse, et s'il est clair que la fonction est suffisamment régulière, c'est plutôt Romberg que j'utiliserais (mais faire gaffe à bien vérifier que les coeff. du D.L. ne deviennent pas rapidement super grand vu que dans ce cas, ça déconne complètement et ça peut même rendre la méthode divergente).
Par contre, concernant le point de vue plus théorique, j'ai toujours trouvé très joli le fait de chercher non seulement quels coeff. mettre avec des points imposés (comme çi dessus avec une subdivision régulière de 3 points), mais aussi de chercher où placer les points de façon à ce que ça approxime au mieux. Par exemple, avec 3 points, quelles sont les valeurs de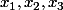 à choisir de façon à ce que le système
à choisir de façon à ce que le système \,dx\!=\!\alpha P(x_1)\!+\!\beta P(x_2)\!+\!\gamma P(x_3)) avec
avec 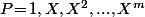 ait des solutions en
ait des solutions en 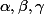 pour
pour  le plus grand possible.
le plus grand possible.
Juste un mot concernant le "méthodes différentes" et le coté "magique" : quelque soit la méthode que tu emploie, si ton but c'est d'obtenir un truc de plus en plus précis lorsque le pas tend vers l'infini, si tu suppose que ta fonction admet localement des D.L., ben ça signifie que ce que tu veut c'est que ta méthode donne la valeur exacte de l'intégrale des premiers termes du D.L. c'est à dire qu'elle donne la valeur exacte sur les polynômes de degrés <= à une valeur donnée.
Et comme le truc à approximer, à savoir l'intégrale, est linéaire en la fonction f à intégrer et que les trucs avec lesquels tu approxime, à savoir les f(x_i) sont eux aussi linéaires, ben le problème revient à un bête système linéaire à résoudre vu qu'il suffit que ça marche sur une base de l'espace des polynômes de degré <= ?.
Et comme en plus dans l'intégrale on peut faire des changement de variable (affine) pour se ramener à un même intervalle "de base", si on veut utiliser f(a), f(b) et f((a+b)/2), le problème se résume entièrement à la recherche des coeff.
Sinon, concernant la dernière question, si c'est pour du calcule "réel" où c'est effectivement le résultat approximatif qui m’intéresse, et s'il est clair que la fonction est suffisamment régulière, c'est plutôt Romberg que j'utiliserais (mais faire gaffe à bien vérifier que les coeff. du D.L. ne deviennent pas rapidement super grand vu que dans ce cas, ça déconne complètement et ça peut même rendre la méthode divergente).
Par contre, concernant le point de vue plus théorique, j'ai toujours trouvé très joli le fait de chercher non seulement quels coeff. mettre avec des points imposés (comme çi dessus avec une subdivision régulière de 3 points), mais aussi de chercher où placer les points de façon à ce que ça approxime au mieux. Par exemple, avec 3 points, quelles sont les valeurs de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Méthodes pour valeur approchée d'une intégrale
@Ben Par curiosité, ce sont les abscisses de Tchebychev qu'on va trouver?
Re: Méthodes pour valeur approchée d'une intégrale
Bonjour
Je ne suis pas trop d'accord avec la forme de la question de ce post : "Et vous, quelle est la méthode que vous préférez pour le calcul d'intégrales" ?
En effet, le principe du calcul numérique consiste à trouver des valeurs approchées des solutions de problèmes qu'on ne sait pas résoudre exactement. Chaque problème est spécifique et à ma connaissance il n'y a pas UNE méthode qui va l'emporter sur les autres.
En particulier dans le calcul intégral ce n'est pas les méthodes de Newton-Cotes ( Trapèzes, Simpson et l'accélération de Romberg) qui peut avoir une préférence par rapport à d'autres méthodes.
Par exemple les mécaniciens utilisent beaucoup les points de Gauss (je ne sais pas trop pourquoi mais c'est un fait).
Pour comprendre mon propos soit cette intégrale}} dx)
Est ce que la méthode de Simpson est adaptée au calcul de I?
Alors peut on dire que "la méthode de Simpson est celle que l'on préfère pour le calcul d'intégrales".
Je ne suis pas trop d'accord avec la forme de la question de ce post : "Et vous, quelle est la méthode que vous préférez pour le calcul d'intégrales" ?
En effet, le principe du calcul numérique consiste à trouver des valeurs approchées des solutions de problèmes qu'on ne sait pas résoudre exactement. Chaque problème est spécifique et à ma connaissance il n'y a pas UNE méthode qui va l'emporter sur les autres.
En particulier dans le calcul intégral ce n'est pas les méthodes de Newton-Cotes ( Trapèzes, Simpson et l'accélération de Romberg) qui peut avoir une préférence par rapport à d'autres méthodes.
Par exemple les mécaniciens utilisent beaucoup les points de Gauss (je ne sais pas trop pourquoi mais c'est un fait).
Pour comprendre mon propos soit cette intégrale
Est ce que la méthode de Simpson est adaptée au calcul de I?
Alors peut on dire que "la méthode de Simpson est celle que l'on préfère pour le calcul d'intégrales".
Re: Méthodes pour valeur approchée d'une intégrale
Quand c'est une intégrale généralisée, toute méthode doit y être adaptée car sa définition passe par une limite.
1/√x pose le même problème, et son intégrale entre 0 et 1 est connue
elle garde le même signe au voisinage de 0
si j'ignore la première valeur, j'ai bien une approximation (grossière) de la valeur
On peut décider de modifier le pas de façon récursive en fonction des variations de la fonction (gestion de l'erreur) et d'y rajouter une convergence .
En tout cas ça me donne des idées pour la prochaine version.
1/√x pose le même problème, et son intégrale entre 0 et 1 est connue
elle garde le même signe au voisinage de 0
si j'ignore la première valeur, j'ai bien une approximation (grossière) de la valeur
On peut décider de modifier le pas de façon récursive en fonction des variations de la fonction (gestion de l'erreur) et d'y rajouter une convergence .
En tout cas ça me donne des idées pour la prochaine version.
Re: Méthodes pour valeur approchée d'une intégrale
Oui, c'est ça.LB2 a écrit:@Ben Par curiosité, ce sont les abscisses de Tchebychev qu'on va trouver?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Méthodes pour valeur approchée d'une intégrale
J'ai fait quelques recherches, et certains cours m'ont bien fait rire.
Certains partent de polynômes orthogonaux où par magie une fonction de pondération pas encore définie apparaît dans le produit scalaire pour finir par être celle recherchée.
Le résultat de la recherche est parfois très joli : en recherchant un polynôme qui s'approche d'un polynôme, on trouve un polynôme (perso, je n'ai pas trop de difficulté à trouver une primitive de polynôme).
C'est joli, mais intellectuellement inconsistant.
Le fond du problème n'est jamais vraiment abordé : un polynôme défini en n points façon polynôme interpolateur est un très mauvais candidat à cause du problème de Runge :
https://fr.wikipedia.org/wiki/Ph%C3%A9n ... e_de_Runge
C'est qui est beau là dedans, c'est qu'une simple fonction 1 /(1+25x²) que l'on peut classer "assez lisse, bornée, continue, sympa" est un contre exemple de vouloir expliquer des choses avec des polynômes. Au passage, les méthodes basiques d'intégration sur un compact marchent très bien sur cette fonction.
Mais, Tchebychev a de bons résultats, les démos qui passent par les polynômes interpolateurs sont avant tout des calculs qui cherchent des solutions dans un cas a priori non généralisable mais qui sont beaucoup plus généralistes. Les polynômes de Legendre paraissent, vu de loin, une base plus sympa à utiliser.
Comme en gros, le mieux c'est de ne pas utiliser un degré trop haut et des points et coefs déjà calculés, ça fini en queue de poisson.
J'ai vu apparaître dans un cours sur de l'intégration sur un compact sur un panel de fonctions tests, pour des réels avec 17 chiffres de précision :
-> les méthodes des rectangles et trapèzes saturent du fait des erreurs d'arrondis dés n= 1000 000 et arrivent rarement à plus de 12 chiffres de précision.
-> Simpson permet avec n=1000 d'avoir un bien meilleur compromis avec 14 chiffres de précision.
-> Gauss Legendre donne le même genre de résultat pour n= 7....(oui, ça fait mal, c'est là qu'on se dit que cette histoire de polynôme interpolateur par laquelle on passe qui se doit de ne pas marcher mérite des démos bien mieux faites).
-> Et pourquoi pas un simple Romberg itératif qui marche lui aussi très bien et reste dans le cadre de départ : une méthode améliorée à gradient.
PS] cf sujet Cachan 2016 pour Legendre :
http://www.iecl.univ-lorraine.fr/~Olivier.Garet/annales-cachan/cachan2016_IIB.pdf
Certains partent de polynômes orthogonaux où par magie une fonction de pondération pas encore définie apparaît dans le produit scalaire pour finir par être celle recherchée.
Le résultat de la recherche est parfois très joli : en recherchant un polynôme qui s'approche d'un polynôme, on trouve un polynôme (perso, je n'ai pas trop de difficulté à trouver une primitive de polynôme).
C'est joli, mais intellectuellement inconsistant.
Le fond du problème n'est jamais vraiment abordé : un polynôme défini en n points façon polynôme interpolateur est un très mauvais candidat à cause du problème de Runge :
https://fr.wikipedia.org/wiki/Ph%C3%A9n ... e_de_Runge
C'est qui est beau là dedans, c'est qu'une simple fonction 1 /(1+25x²) que l'on peut classer "assez lisse, bornée, continue, sympa" est un contre exemple de vouloir expliquer des choses avec des polynômes. Au passage, les méthodes basiques d'intégration sur un compact marchent très bien sur cette fonction.
Mais, Tchebychev a de bons résultats, les démos qui passent par les polynômes interpolateurs sont avant tout des calculs qui cherchent des solutions dans un cas a priori non généralisable mais qui sont beaucoup plus généralistes. Les polynômes de Legendre paraissent, vu de loin, une base plus sympa à utiliser.
Comme en gros, le mieux c'est de ne pas utiliser un degré trop haut et des points et coefs déjà calculés, ça fini en queue de poisson.
J'ai vu apparaître dans un cours sur de l'intégration sur un compact sur un panel de fonctions tests, pour des réels avec 17 chiffres de précision :
-> les méthodes des rectangles et trapèzes saturent du fait des erreurs d'arrondis dés n= 1000 000 et arrivent rarement à plus de 12 chiffres de précision.
-> Simpson permet avec n=1000 d'avoir un bien meilleur compromis avec 14 chiffres de précision.
-> Gauss Legendre donne le même genre de résultat pour n= 7....(oui, ça fait mal, c'est là qu'on se dit que cette histoire de polynôme interpolateur par laquelle on passe qui se doit de ne pas marcher mérite des démos bien mieux faites).
-> Et pourquoi pas un simple Romberg itératif qui marche lui aussi très bien et reste dans le cadre de départ : une méthode améliorée à gradient.
PS] cf sujet Cachan 2016 pour Legendre :
http://www.iecl.univ-lorraine.fr/~Olivier.Garet/annales-cachan/cachan2016_IIB.pdf
Re: Méthodes pour valeur approchée d'une intégrale
Bonjour
Ton discours sur les différentes méthodes n'est pas bien clair. Tu emploies souvent des tournures de phrases qui te sont propres mais pas très explicites (pour moi au moins) donc que dire vraiment?
Concernant la théorie des polynômes orthogonaux qui est à la base de l'intégration Gaussienne, oui effectivement c'est joli, mais je ne peux pas accepter que tu dises que c'est intellectuellement inconsistant.
Dire que le fond du problème n'est jamais abordé c'est complètement faux (sauf peut-être dans les cours que tu as utilisés). La théorie est très bien ficelée depuis longtemps et la gestion de l'erreur
due à l'intégration numérique est très bien connue.
Du point de vue théorique, il n'y a pas différence entre les différentes méthodes de Gauss (Gauss-Legendre, Gauss-Hermite ou Gauss-Tchebychev), c'est pour cela que par mesure d'économie on se place dans un cadre général avec une certaine fonction poids non explicitée au départ.
Concernant le phénomène de Runge il n'apparait pas uniquement dans la méthode de Gauss, il apparait aussi dans les méthodes de Newton-Cotes dont fait partie la méthode de Simpson.
Je le répète, en analyse numérique, il n'y a pas une méthode qui l'emporte par rapport à une autre. Tout dépend du problème que l'on a à traiter.
On a l'impression que tu veux expliquer que la panacée c'est la méthode des trapèzes que l'on accélère avec la méthode de Romberg. Mais c'est faux, en mécanique je sais que les points de Gauss sont très utilisés et ce n'est surement pas pour rien. Voir par exemple le lien ci-dessous.
https://www.emse.fr/~drapier/index_fichiers/CoursPDF/Meca-Num3A/Methodes-Num-2015.pdf
Ton discours sur les différentes méthodes n'est pas bien clair. Tu emploies souvent des tournures de phrases qui te sont propres mais pas très explicites (pour moi au moins) donc que dire vraiment?
Concernant la théorie des polynômes orthogonaux qui est à la base de l'intégration Gaussienne, oui effectivement c'est joli, mais je ne peux pas accepter que tu dises que c'est intellectuellement inconsistant.
Dire que le fond du problème n'est jamais abordé c'est complètement faux (sauf peut-être dans les cours que tu as utilisés). La théorie est très bien ficelée depuis longtemps et la gestion de l'erreur
due à l'intégration numérique est très bien connue.
Du point de vue théorique, il n'y a pas différence entre les différentes méthodes de Gauss (Gauss-Legendre, Gauss-Hermite ou Gauss-Tchebychev), c'est pour cela que par mesure d'économie on se place dans un cadre général avec une certaine fonction poids non explicitée au départ.
Concernant le phénomène de Runge il n'apparait pas uniquement dans la méthode de Gauss, il apparait aussi dans les méthodes de Newton-Cotes dont fait partie la méthode de Simpson.
Je le répète, en analyse numérique, il n'y a pas une méthode qui l'emporte par rapport à une autre. Tout dépend du problème que l'on a à traiter.
On a l'impression que tu veux expliquer que la panacée c'est la méthode des trapèzes que l'on accélère avec la méthode de Romberg. Mais c'est faux, en mécanique je sais que les points de Gauss sont très utilisés et ce n'est surement pas pour rien. Voir par exemple le lien ci-dessous.
https://www.emse.fr/~drapier/index_fichiers/CoursPDF/Meca-Num3A/Methodes-Num-2015.pdf
Re: Méthodes pour valeur approchée d'une intégrale
On se focalise sur l'ordre de la quadrature et on dit que si deux fonctions passent par n points, leurs intégrales sont identiques.
En soit pour n= 1000 sur [-1;1], c'est normal de confondre deux fonctions
Mais là, on est plutôt du genre n=10 sur [-1;1], entre quand on se base sur un polynôme qui passe par 10 points imposés, il ne ressemble pas forcément à la fonction qu'on veut évaluer. C'est presque anormal d'avoir une aussi bonne convergence.
C'est là que je me dis que le calcul qu'on fait est juste, mais n'est pas la preuve qui dit qu'on fait bien l'évaluation de l'intégrale.
Je vais me pencher sur Stone-Weierstrass qui part bien de Tchebychev et utilise la bonne norme de mesure.
En soit pour n= 1000 sur [-1;1], c'est normal de confondre deux fonctions
Mais là, on est plutôt du genre n=10 sur [-1;1], entre quand on se base sur un polynôme qui passe par 10 points imposés, il ne ressemble pas forcément à la fonction qu'on veut évaluer. C'est presque anormal d'avoir une aussi bonne convergence.
C'est là que je me dis que le calcul qu'on fait est juste, mais n'est pas la preuve qui dit qu'on fait bien l'évaluation de l'intégrale.
Je vais me pencher sur Stone-Weierstrass qui part bien de Tchebychev et utilise la bonne norme de mesure.
Re: Méthodes pour valeur approchée d'une intégrale
Je suis aller un peu plus loin : l'approximation de Bernstein.
La démo est hallucinante mais la convergence très lente.
Le gros+ : elle part de la norme infinie, ce qui est un bon critère.
Le gros - : les démos de convergence se basent sur la majoration de l'accroissement entre deux abscisses équidistantes. C'est suffisant pour la démo, mais pas du tout généralisable (du genre racine(x) devient une fonction dont on devrait choisir un pas très fin alors que la réalité dit le contraire).
Je reste donc toujours un peu sur ma faim.
D'un coté, des méthodes qui marchent très bien mais dont la convergence comme intégrale sur une "vraie" fonction reste très vague.
De l'autre, des existences de familles convergentes, donc celles qu'on explicitent ont des convergences très lentes.
Pour ce qui est de la norme infinie ; c'est un critère pas si bon que ça : 1 +sin(156543516355x) sur [0;100] et f(x)=1 sont loin l'une de l'autre pour la norme infinie, mais pas leur intégrale.
Mais tj pas de démo qui vont chercher à minimiser le phénomène de Runge en faisant que ses effets s'annulent sur de domaine d'intégration par exemple.
La démo est hallucinante mais la convergence très lente.
Le gros+ : elle part de la norme infinie, ce qui est un bon critère.
Le gros - : les démos de convergence se basent sur la majoration de l'accroissement entre deux abscisses équidistantes. C'est suffisant pour la démo, mais pas du tout généralisable (du genre racine(x) devient une fonction dont on devrait choisir un pas très fin alors que la réalité dit le contraire).
Je reste donc toujours un peu sur ma faim.
D'un coté, des méthodes qui marchent très bien mais dont la convergence comme intégrale sur une "vraie" fonction reste très vague.
De l'autre, des existences de familles convergentes, donc celles qu'on explicitent ont des convergences très lentes.
Pour ce qui est de la norme infinie ; c'est un critère pas si bon que ça : 1 +sin(156543516355x) sur [0;100] et f(x)=1 sont loin l'une de l'autre pour la norme infinie, mais pas leur intégrale.
Mais tj pas de démo qui vont chercher à minimiser le phénomène de Runge en faisant que ses effets s'annulent sur de domaine d'intégration par exemple.
Re: Méthodes pour valeur approchée d'une intégrale
Le problème à mon avis, c'est que tant que tu ne précise pas sur quelle classe de fonction tu veut que ta méthode "marche bien", ben ça a pas de sens de se poser la question.
- Sur des fonction "hyper régulière", c'est à dire développable en série entière avec un rayon de C.V. infini (*) là, je pense qu'il y a pas photo : numériquement parlant, Romberg doit être "imbattable".
- Mais dés que tu t'éloigne un tant soit peu de ce cas "optimal", Romberg pose plus que de gros problème vu que sa "grande vitesse" qui est liée à un calcul exact sur les polynômes jusqu'à un grand degrés, ben d'un autre coté, ce que ça te dit, c'est que la vitesse de C.V. est lié à la valeur Max. des dérivées n-ièmes avec n très grand de la fonction que tu intègre. Et si ces dérivées n-ièmes explosent, ben c'est la cata. : la "soit disant amélioration" produite par la méthode peut au contraire aller jusqu'à provoquer la divergence de la méthode.
- D'un autre coté, si tu veut une méthode qui marche bien pour une classe très générale de fonction (du style toutes les fonctions continue et rien de plus) alors tu fera rien de mieux que la méthode des rectangles ou les trapèzes : tout le reste risque de beaucoup moins bien converger (et demander bien plus de calculs).
Donc par exemple pas avec la fonction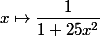 vu qu'elle a un pôle en
vu qu'elle a un pôle en 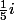 et que, bien que ce pole soit complexe (non réel), ben il influe plus que grandement sur le comportement de la fonction. En particulier, c'est lui qui fait que, même vue comme fonction "purement" de R->R, ben les développement en série entière n'ont pas un rayon de c.v. infini (et donc les D.L. ne convergent pas de façon optimale)
et que, bien que ce pole soit complexe (non réel), ben il influe plus que grandement sur le comportement de la fonction. En particulier, c'est lui qui fait que, même vue comme fonction "purement" de R->R, ben les développement en série entière n'ont pas un rayon de c.v. infini (et donc les D.L. ne convergent pas de façon optimale)
- Sur des fonction "hyper régulière", c'est à dire développable en série entière avec un rayon de C.V. infini (*) là, je pense qu'il y a pas photo : numériquement parlant, Romberg doit être "imbattable".
- Mais dés que tu t'éloigne un tant soit peu de ce cas "optimal", Romberg pose plus que de gros problème vu que sa "grande vitesse" qui est liée à un calcul exact sur les polynômes jusqu'à un grand degrés, ben d'un autre coté, ce que ça te dit, c'est que la vitesse de C.V. est lié à la valeur Max. des dérivées n-ièmes avec n très grand de la fonction que tu intègre. Et si ces dérivées n-ièmes explosent, ben c'est la cata. : la "soit disant amélioration" produite par la méthode peut au contraire aller jusqu'à provoquer la divergence de la méthode.
- D'un autre coté, si tu veut une méthode qui marche bien pour une classe très générale de fonction (du style toutes les fonctions continue et rien de plus) alors tu fera rien de mieux que la méthode des rectangles ou les trapèzes : tout le reste risque de beaucoup moins bien converger (et demander bien plus de calculs).
Donc par exemple pas avec la fonction
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Méthodes pour valeur approchée d'une intégrale
On peut se dire que sont intégrables :
cas 1 : continues sur un compact, dont le nombre de points singuliers (dérivée infinie ou non définie à un certain ordre) et au plus infini dénombrable. (par somme, on a les continues par morceaux)
cas 2 : même chose mais sur un intervalle
Je pense que des travaux plus poussés on été fait, mais que le résultat dépend de chaque type de fonction ou du domaine d’application. Le tout vérifié par un panel de fonction test.
J'ai ressorti ma fx850p de 1990, elle utilise Romberg et on pouvait choisir soit le calcul classique, soit le choix de l'erreur, par contre, plantage complet sur du 1/racine(x)
pour Aviateur
en 0 :
}} dx)
=
}} -\frac{1}{\sqrt{x}} + \frac{1}{\sqrt{x}} dx)
= 1.20378 ... ?
= 1.2037827 avec 100 itérations en 3 points
= 1.2037823 avec 10 itérations en 15 points
= 1.2037817 avec 1000 itérations trapèze accéléré 1 fois
en 0.5, on a une divergence type "1/x" du "1/ [(pi/2) *(0.5-t)] " plus exactement
cas 1 : continues sur un compact, dont le nombre de points singuliers (dérivée infinie ou non définie à un certain ordre) et au plus infini dénombrable. (par somme, on a les continues par morceaux)
cas 2 : même chose mais sur un intervalle
Je pense que des travaux plus poussés on été fait, mais que le résultat dépend de chaque type de fonction ou du domaine d’application. Le tout vérifié par un panel de fonction test.
J'ai ressorti ma fx850p de 1990, elle utilise Romberg et on pouvait choisir soit le calcul classique, soit le choix de l'erreur, par contre, plantage complet sur du 1/racine(x)
pour Aviateur
en 0 :
=
= 1.20378 ... ?
= 1.2037827 avec 100 itérations en 3 points
= 1.2037823 avec 10 itérations en 15 points
= 1.2037817 avec 1000 itérations trapèze accéléré 1 fois
en 0.5, on a une divergence type "1/x" du "1/ [(pi/2) *(0.5-t)] " plus exactement
Modifié en dernier par pascal16 le 19 Déc 2018, 09:21, modifié 4 fois.
Re: Méthodes pour valeur approchée d'une intégrale
Un gars qui a déjà regardé quand les oscillations de Runge arrivaient :http://www.lavrovo.fr/Arithmurgistan/Interpolation/lagrange.html
points équidistants, sur une fonction pas sympa : dès un degré n= 6
points et poids choisis via Tchebychev : RAS même à n=60
points équidistants, sur une fonction pas sympa : dès un degré n= 6
points et poids choisis via Tchebychev : RAS même à n=60
Modifié en dernier par pascal16 le 15 Déc 2018, 17:21, modifié 1 fois.
Re: Méthodes pour valeur approchée d'une intégrale
Bonjour,
de nombreux sujets de concours s'intéressent au phénomène de Runge et aux polynômes d'interpolation.
Par exemple, HEC ECS 2017 (Bernstein, Lagrange et phénomène de Runge)
de nombreux sujets de concours s'intéressent au phénomène de Runge et aux polynômes d'interpolation.
Par exemple, HEC ECS 2017 (Bernstein, Lagrange et phénomène de Runge)
Re: Méthodes pour valeur approchée d'une intégrale
4h de math calculatoire sans calculette pour faire HEC, fo du courage. Le sujet est très détaillé, mais il donne pas vraiment envie.
Ensuite, pour les intégrales généralisées en un point ou en +oo il y a un truc ?
en un point : "f- un équivalent calculable à la main" marche, mais c'est pas automatisé.
Ensuite, pour les intégrales généralisées en un point ou en +oo il y a un truc ?
en un point : "f- un équivalent calculable à la main" marche, mais c'est pas automatisé.
Re: Méthodes pour valeur approchée d'une intégrale
Ce WE, j'ai codé un peu et cherché des sources
Je passe par Gauss-Tchebychev, je code sur [-1;1], mais ça ne passe pas ma phase de test. Surestimation et vitesse de convergence douteuse, je revérifie tout, met des 2.0 à la place des 2 pour éviter les problèmes de division entière etc... galère totale. Je test des méthode modifiées, mais rien à faire, il y a un truc qui ne marche pas.
Sur wiki, y a Gauss-Kronrod (coef+ poids) pour n=15, je code ça en 5 minutes sur [-1;1], test polynômes : trop bon et fn ok, Je modifie sur [a;b] et hop du 10^-16 de précision du premier coup.
Je teste un Gauss-Legendre avec seulement 3 points + découpage en 100 de l’intervalle : trop bon comme résultats.
je regarde un peu sur internet les sources de quadrature de Gauss.
Là, je tombe sur le sources de QUADPACK pour Fortran77 le tout écrit entre 1981 et 1983.
Le fortran, c'est un peu lourd à suivre car toute variable est globale, donc, il faut systématiquement revenir à la dernière occurrence qui l'a modifiée et il faut suivre les sauts.
Finalement, il y avait à l'époque l'ago complet qui inclus tout ce dont on a besoin.
je résume grossièrement le fonctionnement :
soit f définie sur [a,b], à intégrer sur une portion [l,r]
si l n'est pas a et r n'est pas b sont loin, je suppose f régulière, je fais un Gauss-X à n et 2n points où X est un méthode où les points "n" et "2n" coïncident (Kronrod par ex), l'erreur retournée est la différence entre les deux calculs et la valeur, le calcul en 2n.
si on est en a, Gauss-Tchebychev à 12 et 24 points, mais avec la modif de f en f(x)*(x-a)^alpha, il y a une routine qui donne les nouveaux coefs à appliquer, on retourne l'erreur
si on est en b, Gauss-Tchebychev à 12 et 24 points, mais avec la modif de f en f(x)*(b-x)^beta, il y a une routine qui donne les nouveaux coefs à appliquer on retourne l'erreur
si a=oo ou b=oo, il y a une autre routine qui marche avec un développement en exp(-x)
de plus, il y a une fonction norme infinie qui permet de déterminer si f est régulière en a et b.
au final, on somme les morceaux, avec itération possible si on travaille si on veut sur l'erreur cumulée.
Un sous programme donne les poids et abscisses de Gauss-X
Comme l'intégration choisie a été [l,r] et pas [-1;1], on "passe" comme argument
a,b,l,r,alpha,beta, les vecteurs position et poids, le type d'intégration.
en retour : "a,b,l,r,alpha,beta, le type d'intégration" ne sont pas modifiés
: le vecteur position et les vecteurs poids sont renvoyé pour tous chaque types d'intégration.
Les calculs sont touts des récurrences pas très longues.
les source fortran : http://www.netlib.org/quadpack/
dqc25c.f est la première où j'ai vu cet algo, elle demande certaines autres sources comme dqmomo.f qui recalcule tous les poids.
Voilà, Aviateur, il suffisait d'être universitaire dans les années 80.
Je passe par Gauss-Tchebychev, je code sur [-1;1], mais ça ne passe pas ma phase de test. Surestimation et vitesse de convergence douteuse, je revérifie tout, met des 2.0 à la place des 2 pour éviter les problèmes de division entière etc... galère totale. Je test des méthode modifiées, mais rien à faire, il y a un truc qui ne marche pas.
Sur wiki, y a Gauss-Kronrod (coef+ poids) pour n=15, je code ça en 5 minutes sur [-1;1], test polynômes : trop bon et fn ok, Je modifie sur [a;b] et hop du 10^-16 de précision du premier coup.
Je teste un Gauss-Legendre avec seulement 3 points + découpage en 100 de l’intervalle : trop bon comme résultats.
je regarde un peu sur internet les sources de quadrature de Gauss.
Là, je tombe sur le sources de QUADPACK pour Fortran77 le tout écrit entre 1981 et 1983.
Le fortran, c'est un peu lourd à suivre car toute variable est globale, donc, il faut systématiquement revenir à la dernière occurrence qui l'a modifiée et il faut suivre les sauts.
Finalement, il y avait à l'époque l'ago complet qui inclus tout ce dont on a besoin.
je résume grossièrement le fonctionnement :
soit f définie sur [a,b], à intégrer sur une portion [l,r]
si l n'est pas a et r n'est pas b sont loin, je suppose f régulière, je fais un Gauss-X à n et 2n points où X est un méthode où les points "n" et "2n" coïncident (Kronrod par ex), l'erreur retournée est la différence entre les deux calculs et la valeur, le calcul en 2n.
si on est en a, Gauss-Tchebychev à 12 et 24 points, mais avec la modif de f en f(x)*(x-a)^alpha, il y a une routine qui donne les nouveaux coefs à appliquer, on retourne l'erreur
si on est en b, Gauss-Tchebychev à 12 et 24 points, mais avec la modif de f en f(x)*(b-x)^beta, il y a une routine qui donne les nouveaux coefs à appliquer on retourne l'erreur
si a=oo ou b=oo, il y a une autre routine qui marche avec un développement en exp(-x)
de plus, il y a une fonction norme infinie qui permet de déterminer si f est régulière en a et b.
au final, on somme les morceaux, avec itération possible si on travaille si on veut sur l'erreur cumulée.
Un sous programme donne les poids et abscisses de Gauss-X
Comme l'intégration choisie a été [l,r] et pas [-1;1], on "passe" comme argument
a,b,l,r,alpha,beta, les vecteurs position et poids, le type d'intégration.
en retour : "a,b,l,r,alpha,beta, le type d'intégration" ne sont pas modifiés
: le vecteur position et les vecteurs poids sont renvoyé pour tous chaque types d'intégration.
Les calculs sont touts des récurrences pas très longues.
les source fortran : http://www.netlib.org/quadpack/
dqc25c.f est la première où j'ai vu cet algo, elle demande certaines autres sources comme dqmomo.f qui recalcule tous les poids.
Voilà, Aviateur, il suffisait d'être universitaire dans les années 80.
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
