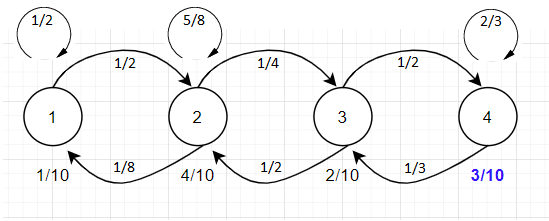
Supposons que l'on vous donne une chaîne de Markov en temps discret composée des états 1, 2, 3 et 4 disposés dans une chaîne linéaire. Les probabilités d'être dans l'état 1 sont de 1/10, dans l'état 2 de 4/10 et dans l'état 3 de 2/10. Les transitions autorisées sont de 1 à 2 (et retour), de 2 à 3 et retour et de 3 à 4 et retour.
1 - Représentez graphiquement cette chaîne de Markov en utilisant des flèches pour indiquer les transitions d'état autorisées.
2 - Étiquetez les flèches avec les probabilités de transition qui réalisent les probabilités de l'état stable (steady state probability). Ecrivez les probabilités de transitions sous forme de fractions.
Utilisez la formule de Metropolis pour les calculer. Sous la visualisation du graphique, écrivez explicitement la formule que vous avez utilisée pour calculer la probabilité de transition de l'état 4 à l'état 3.
Afin de trouver la probabilité de transition j'ai appliquer la méthode de mon cours que voici:

Calcul de l'acceptance :
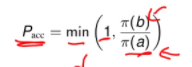
(Je sais que steady state probability représente les probabilités d'un état après un grands nombres d'itérations. Je sais comment le calculer avec l'algorythme Metropolis mais ce n'est pas ce qui est demandé ici.)
1 - Voici mon graph:
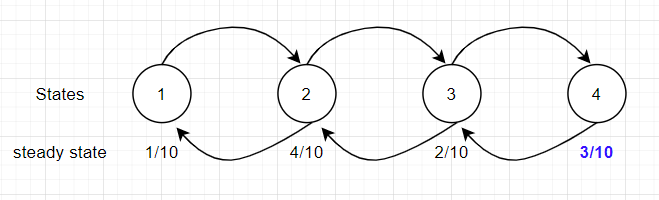
J'ai rajouté la steady state probability pour l'état 4 qui est selon moi de 3/10. Est-ce correct ?
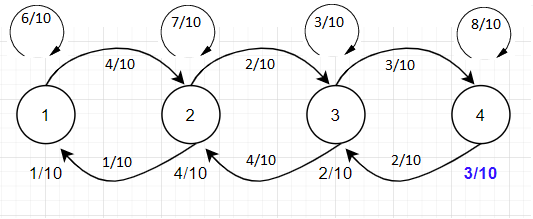
2 - J'ai essayer de calculer les probabilitées de transitions entre les états 1 => 2 et 2 => 1 (en suivant la méthode en screenshot):
J'ai calculer les acceptances pour les transitions entre états:
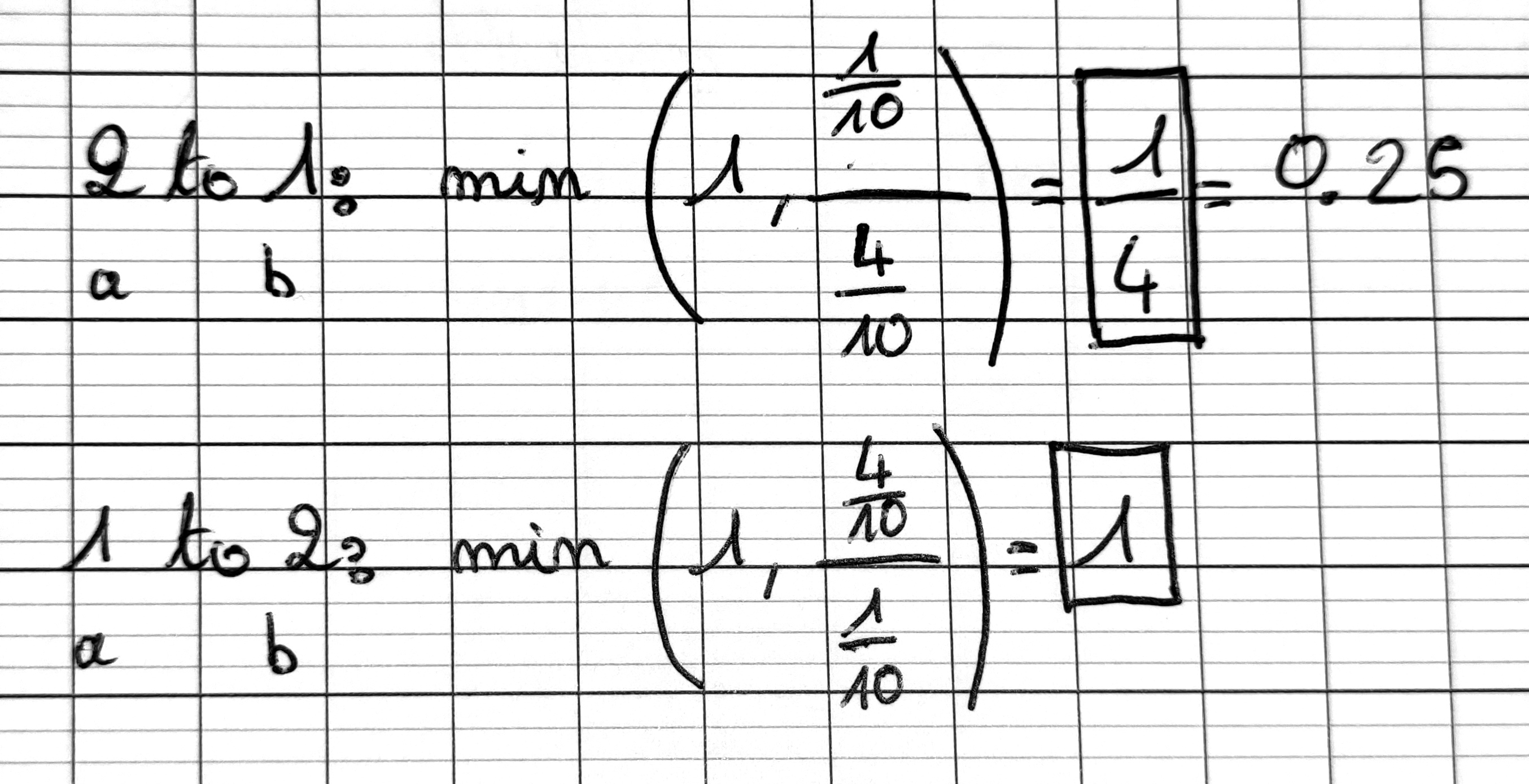
Je ne comprends cependant pas le point numéro 2 de la méthode. Pourriez-vous me l'expliquer ou me mettre sur la voie ?
Merci pour votre aide et bonne journée