Pour résoudre l'inéquation
Les inéquations
32 messages
- Page 1 sur 2 - 1, 2
Les inéquations
Bonsoir!
Pour résoudre l'inéquation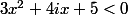 , où
, où 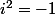 .
.
Pour résoudre l'inéquation
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Dacu a écrit:Non , si.Autre chose?!
Salut, les complexes ne sont pas un ensemble ordonné donc i>1 n'a pas de sens (tu ne peux pas comparer des complexes et des réels ou des complexes avec d'autres complexes, seulement les réels avec les réels). Donc si tu veux résoudre ton inéquation sous quelle forme doit nécessairement être x ?
Edit : pardon je n'avais pas fais attention tu l'as déjà dit, autant pour moi.
Archytas a écrit:Salut, les complexes ne sont pas un ensemble ordonné donc i>1 n'a pas de sens (tu ne peux pas comparer des complexes et des réels ou des complexes avec d'autres complexes, seulement les réels avec les réels). Donc si tu veux résoudre ton inéquation sous quelle forme doit nécessairement être x ?
Edit : pardon je n'avais pas fais attention tu l'as déjà dit, autant pour moi.
Salut!Pas de problème!Comment résoudre l'inéquation
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Dacu a écrit:Salut!Pas de problème!Comment résoudre l'inéquationoù
?
Pour que ton inéquation ait un sens il faut que la partie de gauche de ton inéquation soit réelle sans quoi tu ne pourras pas comparer, donc x doit nécessairement être imaginaire pur c'est à dire x s'écrit de la forme x=i.y avec y un réel. Il te suffit de remplacer x par cette valeur et de résoudre l'inéquation de manière classique comme pour les réels (= !
Le_chat a écrit:Cette inéquation n'a pas trop de sens si tu dis que x est un élément de R ou C, vu que tu ne définis pas ce que tu entends par "un complexe est < à un autre". A la rigueur si tu fixes la condition x imaginaire pur on va pouvoir le résoudre étant donné que le membre de gauche sera réel.
En conclusion, quelles sont les solutions d'inéquation ?
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Archytas a écrit:Pour que ton inéquation ait un sens il faut que la partie de gauche de ton inéquation soit réelle sans quoi tu ne pourras pas comparer, donc x doit nécessairement être imaginaire pur c'est à dire x s'écrit de la forme x=i.y avec y un réel. Il te suffit de remplacer x par cette valeur et de résoudre l'inéquation de manière classique comme pour les réels (= !
Détail, s'il vous plaît !J'ai pensé autrement.
Nous pouvons écrire que
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Dacu a écrit:Détail, s'il vous plaît !J'ai pensé autrement.
Nous pouvons écrire queoù
et
. Résoudre cette équation, nous trouvons les solutions d'inéquation.Je crois que mon raisonnement est correct.
Oui mais le principe est le même x doit toujours être imaginaire pur car a<0 ce qui nous indique que a est réel. Pour t'en concaincre on va résoudre
Pour en rajouter une couche : ce genre d'inéquation n'a pas vraiment de sens...
Soit tu cherches : les x tel que ton polynome soit réel et que tu aies l'inégalité voulue,
soit tu définie l'ordre que tu veux voir vérifié sur C.
Soit tu cherches : les x tel que ton polynome soit réel et que tu aies l'inégalité voulue,
soit tu définie l'ordre que tu veux voir vérifié sur C.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Archytas a écrit:Encore une fois pose x=iy.
Bonjour!
S'il vous plaît continuer votre raisonnement,parce que je ne sais pas vraiment comment résoudre l'inéquation résultant en rendant la substitution
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
[quote="Dacu"]Bonjour!
S'il vous plaît continuer votre raisonnement,parce que je ne sais pas vraiment comment résoudre l'inéquation résultant en rendant la substitution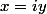 .Je crois que mon raisonnement pour résoudre ces types d'inéquations est plus court et plus sûr.Il est plus facile à pour résoudre l'équation
.Je crois que mon raisonnement pour résoudre ces types d'inéquations est plus court et plus sûr.Il est plus facile à pour résoudre l'équation
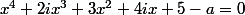 où [TEX]a24i+3 ou même si i>2i etc... c'est pourquoi on se ramène aux réels, sinon comme l'ont habilement proposé les autres tu peux poser une relation d'ordre complexe du style x>=y ssi Re(x)>=Re(y))
où [TEX]a24i+3 ou même si i>2i etc... c'est pourquoi on se ramène aux réels, sinon comme l'ont habilement proposé les autres tu peux poser une relation d'ordre complexe du style x>=y ssi Re(x)>=Re(y))
S'il vous plaît continuer votre raisonnement,parce que je ne sais pas vraiment comment résoudre l'inéquation résultant en rendant la substitution
Faire la substitution 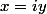 atteindre a l'inéquation
atteindre a l'inéquation 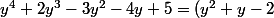^2+1<0) .Expliquez-moi s'il vous plaît ce résultat!L'inéquation
.Expliquez-moi s'il vous plaît ce résultat!L'inéquation 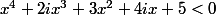 a des solutions?
a des solutions?
----------------------------------------------
Avec mon raisonnement sont calculées rapide les solutions de l'inéquation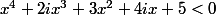 qui peut s'écrire
qui peut s'écrire 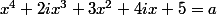 où
où 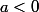 est un nombre réel et
est un nombre réel et 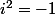 ,et puis, il s'ensuit
,et puis, il s'ensuit 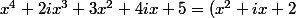^2+1=a) et evidemment les solutions de l'inéquation
et evidemment les solutions de l'inéquation 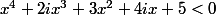 sont
sont 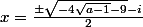 et
et 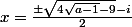 .Correctement ?Je dis,oui !
.Correctement ?Je dis,oui !
----------------------------------------------
Avec mon raisonnement sont calculées rapide les solutions de l'inéquation
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Dacu a écrit:Faire la substitutionatteindre a l'inéquation
.Expliquez-moi s'il vous plaît ce résultat!L'inéquation
a des solutions?
----------------------------------------------
Avec mon raisonnement sont calculées rapide les solutions de l'inéquationqui peut s'écrire
où
est un nombre réel et
,et puis, il s'ensuit
et evidemment les solutions de l'inéquation
sont
et
.Correctement ?Je dis,oui !
En gardant la forme en y en supposant y réel ton équation n'a pas de solutions. Donc les imaginaires purs ça ne marche pas. Ensuite ce ne sont peut être pas les seules solutions possibles. Pour trouver l'ensemble des solutions ayant un sens il faut que tu remplaces x par x=a+ib, et que tu annules la partie imaginaire (tu trouveras une relation entre a et b je suppose et pour vérifier la cohérence de ton résultat il faut que l'ensemble des imaginaires soit inclu dans les solutions) ensuite tu remplaces x par les valeurs possibles qu'il peut prendre et tu résoud ton équation. Toi, tu résouts ton équation sans passer par la première étape, je n'ai pas vérifié si ça fonctionnait mais il est possible que finalement tu compares des complexes à des réels.
Finalement j'imagine que tu cherches un intervalle de x si tu veux résoudre ton équation. Donc sachant a<0 pour trouver ton intervalle de x tu vas galérer donc c'est pas spécialement une bonne idée de poser a<0. Après j'aimerais bien que certains plus compétents que moi me disent ce qu'ils en pensent j'ai peur de dire des aneries mais à priori ça n'est pas la bonne méthode et ne pas passer par la première étape n'a pas de sens.
32 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
