Bonjour,
C'est une belle question.
Je pense que cette question peut s'inscrire dans une autre plus générale: à quoi servent les maths dans la vraie vie, et plus précisément, "à quoi peuvent servir des maths de lycée voire du supérieur dans la vie".
A cette question, on peut répondre de deux grandes manières: soit à s'obstiner à vouloir donner des exemples concrets, et ces exemples vont paraitre de plus en plus "forcés" au fur et à mesure que l'on avance dans la théorie: à quoi sert l'intégrale de Riemann dans la vie de tous les jours? à quoi servent les nombres complexes à part pour faire faire des calculs à rallonge dans la vie de tous les jours?
Et si on arrive assez rapidement à donner des "exemples partiels" (donc souvent flous car on ne rentre pas dans le détail) sur ces notions de lycée, on peut pousser un peu plus le questionnement: à quoi sert la théorie des anneaux ? à quoi servent les K-modules sur un anneau dans la vraie vie? A quoi servent les opérateurs compacts?
La deuxième manière de répondre à ces questions là, c'est celle que je donnerais moi: à rien.
Mis à part manger, dormir, et faire pipi, comme l'art ou la musique, ces notions ne servent à rien dans la vraie vie. D'ailleurs nombre de personnes vivent bien sans savoir ce qu'est une dérivée...
Comme le dit Ben, on peut vivre comme un "no brain" même si c'est un peu fort comme expression. C'est à dire vivre selon l'intuition/le feeling, retenir "comment" marchent les choses sans trop chercher le pourquoi de ce comment.
Ou bien on peut faire un choix délibéré de s'intéresser au monde qui nous entoure de manière plus ou moins mathématique et cartésienne et de se dire que même si une notion a priori théorique ne se rencontre pas "spontanément" en se brossant les dents, qu'elle peut toujours servir, soit ailleurs dans la théorie, soit comme tu le dis "dans la vraie vie" des sciences appliquées. Mais que au-delà de ça, l'utilité immédiate ne devrait pas être l'unique motivation d'appréhender une notion. Et si on accepte cette vision des choses, on se rend rapidement compte qu'il y a tout un monde "mystérieux" (les maths) dans lequel les notions interagissent entre elles librement...
Qui aurait cru qu'utiliser des nombres "imaginaires" pouvait permettre de trouver des résultats sur les réels? Qui aurait pu entrevoir un lien quelconque entre la somme infinie (1 + 1/2^2 + 1/3^2...) et le nombre pi !?
Et pourtant il se trouve que
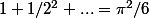
Mais ton questionnement est tout à fait légitime ! Et fort heureusement pour cette notion particulière, les applications observables sont très nombreuses, pour peu qu'on s'intéresse un peu au monde qui nous entoure.
Si tu lances un petit ballon (ou un projectile) avec une certaine vitesse, tu peux, selon ses caractéristiques, deviner quand est-ce qu'il atteindra le sol grace au concept de dérivation. Bien entendu, il faut d'abord savoir si pour toi cela fait partie de la "vie de tous les jours".
La dérivation intervient aussi dans les problèmes d'optimisation ! Si tu as une idée de l'évolution d'une quantité f en fonction du temps t, tu peux essayer de savoir pour quel t la valeur de f est la plus grande possible, ou la plus petite possible (recherche d'extremas locaux). Tu cherches t tel que f'(t) = 0 (en gros en quel t est-ce que f "ne varie plus", puisque dériver au voisinage de t, c'est regarder les variations de f au voisinage de t.
Cette méthode peut s'étendre à plusieurs variables.
Par exemple, quel est le point d'un dôme le plus haut possible? Tu répondras "bah son sommet". Mais si je te donne un autre type de configuration comme celle-ci:
http://www.mathworld.wolfram.com/images/eps-gif/WaveEquationRectangle_1000.gifla dérivation peut aussi permettre de trouver les points "sommets" et "creux" ! On définit alors la notion de dérivée partielle: f est une fonction de (x;y) car en chaque point (x;y) du plan on a une valeur f(x;y).
On peut alors définir f(x;y)/dx ou f(x;y)/dy et on cherche les points x et y tels que on ait à la fois f(x;y)/dx = 0 et f(x;y)/dy = 0
Donc si on s'intéresse à ce genre de choses, la dérivation est vraiment un outil puissant...pour peu qu'on s'y intéresse...! Si tu nous dis quels types de problèmes t'intéressent (exemple le problème du ballon, ou les problèmes d'optimisation...) ce sera avec plaisir qu'on développera tel ou tel exemple (et qu'on déroulera les calculs pour te convaincre)
PS: Les conditions du style f'(t) = 0 sont nécessaires non suffisantes.


