Formule pour générer les nombres premiers successifs et les
20 messages
- Page 1 sur 1
Formule pour générer les nombres premiers successifs et les
Bonjour,
Jai trouvé, dans la formule de pi en fonction du nombre dor, une curiosité (clic sur « more digits »)
Pi = ((4 Sum[((-1)^k/(2 k + 1))((goldenratio^(-2k-1))+goldenratio^(-6k-3)), {k, 0, infinity}]))
http://2doc.net/6nund
Exemple avec k = 37 http://2doc.net/y78lf
Son diviseur : http://www.wolframalpha.com/input/?i=256596987775268852148914337861
Le dernier chiffre des séquences est proche de 2k
Pour k = 37, 36
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53×59×61×67×71×73
Pour k = 35
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53×59×61×67x71
Pour k = 34, 33
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53×59×61×67
Pour k = 32, 31, 30
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53×59×61
Pour k = 29
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53×59
Pour k = 28, 27, 26
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53
Pour k = 25, 24
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47
Pour k = 23 (perd un 7)
3^3×7×11×13×17×19×23×29×31×37×41×43×47
Pour k = 22, 21
3^3×7×11×13×17×19×23×29×31×37×41×43
Pour k = 20
3^3×7×11×13×17×19×23×29×31×37×41
Pour k = 19,18
3^3×7×11×13×17×19×23×29×31×37
Pour k = 17,16, 15
3^3×7×11×13×17×19×23×29×31
Pour k = 14
3^3×7×11×13×17×19×23×29
Pour k =13
3^3×7×11×13×17×19×23
Pour k = 12 (perd un 3), 11
3^2×7×11×13×17×19×23
Pour k = 10, 9
3^2×7×11×13×17×19
Pour k = 8
3^2×7×11×13×17
Pour k = 7,6
3^2×7×11×13
Pour k = 5
3^2×7×11
Pour k = 4
3^2×7
Pour k = 3 (perd un 3)
3x7
Pour k = 2, 1
3
Plus de nombres en modifiant la formule
http://2doc.net/i4h3h
ou
http://2doc.net/qc9ao
Alors avec le diviseur, on a
http://www.wolframalpha.com/input/?i=260255629832446451879396196008752817240807621800046254926375
Pour trouver (ou vérifier un nombre premier), on donne à k une valeur quelconque (ou approximativement P/2) et on trouve un nombre premier approximatif à 2k
Exemple avec k=1859, 1860
http://2doc.net/5uy2d
on a alors 3719
http://www.wolframalpha.com/input/?i=13838399
Exemple avec k=6745, 6743
http://2doc.net/8pt6m
on a alors 13487
http://www.wolframalpha.com/input/?i=181872195
Je n'ai fait qu'une courte vérification sans avoir trouvé encore de contre-exemple.
Jai trouvé, dans la formule de pi en fonction du nombre dor, une curiosité (clic sur « more digits »)
Pi = ((4 Sum[((-1)^k/(2 k + 1))((goldenratio^(-2k-1))+goldenratio^(-6k-3)), {k, 0, infinity}]))
http://2doc.net/6nund
Exemple avec k = 37 http://2doc.net/y78lf
Son diviseur : http://www.wolframalpha.com/input/?i=256596987775268852148914337861
Le dernier chiffre des séquences est proche de 2k
Pour k = 37, 36
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53×59×61×67×71×73
Pour k = 35
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53×59×61×67x71
Pour k = 34, 33
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53×59×61×67
Pour k = 32, 31, 30
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53×59×61
Pour k = 29
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53×59
Pour k = 28, 27, 26
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53
Pour k = 25, 24
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47
Pour k = 23 (perd un 7)
3^3×7×11×13×17×19×23×29×31×37×41×43×47
Pour k = 22, 21
3^3×7×11×13×17×19×23×29×31×37×41×43
Pour k = 20
3^3×7×11×13×17×19×23×29×31×37×41
Pour k = 19,18
3^3×7×11×13×17×19×23×29×31×37
Pour k = 17,16, 15
3^3×7×11×13×17×19×23×29×31
Pour k = 14
3^3×7×11×13×17×19×23×29
Pour k =13
3^3×7×11×13×17×19×23
Pour k = 12 (perd un 3), 11
3^2×7×11×13×17×19×23
Pour k = 10, 9
3^2×7×11×13×17×19
Pour k = 8
3^2×7×11×13×17
Pour k = 7,6
3^2×7×11×13
Pour k = 5
3^2×7×11
Pour k = 4
3^2×7
Pour k = 3 (perd un 3)
3x7
Pour k = 2, 1
3
Plus de nombres en modifiant la formule
http://2doc.net/i4h3h
ou
http://2doc.net/qc9ao
Alors avec le diviseur, on a
http://www.wolframalpha.com/input/?i=260255629832446451879396196008752817240807621800046254926375
Pour trouver (ou vérifier un nombre premier), on donne à k une valeur quelconque (ou approximativement P/2) et on trouve un nombre premier approximatif à 2k
Exemple avec k=1859, 1860
http://2doc.net/5uy2d
on a alors 3719
http://www.wolframalpha.com/input/?i=13838399
Exemple avec k=6745, 6743
http://2doc.net/8pt6m
on a alors 13487
http://www.wolframalpha.com/input/?i=181872195
Je n'ai fait qu'une courte vérification sans avoir trouvé encore de contre-exemple.
Salut,
Juste une remarque : ta formule "de base" contient, entre autre, une division par 2k+1.
Donc le fait qu'en prenant k=1859 (plus d'autres valeurs) tu obtienne 3719=2x1859+1 comme facteur dans le dénominateur ne me semble pas très étonnant.
Et je dirais même plus, lorsque tu prend k=1859, 1860 le fait que le dénominateur soit 13838399=61²x3719 avec 3719=2x1859+1 et 61²=3721=2x1860+1 me semble quand même assez normal.
Aprés, concernant^k}{2k+1}\big(\varphi^{-2k-1}+\varphi^{-6k-3}\big)) , vu que
, vu que 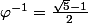 , un multiple commun des dénominateur va être une puissance de deux fois le produit des nombres premiers p<=2n+1 à une puissance k telle que p^k<=2n+1.
, un multiple commun des dénominateur va être une puissance de deux fois le produit des nombres premiers p<=2n+1 à une puissance k telle que p^k<=2n+1.
Par exemple, si tu veut réduire au même dénominateur des fractions dont les dénominateurs sont respectivement 1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31, tu prend le ppcm de tout ça et c'est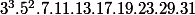
Donc le seul truc un peu "miraculeux" qu'il y ait, c'est que la seule simplification qu'il semble y avoir avec le numérateur, c'est uniquement les puissances de deux et de 5 qui se simplifient (ça doit sans doute pouvoir se démontrer en particulier pour le 5 vu le racine(5) qui apparait dans le nombre d'or)
Tout ça pour dire que, si à la place du nombre d'or dans tes formules, tu prenait bêtement 1/1+1/3+1/5+1/7+...+1/(2n+1) ou bien 1/1-1/3+1/5-1/7...+(-1)^n/(2n+1) alors il y a de forte chances que tu obtienne à peu prés les même propriétés pour le dénominateur :
[url]http://www.wolframalpha.com/input/?i=Sum[1%2F%282+k+%2B+1%29%29%2C+{k%2C+0%2C+37}][/url]
http://www.wolframalpha.com/input/?i=6414924694381721303722858446525
Juste une remarque : ta formule "de base" contient, entre autre, une division par 2k+1.
Donc le fait qu'en prenant k=1859 (plus d'autres valeurs) tu obtienne 3719=2x1859+1 comme facteur dans le dénominateur ne me semble pas très étonnant.
Et je dirais même plus, lorsque tu prend k=1859, 1860 le fait que le dénominateur soit 13838399=61²x3719 avec 3719=2x1859+1 et 61²=3721=2x1860+1 me semble quand même assez normal.
Aprés, concernant
Par exemple, si tu veut réduire au même dénominateur des fractions dont les dénominateurs sont respectivement 1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31, tu prend le ppcm de tout ça et c'est
Donc le seul truc un peu "miraculeux" qu'il y ait, c'est que la seule simplification qu'il semble y avoir avec le numérateur, c'est uniquement les puissances de deux et de 5 qui se simplifient (ça doit sans doute pouvoir se démontrer en particulier pour le 5 vu le racine(5) qui apparait dans le nombre d'or)
Tout ça pour dire que, si à la place du nombre d'or dans tes formules, tu prenait bêtement 1/1+1/3+1/5+1/7+...+1/(2n+1) ou bien 1/1-1/3+1/5-1/7...+(-1)^n/(2n+1) alors il y a de forte chances que tu obtienne à peu prés les même propriétés pour le dénominateur :
[url]http://www.wolframalpha.com/input/?i=Sum[1%2F%282+k+%2B+1%29%29%2C+{k%2C+0%2C+37}][/url]
http://www.wolframalpha.com/input/?i=6414924694381721303722858446525
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Merci Ben pour cette analyse.
J'avais aussi regardé cette simplification, maiis il manque des chiffres :
http://www.wolframalpha.com/input/?i=Sum%5B1%2F%282+k+%2B+1%29%29%2C+%7Bk%2C+0%2C+70%7D%5D
le nombre 23 au moins
http://www.wolframalpha.com/input/?i=11315462166628106603452008522119687706122070513045489344625
Avec la formule de Biwabik, modifiée pour plus de résultats :
http://www.wolframalpha.com/input/?i=%284+Sum%5B%28%28-1%29%5Ek%2F%282+k+%2B+1%29%29%28%28goldenratio%5E%28-2k-1%29%29*goldenratio%5E%28-6k-3%29%29%2C+%7Bk%2C+0%2C+70%7D%5D%29
A moins d'un trou noir dans mon cerveau, ça me semble correct
http://www.wolframalpha.com/input/?i=260255629832446451879396196008752817240807621800046254926375
Il faudrait que je prenne le temps de vérifier avec de grands chiffres, mais wolfram a ses limites (merci wolfram quand même !).
J'avais aussi regardé cette simplification, maiis il manque des chiffres :
http://www.wolframalpha.com/input/?i=Sum%5B1%2F%282+k+%2B+1%29%29%2C+%7Bk%2C+0%2C+70%7D%5D
le nombre 23 au moins
http://www.wolframalpha.com/input/?i=11315462166628106603452008522119687706122070513045489344625
Avec la formule de Biwabik, modifiée pour plus de résultats :
http://www.wolframalpha.com/input/?i=%284+Sum%5B%28%28-1%29%5Ek%2F%282+k+%2B+1%29%29%28%28goldenratio%5E%28-2k-1%29%29*goldenratio%5E%28-6k-3%29%29%2C+%7Bk%2C+0%2C+70%7D%5D%29
A moins d'un trou noir dans mon cerveau, ça me semble correct
http://www.wolframalpha.com/input/?i=260255629832446451879396196008752817240807621800046254926375
Il faudrait que je prenne le temps de vérifier avec de grands chiffres, mais wolfram a ses limites (merci wolfram quand même !).
Il semblerais effectivement qu'il n'y ait jamais d'autres simplifications que la puissance de 2.
Mais d'un autre coté, contrairement à la "bête" somme des 1/(2k+1), pour que ça se simplifie, il faut un diviseur commun au dénominateur et aux deux entiers apparaissant au numérateur : ça semble donc moins probable que pour la somme des 1/(2k+1).
Mais bon, de toute façon, ton dénominateur, c'est à peu de chose prés le ppcm des 2k+1 pour k entre 1 et n et il n'y a clairement rien d'étonnant à ce que, la décomposition en nombre premier du produit des impairs <=2n+1 contienne tout les nombres premiers inférieur à 2n+1...
Donc si ton but est de faire apparaitre des décompositions de la forme :
Pour k = 37, 36
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53×59×61× 67×71×73
Prend directement le pgcd des 2k+1 pour k de 0 à n : ça ira plus vite.
Mais d'un autre coté, contrairement à la "bête" somme des 1/(2k+1), pour que ça se simplifie, il faut un diviseur commun au dénominateur et aux deux entiers apparaissant au numérateur : ça semble donc moins probable que pour la somme des 1/(2k+1).
Mais bon, de toute façon, ton dénominateur, c'est à peu de chose prés le ppcm des 2k+1 pour k entre 1 et n et il n'y a clairement rien d'étonnant à ce que, la décomposition en nombre premier du produit des impairs <=2n+1 contienne tout les nombres premiers inférieur à 2n+1...
Donc si ton but est de faire apparaitre des décompositions de la forme :
Pour k = 37, 36
3^3×7^2×11×13×17×19×23×29×31×37×41×43×47×53×59×61× 67×71×73
Prend directement le pgcd des 2k+1 pour k de 0 à n : ça ira plus vite.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ce qui me semble très intéressant si la formule s'avérait donner la séquence des nombres premier ou en vérifier un élément (très loin d'être banal), c'est le lien étroit possible entre pi, phi et les nombres premiers.
On est quand même, avec ces quantités, à la source de la mathématique, à sa cause et celle de l'univers.
Démo formule
http://fred.elie.free.fr/nombre_d_or_et_fibonacci.pdf (page 27 à 30)
On est quand même, avec ces quantités, à la source de la mathématique, à sa cause et celle de l'univers.
Démo formule
http://fred.elie.free.fr/nombre_d_or_et_fibonacci.pdf (page 27 à 30)
Sauf que là où apparaissent tes nombres premier, c'est dans le ppcm(1,3,5,7,...,2n+1) :
1) C'est évidement totalement "banal" (pour ne pas dire "trivial") que les nombres premiers impairs <=2n+1 apparaissent dans le ppcm(1,3,5,7,...,2n+1).
2) ce ppcm n'a rien à voir ni avec pi ni avec le nombre d'or vu qu'il ne dépend que des dénominateurs des fractions que tu ajoute alors que le nombre d'or est au numérateur et que, vu que tes somme ne sont pas égales à pi mais approximent pi, les dénominateurs de tes fractions n'ont absolument aucun lien avec pi : de savoir que la fraction a/b approxime pi ne donne évidement pas le début de la moitié d'une information sur b !!!
Pour te donne un exemple totalement débile, il est clair que si tu veut écrire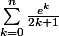 sous la forme d'une fraction avec au numérateur un polynôme à coeff. entier en
sous la forme d'une fraction avec au numérateur un polynôme à coeff. entier en  , le dénominateur sera clairement le ppcm(1,3,...,2n+1) vu qu'il n'y a aucune simplification possible.
, le dénominateur sera clairement le ppcm(1,3,...,2n+1) vu qu'il n'y a aucune simplification possible.
Et dans la somme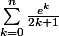 , si tu remplace
, si tu remplace  par tout autre nombre transcendant (par exemple pi), ça donnera exactement le même résultat.
par tout autre nombre transcendant (par exemple pi), ça donnera exactement le même résultat.
Après, si tu remplace le par un nombre algébrique, par exemple le nombre d'or ou
par un nombre algébrique, par exemple le nombre d'or ou 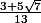 , il peut éventuellement y avoir des simplifications pour certains n, mais je pense que ça doit être plutôt rare et que le cas de loin le plus fréquent est celui de ta somme où le dénominateur de ton truc est le ppcm(1,3,...,2n+1).
, il peut éventuellement y avoir des simplifications pour certains n, mais je pense que ça doit être plutôt rare et que le cas de loin le plus fréquent est celui de ta somme où le dénominateur de ton truc est le ppcm(1,3,...,2n+1).
P.S. : Pour bien te convaincre, fait quelques essais en remplaçant dans tes calculs le nombre d'Or par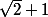 pour voir quelle tête ont les dénominateurs.
pour voir quelle tête ont les dénominateurs.
Bien évidement, les nouvelles sommes obtenues n'ont plus rien à voir avec pi, ni avec le nombre d'Or et pourtant...
1) C'est évidement totalement "banal" (pour ne pas dire "trivial") que les nombres premiers impairs <=2n+1 apparaissent dans le ppcm(1,3,5,7,...,2n+1).
2) ce ppcm n'a rien à voir ni avec pi ni avec le nombre d'or vu qu'il ne dépend que des dénominateurs des fractions que tu ajoute alors que le nombre d'or est au numérateur et que, vu que tes somme ne sont pas égales à pi mais approximent pi, les dénominateurs de tes fractions n'ont absolument aucun lien avec pi : de savoir que la fraction a/b approxime pi ne donne évidement pas le début de la moitié d'une information sur b !!!
Pour te donne un exemple totalement débile, il est clair que si tu veut écrire
Et dans la somme
Après, si tu remplace le
P.S. : Pour bien te convaincre, fait quelques essais en remplaçant dans tes calculs le nombre d'Or par
Bien évidement, les nouvelles sommes obtenues n'ont plus rien à voir avec pi, ni avec le nombre d'Or et pourtant...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Je ne comprends pas.
Au dénominateur il y a aussi phi dans la formule originale
http://www.wolframalpha.com/input/?i=%284+Sum%5B%28%28-1%29%5Ek%2F%282+k+%2B+1%29%29%28%28goldenratio%5E%28-2k-1%29%29%2Bgoldenratio%5E%28-6k-3%29%29%2C+%7Bk%2C+0%2C+37%7D%5D%29
ou dans les formules modifiées comme
http://www.wolframalpha.com/input/?i=%284+Sum%5B%28%28-1%29%5Ek%2F%282+k+%2B+1%29%29%28%28goldenratio%5E%28-2k-1%29%29*goldenratio%5E%28-6k-3%29%29%2C+%7Bk%2C+0%2C+70%7D%5D%29
Comment expliques-tu dans ton premier exemple que la séquence des nombres premiers soit incomplète ?
Peux-tu donner un exemple selon ce que tu dis qui donne une séquence complète,donc sans omission de premiers ?
Au dénominateur il y a aussi phi dans la formule originale
http://www.wolframalpha.com/input/?i=%284+Sum%5B%28%28-1%29%5Ek%2F%282+k+%2B+1%29%29%28%28goldenratio%5E%28-2k-1%29%29%2Bgoldenratio%5E%28-6k-3%29%29%2C+%7Bk%2C+0%2C+37%7D%5D%29
ou dans les formules modifiées comme
http://www.wolframalpha.com/input/?i=%284+Sum%5B%28%28-1%29%5Ek%2F%282+k+%2B+1%29%29%28%28goldenratio%5E%28-2k-1%29%29*goldenratio%5E%28-6k-3%29%29%2C+%7Bk%2C+0%2C+70%7D%5D%29
Comment expliques-tu dans ton premier exemple que la séquence des nombres premiers soit incomplète ?
Peux-tu donner un exemple selon ce que tu dis qui donne une séquence complète,donc sans omission de premiers ?
Un petit "rappel" :fma a écrit:Au dénominateur il y a aussi phi dans la formule originale
Donc
Jusque là, tout ça n'a rien à voir avec pi, ni avec le nombre d'or. Tu aurais mis
J'explique ça par... un truc qu'on voit (plus ou moins) au collège, à savoir que, pour ajouter des fraction on commence par les "réduire au même dénominateur" et que ce dénominateur commun est le ppcm des dénominateurs.fma a écrit:Comment expliques-tu dans ton premier exemple que la séquence des nombres premiers soit incomplète ?
Lorsque l'on prend des fractions un peu grande et totalement au pif, la plupart du temps, il n'y aura pas de simplification et donc le dénominateur du résultat sera effectivement le ppcm des dénominateurs.
MAIS il peut arriver qu'il y ait simplification, par exemple 1/2+1/6=3/6+1/6=4/6=2/3 dont le dénominateur aprés simplification est 3 alors que le ppcm(2,6)=6.
Donc dans l'exemple que je t'ai donné, j'ai pris les numérateurs les plus c.. qui soient, à savoir 1 tout le temps et, effectivement, il s'avère qu'il y a une simplification dans la fraction obtenue (je sais pas si c'est facile à prévoir vu que, pour le coup, ça dépend à la fois des dénominateurs ET des numérateurs).
J'espère que tu est bien conscient que, plus les numérateurs que l'on met au dessus des 2k+1 du dénominateur sont complexes, moins il y a de chances que ça se simplifie et donc... plus il y de chances que le dénominateur du résultat soit le ppcm des dénominateurs.
Par exemple, dans la somme
Dans ton cas à toi, le numérateur est plus complexe et, après mise au même dénominateur, tes somme sont de la forme
Je te le redit, fait 3 essais avec par exemple
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Tu as dit que c'était "banal" et "trivial".
Donne donc une formule comme celle de Biwabik (modifiée dans le lien qui suit pour aller au delà de k=37, limite wolfram) qui semble engendrer une séquence de nombres premiers (sauf 2) successifs, sans aucune omission.
k<71
Exemple
Pour k=70
http://www.wolframalpha.com/input/?i=%284+Sum%5B%28%28-1%29%5Ek%2F%282+k+%2B+1%29%29%28%28goldenratio%5E%28-2k-1%29%29*goldenratio%5E%28-6k-3%29%29%2C+%7Bk%2C+0%2C+70%7D%5D%29
dénominateur
http://www.wolframalpha.com/input/?i=260255629832446451879396196008752817240807621800046254926375
******
Erreur sur ce que j'ai écrit plus bas
"Pour trouver (ou vérifier un nombre premier), on donne à k une valeur quelconque (ou approximativement P/2) et on trouve un nombre premier approximatif à 2k"
Exemple avec k=1859, 1860
http://2doc.net/5uy2d
on a alors 3719
http://www.wolframalpha.com/input/?i=13838399
Exemple avec k=6745, 6743
http://2doc.net/8pt6m
on a alors 13487
http://www.wolframalpha.com/input/?i=181872195
sauf que pour k=72,73
http://www.wolframalpha.com/input/?i=%284+Sum%5B%28%28-1%29%5Ek%2F%282+k+%2B+1%29%29%28%28goldenratio%5E%28-2k-1%29%29%2Bgoldenratio%5E%28-6k-3%29%29%2C+%7Bk%2C+72%2C+73%7D%5D%29
on a 3×7^2×29
http://www.wolframalpha.com/input/?i=4263
et 2x 29 est très différent de 72 ou 73
Donne donc une formule comme celle de Biwabik (modifiée dans le lien qui suit pour aller au delà de k=37, limite wolfram) qui semble engendrer une séquence de nombres premiers (sauf 2) successifs, sans aucune omission.
k<71
Exemple
Pour k=70
http://www.wolframalpha.com/input/?i=%284+Sum%5B%28%28-1%29%5Ek%2F%282+k+%2B+1%29%29%28%28goldenratio%5E%28-2k-1%29%29*goldenratio%5E%28-6k-3%29%29%2C+%7Bk%2C+0%2C+70%7D%5D%29
dénominateur
http://www.wolframalpha.com/input/?i=260255629832446451879396196008752817240807621800046254926375
******
Erreur sur ce que j'ai écrit plus bas
"Pour trouver (ou vérifier un nombre premier), on donne à k une valeur quelconque (ou approximativement P/2) et on trouve un nombre premier approximatif à 2k"
Exemple avec k=1859, 1860
http://2doc.net/5uy2d
on a alors 3719
http://www.wolframalpha.com/input/?i=13838399
Exemple avec k=6745, 6743
http://2doc.net/8pt6m
on a alors 13487
http://www.wolframalpha.com/input/?i=181872195
sauf que pour k=72,73
http://www.wolframalpha.com/input/?i=%284+Sum%5B%28%28-1%29%5Ek%2F%282+k+%2B+1%29%29%28%28goldenratio%5E%28-2k-1%29%29%2Bgoldenratio%5E%28-6k-3%29%29%2C+%7Bk%2C+72%2C+73%7D%5D%29
on a 3×7^2×29
http://www.wolframalpha.com/input/?i=4263
et 2x 29 est très différent de 72 ou 73
Bon, je te l'ai déjà dit dix fois (et ce sera la dernière) : il n'y a pas le moindre miracle : tu ajoute des fractions dont les dénominateurs sont 3,5,7,9,...,2n+1 et, une fois que tu as tout mis au même dénominateur et ajouté, ton dénominateur c'est le ppcm(3,5,7,...,2n+1) ce qui est on ne peut plus "banal" : ce qui serait exceptionnel, c'est exactement le contraire, à savoir qu'il y ait des tas de simplifications et qu'il reste un dénominateur bien plus petit que le ppcm des dénominateurs.
Prend au pif une dizaine de fractions un peu grandes, demande à Wolfram de les ajouter et regarde si "l'exceptionnel" c'est que le dénominateur du résultat soit le ppcm ou pas : ça devrait te convaincre que ton truc, c'est tout ce qu'il y a de plus "la normalité".
Aprés, concernant le "un autre exemple", ç'est... la troisième fois que je te le donne (et de nouveau la dernière) : prend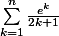 dont le seul point commun avec tes sommes, c'est le 2k+1 au dénominateur. (je suis tranquille, vu que
dont le seul point commun avec tes sommes, c'est le 2k+1 au dénominateur. (je suis tranquille, vu que  est transcendant, ça risque pas de se simplifier...)
est transcendant, ça risque pas de se simplifier...)
[url]http://www.wolframalpha.com/input/?i=Sum[e^k%2F+%282+k+%2B+1%29%2C+{k%2C+0%2C+70}][/url]
dénominateur :
http://www.wolframalpha.com/input/?i=260255629832446451879396196008752817240807621800046254926375
MIRACLE : CA FAIT LE PRODUIT DES NOMBRES PREMIERS !!!!
Et si ça t'amuse je le redit (de nouveau pour la 3em fois...), met pi à la place de e, voir même encore plus bêtement tu met X et... encore un miracle...
Pour finir (je ne répondrais plus), si tu veut absolument que ce soit "un miracle", et ben y'a qu'a dire que c'est "un miracle", mais il faudrait quand même que tu comprenne que ton "miracle", c'est la constatation que, quand on ajoute des tiers avec des cinquièmes, ben la plupart du temps, le résultat, c'est des quinzièmes.
Prend au pif une dizaine de fractions un peu grandes, demande à Wolfram de les ajouter et regarde si "l'exceptionnel" c'est que le dénominateur du résultat soit le ppcm ou pas : ça devrait te convaincre que ton truc, c'est tout ce qu'il y a de plus "la normalité".
Aprés, concernant le "un autre exemple", ç'est... la troisième fois que je te le donne (et de nouveau la dernière) : prend
[url]http://www.wolframalpha.com/input/?i=Sum[e^k%2F+%282+k+%2B+1%29%2C+{k%2C+0%2C+70}][/url]
dénominateur :
http://www.wolframalpha.com/input/?i=260255629832446451879396196008752817240807621800046254926375
MIRACLE : CA FAIT LE PRODUIT DES NOMBRES PREMIERS !!!!
Et si ça t'amuse je le redit (de nouveau pour la 3em fois...), met pi à la place de e, voir même encore plus bêtement tu met X et... encore un miracle...
Pour finir (je ne répondrais plus), si tu veut absolument que ce soit "un miracle", et ben y'a qu'a dire que c'est "un miracle", mais il faudrait quand même que tu comprenne que ton "miracle", c'est la constatation que, quand on ajoute des tiers avec des cinquièmes, ben la plupart du temps, le résultat, c'est des quinzièmes.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Donc, si je comprend bien, pour trouver un nombre premier environ égal à 2k, tu calcule (ou plutôt tu fait calculer à wolfram) le ppcm(3,5,7,9,...,2k+1) puis tu lui demande de factoriser ce ppcm et ça te permet de trouver le plus grand nombre premier inférieur à 2k+1.... :mur:fma a écrit:Pour trouver (ou vérifier un nombre premier), on donne à k une valeur quelconque (ou approximativement P/2) et on trouve un nombre premier approximatif à 2k
Tu as pas un tout petit peu l'impression que ça tourne complètement en rond ton truc ?
A ton avis, pour factoriser ton fameux ppcm, il fait comment Wolfram ?
Sinon, je te propose une autre formule qui a le bon gout d'être encore plus courte : pour obtenir un truc dont la décomposition en facteur premier contient tout les entiers inférieurs à un entier donné N, tu demande directement à Wolfram de te factoriser factorielle de N : c'est moins long à taper que ta formule... :zen:
72! -> http://www.wolframalpha.com/input/?i=72!
On réinjecte le résultat -> http://www.wolframalpha.com/input/?i=61234458376886086861524070385274672740778091784697328983823014963978384987221689274204160000000000000000
MIRACLE !!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui, mais 3x7²x29 n'est pas trés différent de (2x72+1)x(2x73+1) et, à la différence de tes exemples précédent, ni 2x72+1, ni 2x73+1 ne sont premier.fma a écrit:sauf que pour k=72,73
http://www.wolframalpha.com/input/?i=%284+Sum%5B%28%28-1%29%5Ek%2F%282+k+%2B+1%29%29%28%28goldenratio%5E%28-2k-1%29%29%2Bgoldenratio%5E%28-6k-3%29%29%2C+%7Bk%2C+72%2C+73%7D%5D%29
on a 3×7^2×29
http://www.wolframalpha.com/input/?i=4263
et 2x 29 est très différent de 72 ou 73
Donc ta méthode, elle permet de trouver un 2k+1 qui est premier à l'unique condition de... partir d'un k tel que 2k+1 est premier... : génial !!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonjour,
Préambule rectificatif :
Je commence à comprendre ce que tu expliques, alors je te présente mes excuses pour mon esprit un peu bouché.
J'y réfléchis, mais peux-tu quand même répondre à la question posée pour une formule simple qui passe au crible un dénominateur en fait relativement léger en puissance de premiers. Merci
Il me semble, Ben314, que nous n'avons pas la même logique mathématique.
Tu contestes d'emblée un résultat que tu trouves trivial.
Alors je te demande de valider tes dires en donnant une formule sans doute triviale donc.
Au final, après multiples circonvolutions, tu cries au loup en accusant l'autre de tourner en rond, prenant la peine au passage de crucifier un hypothétique faiseur de miracles.
Soyons constructifs :
Ce qui serait intéressant, ce serait de comprendre le rôle de pi et phi dans le dénominateur, mais cest vrai que pour toi il nont rien à voir là-dedans.
Donne donc , sans pi et sans phi, une formule comme celle de Biwabik (modifiée dans le lien qui suit pour aller au-delà de k=37, limite wolfram) qui semble engendrer une séquence de nombres premiers (sauf 2) successifs, sans aucune omission,
et tout rentrera dans l'ordre. Tu as à ta disposition tous les outils du web.
Pour k=70
http://www.wolframalpha.com/input/?i=%284+Sum%5B%28%28-1%29%5Ek%2F%282+k+%2B+1%29%29%28%28goldenratio%5E%28-2k-1%29%29*goldenratio%5E%28-6k-3%29%29%2C+%7Bk%2C+0%2C+70%7D%5D%29
dénominateur
http://www.wolframalpha.com/input/?i=260255629832446451879396196008752817240807621800046254926375
P.S.
J'avais bien écrit "Erreur" sur ce paragraphe, constatant l'invalidité ou le doute dans mes vérifications
Préambule rectificatif :
Je commence à comprendre ce que tu expliques, alors je te présente mes excuses pour mon esprit un peu bouché.
J'y réfléchis, mais peux-tu quand même répondre à la question posée pour une formule simple qui passe au crible un dénominateur en fait relativement léger en puissance de premiers. Merci
Il me semble, Ben314, que nous n'avons pas la même logique mathématique.
Tu contestes d'emblée un résultat que tu trouves trivial.
Alors je te demande de valider tes dires en donnant une formule sans doute triviale donc.
Au final, après multiples circonvolutions, tu cries au loup en accusant l'autre de tourner en rond, prenant la peine au passage de crucifier un hypothétique faiseur de miracles.
Soyons constructifs :
Ce qui serait intéressant, ce serait de comprendre le rôle de pi et phi dans le dénominateur, mais cest vrai que pour toi il nont rien à voir là-dedans.
Donne donc , sans pi et sans phi, une formule comme celle de Biwabik (modifiée dans le lien qui suit pour aller au-delà de k=37, limite wolfram) qui semble engendrer une séquence de nombres premiers (sauf 2) successifs, sans aucune omission,
et tout rentrera dans l'ordre. Tu as à ta disposition tous les outils du web.
Pour k=70
http://www.wolframalpha.com/input/?i=%284+Sum%5B%28%28-1%29%5Ek%2F%282+k+%2B+1%29%29%28%28goldenratio%5E%28-2k-1%29%29*goldenratio%5E%28-6k-3%29%29%2C+%7Bk%2C+0%2C+70%7D%5D%29
dénominateur
http://www.wolframalpha.com/input/?i=260255629832446451879396196008752817240807621800046254926375
P.S.
Ben314 a écrit:Oui, mais 3x7²x29 n'est pas trés différent de (2x72+1)x(2x73+1) et, à la différence de tes exemples précédent, ni 2x72+1, ni 2x73+1 ne sont premier.
Donc ta méthode, elle permet de trouver un 2k+1 qui est premier à l'unique condition de... partir d'un k tel que 2k+1 est premier... : génial !!!
J'avais bien écrit "Erreur" sur ce paragraphe, constatant l'invalidité ou le doute dans mes vérifications
J'ai déjà répondu (au moins 3 fois) à chacune des questions du post çi dessus (en particulier celle demandant d'autres formules sans pi ni phi dont la décomposition en nombres premiers contient tout les nombres premiers <=N. La dernière donnée et de loin la plus simple, c'est factorielle(N)... )
Donc... LIT les réponses qu'on te fait.... et on en reparlera ensuite.
Donc... LIT les réponses qu'on te fait.... et on en reparlera ensuite.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
fma a écrit:Bon je comprends que tu ne peux pas donner de formules triviales donnant donc un tel tri.
Tant pis.
A+
non (enfin... à part juste trois fois...)
ça, c'est sûr que la formule
" le dénominateur de la somme de k=0 à n de (-1)^k(phi^{-2k-1}+phi^{-6k+3}) une fois les fraction ajoutées et les simplification effectuées"
est trés beaucoup plus "triviale" que la formule
"factorielle(N)"
LIT LES REPONSES QU'ON TE FAIT
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ton post
[url=http://www.wolframalpha.com/input/?i=Sum[e^k%2F+%282+k+%2B+1%29%2C+{k%2C+0%2C+70}]Ta formule[/url]
dénominateur :
http://www.wolframalpha.com/input/?i=260255629832446451879396196008752817240807621800046254926375
Bien joué, je suis mat.
J'ai mangé tout le chocolat
[url=http://www.wolframalpha.com/input/?i=Sum[e^k%2F+%282+k+%2B+1%29%2C+{k%2C+0%2C+70}]Ta formule[/url]
dénominateur :
http://www.wolframalpha.com/input/?i=260255629832446451879396196008752817240807621800046254926375
Bien joué, je suis mat.
J'ai mangé tout le chocolat
Et c'est d'autant plus vrai que dans
http://www.hostingpics.net/viewer.php?id=934213Capture.gif
ou
http://urlz.fr/tNs
on a pas besoin de phi pour exprimer pi
http://urlz.fr/tNw
J'ai mangé une deuxième plaquette de chocolat ; il paraît c'est bon pour le moral.
http://www.hostingpics.net/viewer.php?id=934213Capture.gif
ou
http://urlz.fr/tNs
on a pas besoin de phi pour exprimer pi
http://urlz.fr/tNw
J'ai mangé une deuxième plaquette de chocolat ; il paraît c'est bon pour le moral.
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
