Réflexions sur les nombres premiers

[Thierry39]

Bonjour,
je ne suis pas mathématicien mais j'ai toujours aimé les mathématiques à mon niveau (Niveau Lycée), merci d'être tolérant avec ma manière de rédiger ! J'ai écris la réflexion ci-dessous où j'essaie de voir s'il est possible ou non de trouver une formule qui donnerait la valeur d'un nombre premier à une position arbitraire de la séquence des nombres premiers.
Merci d'avance à ceux qui feront l'effort de me lire et de me dire si mon raisonnement est correct ou non. Si la démonstration logique que j'essaie de réaliser est suffisante ou non.

Voici mon analyse :

1 Définition
Un nombre premier se définit comme suit :
Un nombre est appelé « Nombre premier » s’il n’est divisible que par 1 et par lui-même. Par convention le nombre 1 n’est pas considéré comme un nombre premier.

Exemple : 7 est un nombre premier car il n’est pas divisible par 2, ni par 3, ni par 5.
Liste des nombres premiers inférieurs à 100 :
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

2 La fonction des nombres premiers
Depuis toujours les mathématiciens ont cherché en vain une fonction qui permettrait de donner directement le nième nombre premier. Appelons « f » cette hypothétique fonction, définit comme suit :

Avec « n » le numéro de séquence du nombre premier dans la liste des nombres premiers et « Pn » la valeur du nième nombre premier.
Exemples : f(1) = 2, f(2) = 3, f(3) = 5, … f(25) = 97 etc..
Les analyses statistiques réalisées sur les premiers milliards des nombres premiers laissent à penser que les nombres premiers apparaissent de manière quasi aléatoire, aucune séquence logique ne semble visible dans cette liste. Ce fait semble conforté par l’apparition permanente de nombres premiers jumeaux de grande valeur numérique.
Deux nombres premiers sont dit « jumeaux » lorsque que leur différence fait 2.
Exemple 29 et 31 sont deux nombres premiers jumeaux.
Il a été prouvé que le nombre de premiers jumeaux est infini.

3 Conjecture
En désaccord avec l’analyse précédente je poserai la conjecture suivante :
La séquence de construction des nombres premiers est périodique. Elle est périodique par définition.

Dans ce cas, pour quelle raison aucune analyse, malgré la puissance de calcul des ordinateurs actuels, n’a pu montrer une telle périodicité ?

Simplement parce que la détection de cette périodicité se trouve très au-delà des puissances de calcul disponible et que par construction, elle le restera toujours.

4 Notion de nombre pseudo-premier
Attaquer la séquence des nombres premiers de front est une tâche trop complexe puisque que l’on se heurte immédiatement à la notion d’infini. Dans un premier temps, pour simplifier l’approche je vais définir une nouvelle notion : « Les pseudo-premiers de niveau n ».

4.1 Définition
Un nombre est appelé « pseudo-premier de niveau n » s’il n’est divisible par aucun des nombres premiers inférieurs ou égaux à n et est lui-même supérieur à n. Avec n premier.

4.2 Exemples
11 est un pseudo-premier de niveau 3 car il n’est pas divisible par 2 ni par 3. C’est également un nombre premier.
25 est un pseudo-premier de niveau 3 car il n’est pas divisible par 2 ni par 3. Mais ce n’est pas un nombre premier car il est divisible par 5. (25 n’est donc pas un pseudo-premier de niveau 5).

4.3 Construction
Il est facile de définir la liste des pseudo-premiers de niveau n pour une valeur de n particulière en procédant par soustraction.

4.3.1 Exemple des pseudo-premiers de niveau 2
Les pseudo-premiers de niveau 2 correspondent à tous les nombres non divisibles par 2. L’ensemble des pseudo-premiers de niveau 2 correspond donc à l’ensemble des nombres non multiple de 2.
Soit ℕ l’ensemble des entiers naturels. Notons l’ensemble des nombres entiers naturels multiple de 2. Notons l’ensemble des pseudo-premiers de niveau 2.

= ℕ –

La liste des nombres de l’ensemble est une liste périodique de période 2. Il s’agit de la liste des multiples de 2 : {2 4 6 8 10 12 14 16…}

4.3.2 Détermination de la longueur de la séquence périodique de construction
La longueur de la séquence périodique de est de 1 puisqu’une seule valeur est nécessaire pour la définir, la valeur +2. Une fois que l’on connait cette séquence périodique on peut trouver tous les éléments de l’ensemble par simple reproduction.

Exemple : A partir du premier élément de : {2} on applique la séquence périodique +2 et on obtient 4. On continue, à partir de 4 on applique +2 et on obtient 6 et ainsi de suite. On peut trouver ainsi l’ensemble des éléments de .
L’ensemble des pseudo-premiers de niveau 2 correspond par définition à la différence entre ℕ et soit : {3 5 7 9 11 13 15…}
La longueur de la séquence périodique de est de 1 puisque une seule valeur est nécessaire pour la définir, la valeur +2. Une fois que l’on connait cette séquence périodique on peut trouver tous les éléments de l’ensemble par simple reproduction.

Exemple : A partir du premier élément de : {3} on applique la séquence périodique +2 et on obtient 5. On continue, à partir de 5 on applique +2 et on obtient 7 et ainsi de suite. On peut trouver ainsi l’ensemble des éléments de .

4.3.3 Déduction :
Etant donné que est périodique par définition, que ꓴ = ℕ et que ꓵ = Ø
On en déduit que est périodique.

4.3.4 Exemple des pseudo-premiers de niveau 3
Notons l’ensemble des nombres entiers naturels multiples de 2 et/ou de 3. Notons l’ensemble des pseudo-premiers de niveau 3.
= ℕ –

La liste des nombres de l’ensemble est construit suivant une séquence périodique de période 6. Il s’agit de la liste des multiples de 2 et/ou de 3 : = {2 3 4 6 8 9 10 12 14 15 16 18 20 21 22 24 26…}

La longueur de la séquence périodique de construction de est de 4 puisque 4 valeurs sont nécessaires pour la définir, les valeurs {+1, +1, +2, +2}. Une fois que l’on connait cette séquence périodique on peut trouver tous les éléments de l’ensemble par simple reproduction.

Exemple : A partir du premier élément de : {2} on applique la séquence périodique +1 et on obtient 3. On continue avec +1 et on obtient 4. On applique +2 et on obtient 6, puis +2 et on obtient 8. A partir de là on peut recommencer la séquence périodique avec +1 et on obtient 9 et ainsi de suite. On peut trouver ainsi l’ensemble des éléments de .
L’ensemble des pseudo-premiers de niveau 3 correspond par définition à la différence entre ℕ et soit : {5 7 11 13 17 19 23 25…}
La longueur de la séquence périodique de est de 2 puisque deux valeurs sont nécessaires pour la définir, les valeurs {+2, +4}. Une fois que l’on connait cette séquence périodique on peut trouver tous les éléments de l’ensemble par simple reproduction.

Exemple : A partir du premier élément de : {5} on applique la séquence périodique +2 et on obtient 7. On continue, à partir de 7 on applique +4 et on obtient 11. A partir de là on peut recommencer la séquence périodique avec +2 et on obtient 13 et ainsi de suite. On peut trouver ainsi l’ensemble des éléments de .

4.4 Cas général : pseudo-premier de niveau n
Soit l’ensemble des pseudo-premiers de niveau n.
Soit = ℕ -
est donc l’ensemble des nombres multiples de 2 et/ou de 3 et/ou de 5 … et/ou de n.

4.4.1 Déduction
étant construit par addition d’ensembles de constructions périodiques, est également un ensemble possédant une séquence de construction périodique. La période de est d’autant plus grande que n est grand. On en déduit que possède également une séquence de construction périodique pour n fini.

4.4.2 Détermination de la longueur de la séquence périodique
La longueur de la séquence périodique de construction (notée LSP) peut se déterminer à l’aide d’une fonction à partir de la longueur de la séquence périodique précédente.

Exemple : Calculons les longueurs des séquences périodiques pour et , les ensembles des pseudo-premiers de niveau 5 et 7.
. (5-1) = 2 x 4 = 8
. (7-1) = 8 x 6 = 48
A l’aide de cette fonction on peut calculer le tableau suivant :


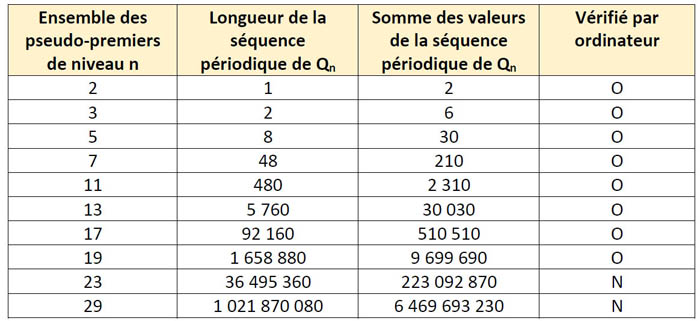
Le tableau montre que la longueur de la séquence périodique augmente de manière exponentielle avec la valeur de n. On dépasse le milliard dès la valeur 29 !
Par exemple pour l’ensemble des nombres pseudo-premiers de niveau 19 il faut dérouler une séquence de
1 658 880 termes pour retomber sur la même séquence.

Si on réalise la somme de toutes les valeurs constituant une séquence périodique, on constate que cette somme équivaut à la somme précédente multipliée par la valeur n du niveau calculé.
Notons les i valeurs de la séquence périodique de niveau n.
Pour i = 1 à : Σ = Σ x n

4.5 Détermination des valeurs de chaque séquence périodique
Si nous pouvions trouver une fonction nous permettant de déduire les valeurs d’une séquence périodique à partir des valeurs de la séquence précédente, cela nous rapprocherait d’une éventuelle formule des nombres premiers. Mais cela ne suffirait pas, il faudrait également trouver le moyen de rendre générale et synthétique cette fonction pour trouver directement les valeurs d’une séquence donnée sans être obligé de calculer toutes les séquences précédentes.

4.5.1 Analyse des premières séquences
L’analyse des premières séquences nous donne des informations sur la manière dont se constitue ces séquences périodiques.

Prenons l’exemple de la séquence de construction de niveau 7 () :
La = 8 on peut donc calculer : .(7-1) = 8 x 6 = 48
Comment se forme cette séquence de 48 valeurs ?
Cette séquence se forme par répétition de 7 fois la . 7 correspondant à la valeur du niveau de la SP en cours de réalisation : 8 x 7 = 56
Nous trouvons en réalité une longueur de séquence de 48 valeurs soit 8 de moins. Cela est du au fait que lors de la répétition de n fois la séquence précédente (7 fois dans notre exemple) il y a toujours agglomération par addition de deux valeurs adjacentes et cela un nombre de fois égale à la longueur de la séquence précédente :
Nous avions déjà vu que : .(n-1)
Nous savons désormais que correspond à la répétition de n fois avec agglomération par addition d’un certain nombre de valeurs adjacentes dans la séquence.
Notons « » ce nombre d’agglomérations pour le niveau n, il est possible de le calculer ainsi :
= (n x ) – =

provient de n fois avec agglomérations de données adjacentes.

4.5.2 Exemple de constitution d’une séquence périodique
Pour mieux comprendre prenons un exemple visuel, soit l’ensemble des pseudo-premiers de niveau 3 : {5 7 11 13 17 19…}
La séquence périodique de l’ensemble est : 2 4
(Rappel : 5 + 2 = 7 + 4 = 11 + 2 = 13 + 4 = 17 + 2 = 19…)
Construisons la séquence périodique de l’ensemble à partir de celle de :
On part de la 2ème valeur de la séquence précédente et on applique n fois, soit 5 fois la séquence précédente, on obtient : 4 2 4 2 4 2 4 2 4 2
Soit 10 valeurs. Il y a 2 valeurs de trop par rapport aux valeurs attendus via la fonction :
.(5-1) = 2 x 4 = 8
Il faut en effet agglomérer deux valeurs adjacentes : = 2 4 2 4 2 4 2 4 2 4 2
Pour obtenir : 4 2 4 2 4 6 2 6
Qui est bien la séquence périodique de :
= {7 11 13 17 19 23 29 31 37 41 43 47 49…}
7+4=11+2=13+4=17+2=19+4=23+6=29+2=31+6=37 + 4=41+2=43+4=47+2=49…

4.5.3 Horizon de validité des nombres premiers via les pseudo-premiers
Essayons de déterminer l’horizon de validité des nombres premiers à partir des pseudo-premiers d’un niveau arbitraire n.
On constate qu’un ensemble contient uniquement des nombres premiers jusqu’à la valeur (n+1)²-1.

Exemple : pour le premier nombre de cet ensemble qui ne soit pas premier est 49, ce qui correspond à 7². Pour le premier nombre de cet ensemble qui ne soit pas premier est 121, ce qui correspond à 11².
Horizon de validité de est : (n+1)²-1

Reprenons notre tableau et comparons avec cet horizon de validité :


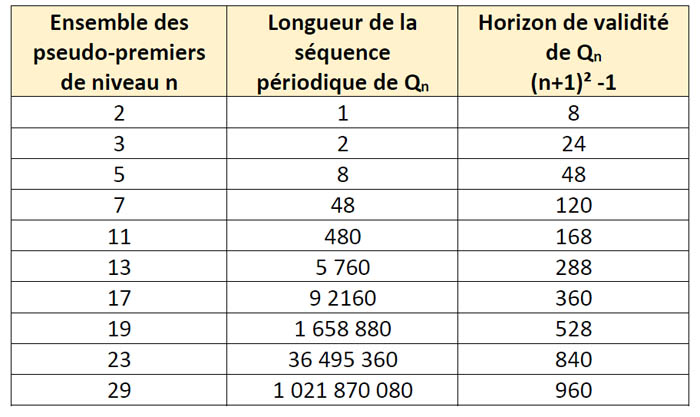
On remarque que l’horizon de validité des ensembles progresse de manière beaucoup moins rapide que la longueur de la séquence périodique qu’il faut connaitre pour pouvoir anticiper la séquence des nombres pseudo-premiers.

4.5.4 Conclusion intermédiaire
Dès le niveau 11, la séquence périodique de construction est plus longue que l’horizon de validité, cela démontre qu’il n’est pas possible d’anticiper la séquence des nombres pseudo-premiers et cela même si nous trouvons la fonction qui permet de déterminer directement la séquence périodique d’un niveau n.

4.6 Analyse de Qn quand n tend vers l’infini
La longueur de la séquence de périodicité des nombres premiers est donc gigantesque. De plus comme le nombre de nombres premiers est infini, il ne nous est pas possible de faire le calcul pour n infini.
Lorsque n tend vers l’infini tend vers ℕ et donc :
= ℕ - = ℕ - ℕ = Ø
Lorsque n est infini les pseudo-premiers n’existent plus.

4.7 Notion de multiples composés
Pour pallier ce problème définissons une nouvelle notion, la notion de multiples composés et appelons l’ensemble des multiples composés de 2. Un nombre est dit « multiple composé de n » s’il est le produit d’au moins deux fois n.
= {4 6 8 10 12 14 16 18 20 22…} La valeur 2 ne fait pas partie de car 2 n’est composé de 2 qu’une seule fois.
Appelons l’ensemble des pseudo-premiers généraux de niveau n.
Un nombre est appelé « pseudo-premier général de niveau n » s’il n’est divisible par aucun des nombres premiers inférieurs ou égaux à n. Avec n premier.

peut se construire de la sorte :
= ℕ -
= {2 3 5 7 9 11 13 15 17 19 21…}

4.7.1 Exemple avec
Soit l’ensemble des multiples composés de 2 et/ou de 3.
= {4 6 8 9 10 12 14 15 16 18 20 21 22 24 26…}
= ℕ -
= {2 3 5 7 11 13 17 19 23 25…}

4.8 Analyse de quand n tend vers l’infini
Lorsque n tend vers l’infini, Rn tend vers l’ensemble des nombres premiers P :
= ℕ - = P Lorsque n est infini l’ensemble des pseudo-premiers généraux devient l’ensemble P des nombres premiers.

La longueur de la séquence périodique de quand n est infini est égale au nombre d’éléments de .
On en déduit que la longueur de la séquence périodique de P est égale au nombre d’éléments de P. Cette séquence n’étant reproduite qu’une fois, P n’est donc pas périodique. La conjecture annoncée au début de cette réflexion est donc fausse.

5 Conclusion générale
La séquence des nombres premiers n’est pas construite en suivant une séquence de construction périodique. Aucune fonction ne peut permettre de trouver, sans un calcul itératif, la valeur d’un nombre premier à une position arbitraire n.

[LB2]

Bonjour Thierry,

c'est intéressant, je vais lire ces raisonnements. Attention dès le début à ne pas confondre deux choses différentes :

- une fonction qui donnerait TOUS les nombres premiers. Autrement dit, une énumération de l'ensemble des nombres premiers.

- une fonction telle que est premier.

De plus, attention à ne pas confondre fonction et formule : une fonction peut être définie par récurrence, sans formule explicite pour calculer , par exemple.

La formule (Euler) donne des nombres premiers pour
voir par exemple
https://fr.wikipedia.org/wiki/Formules_ ... s_premiers
pour des résultats intéressants

Cordialement

[LB2]

Les analyses statistiques réalisées sur les premiers milliards des nombres premiers laissent à penser que les nombres premiers apparaissent de manière quasi aléatoire, aucune séquence logique ne semble visible dans cette liste.

Cette affirmation est vague, que signifie-t-elle exactement?

"apparaitre de manière aléatoire" n'a pas de sens mathématique, alors "quasi-aléatoire" ...

Quand on parle d'aléatoire, il faut un modèle et souvent on parle de lois de probabilités : uniforme, exponentielle, normale, binomiale...

On s'est intéressé à la répartition des nombres premiers, par exemple au nombre de nombres premiers entre 1 et n (en tout cas, à un équivalent asymptotique de ce nombre). Ce résultat est connu sous le nom de "théorème des nombres premiers" de Hadamard et La Vallée Poussin, mais c'est un résultat difficile (niveau L3/M1)
http://images.math.cnrs.fr/Jacques-Hada ... oreme.html

Un autre énoncé intéressant est le théorème de la progression arithmétique de Dirichlet : si et sont deux entiers premiers entre eux, alors il existe une infinité de nombres premiers de la forme , avec entier.

C'est également un résultat difficile (niveau L3/M1)

Bien cordialement

[LB2]

Je crois qu'il est assez facile de montrer que la troisième colonne de ton premier tableau (que tu as appelée "somme des valeurs de la séquence périodique de Qn") est la suite ppcm(2,3,5,7,...,p_n)=2*3*5*7*...*p-n où p_n est le n-ième nombre premier. C'est à dire le produit des nombres premiers jusqu'à p_n.

[Ben314]

Salut,
On va essayer de regarder dans l'ordre :

(1) Depuis toujours les mathématiciens ont cherché en vain une fonction qui permettrait de donner directement le nième nombre premier. Appelons « f » cette hypothétique fonction...
Déjà, là c'est pas ça du tout le problème : la fonction f qui à l'entier n associe le n-ième nombre premier existe et n'est absolument pas "hypothétique". Sa définition c'est tout bêtement la phrase en rouge çi dessus qui est on ne peut plus mathématique et sans la moindre ambiguïté. Par contre, ce qu'on ne sait pas faire/écrire, c'est trouver un moyen simple et rapide de calculer la valeur de f(n), plus précisément moyen autre qu'en dressant la liste des nombres premiers jusqu'au n-ième (ce qui est évidement faisable, en particulier avec un ordinateur, mais... long...). Bref, ce qu'on peut éventuellement chercher concernant cette fonction f, c'est un algorithme "assez rapide" pour calculer f(n) (en précisant bien sûr ce que signifie "assez rapide") et en conséquence, c'est plutôt un truc à cheval entre les maths. et l'informatique (recherche d'algorithme).

(2) (2) Les analyses statistiques réalisées sur les premiers milliards des nombres premiers laissent à penser que les nombres premiers apparaissent de manière quasi aléatoire, aucune séquence logique ne semble visible dans cette liste.
Ça, on peut pas dire que c'est franchement faux vu qu'il faudrait clairement définir précisément ce que signifie "quasi aléatoire" mais c'est quand même franchement très très loin de représenter la vérité (*) :
- Déjà, il est clair qu'à part 2, tout les nombres premiers sont impairs, qu'à part 2 et 3, ils sont tous congrus à 1 ou 5 modulo 6, etc etc et ça (par exemple), il me semble que ça dit bien que c'est pas du tout aléatoire, non ?
- On a conjecturé très tôt et on sait démontrer aujourd'hui (pas facile du tout) qu’asymptotiquement, f(n) est équivalent à n*ln(n).

(*) Pour moi, c'est exactement le type de phrase qu'on trouve souvent dans les mauvais livres de vulgarisation pour "faire mousser" le sujet. Et à part d'énerver les lecteurs qui connaissent un peu le sujet, ça ne sert à rien.

(3) Il a été prouvé que le nombre de premiers jumeaux est infini.
Non : pour le moment on n'a rien prouvé du tout et c'est une simple conjecture.

(3) ... je poserai la conjecture suivante :
La séquence de construction des nombres premiers est périodique. Elle est périodique par définition.
Ça, déjà, c'est "du grand n'importe quoi" au niveau logique : comment veut-tu qu'un truc comme la suite des nombres premiers, donc déjà défini, soit périodique "par définition". Est ce que ça te viendrait à l'esprit de dire par exemple que "35 est pair par définition" ?
Vu que 35 est un nombre parfaitement bien défini et que le fait d'être pair est aussi parfaitement bien défini, ben l'assertion "35 est pair", elle est soit vraie, soit fausse, mais sûrement pas "par "définition".
Donc, déjà, le fait que la suite des nombre premier est périodique, c'est vrai ou c'est faux, mais sûrement pas "par définition".
Et en l’occurrence, c'est très facile de montrer que c'est faux : s'il y avait une période P, alors, partant d'un nombre premier donné, tout les nombre de la forme (avec ) devraient être premier. Or si on prend on a qui n'est pas premier.


P.S. J'ai non seulement pas tout lu (ce que j'ai lu m'a suffit pour me faire une idée...), mais j'ai pas regardé non plus les réponses....

P.S.2 : En regardant en diagonale la suite, ce que tu fait, ton truc, ça s'appelle la méthode du crible d’Ératosthène (<-lien) et c'est effectivement une très bonne méthode pour trouver la liste des nombres premiers inférieurs à une barre donnée (mais c'est bien connu depuis au moins le 3em siècle avant Jésus-Christ...)

[Pseuda]

Bonjour,

Je n'ai pas tout lu non plus, mais juste une petite remarque : ils parlent de la séquence de construction qui est périodique (pas de la séquence elle-même). Encore faut-il savoir ce qu'est une séquence de contruction périodique...

[Ben314]

Effectivement, j'ai pas regardé la conclusion :
La séquence des nombres premiers n’est pas construite en suivant une séquence de construction périodique. Ça, si c'est sensé vouloir dire que la suite des nombre premier n'est pas périodique, alors , c'est effectivement O.K. (mais bon, normalement on le prouve en une ligne et pas en 4 pages...)

Aucune fonction ne peut permettre de trouver, sans un calcul itératif, la valeur d’un nombre premier à une position arbitraire n.
Là, par contre, je vois pas le rapport avec la choucroute : le fait qu'il n'y ait pas de période, ça prouve évidement pas qu'il n'y a pas d'algo. non récursif pour calculer F(n). Par exemple F(n)=n², c'est pas franchement périodique et pourtant, ça se calcule on ne peut mieux non récursivement.

[nodgim]

Il se sert de la périodicité des multiples des nombres premiers pris dans l'ordre.
2 a une période 2, les pairs sont éliminés, le premier non éliminé est 3.
On élimine les multiples de 3, la périodicité des multiples de 2 et 3 est 2 * 3 = 6. Ne reste dans une période 6 que 2 nombres premiers (pseudo premiers dans son vocabulaire).

Et effectivement avec cette méthode on construit des tableaux successifs :

5
7

pour une période 6 (évidemment on a éliminé le 3 )

On copie 4 fois (5,7) en ajoutant 6 à chaque colonne :

5 11 17 23 29
7 13 19 25 31

On élimine les multiples de 5 (On montre facilement qu'on élimine exactement un nombre par ligne), reste dans la période 30 = 2 * 3 * 5 : (2-1)*(3-1)*(5-1)= 8 nombres.

On ajoute 6 colonnes (parce que 7 est le nombre premier suivant) en ajoutant 30 au nombre de la colonne précédente :

7 37 67 97 127 157 187
11 41 71 101 131 161 191
13 43 73 103 133 163 193
17 47 77 107 137 167 197
19 49 79 109 139 169 199
23 53 83 113 143 173 203
29 59 89 119 149 179 209
31 61 91 121 151 181 211

Etc.....


Si on ne fait pas attention avec cette construction, on a l'intuition immédiate (mais fausse) que les premiers jumeaux sont en quantité infinie.

[Thierry39]

Bonjour et merci beaucoup pour vos réponses.
Comme je vous le disais je ne suis pas mathématicien et j'ai écris quelques bourdes !

Concernant les remarques de LB2, OK je suis d'accord. Je suis d'accord également avec mon imprécision concernant le "Quasi-aléatoire" qui est bien expliqué par Ben314.
Idem quand Ben314 explique que la fonction f(n) existe forcément mais qu'on ne sait pas la trouver, je suis d'accord, c'est un manque de rigueur de ma part dans la manière de m'exprimer.

(3) Il a été prouvé que le nombre de premiers jumeaux est infini.
Non : pour le moment on n'a rien prouvé du tout et c'est une simple conjecture.
OK je ne savais pas, je pensais avoir lu que c'était prouvé.

Concernant la remarque de Ben314 sur le "Par définition", oui comme le précise Pseuda, je ne parle pas de la séquence des nombres premiers mais de leur séquence de construction. Comme les nombres premiers sont des nombres qui ne sont pas des multiples et que la séquence de construction des multiples est périodique (du moins je le pense), par soustraction il me semble "automatique" que la séquence de construction des nombres premiers doit être périodique. A la fin de mon exposé, j'arrive cependant au fait que cette séquence de construction n'étant présente qu'une seule fois, elle n'est pas périodique !

Concernant la précision de Ben314 au sujet de la phrase :
Aucune fonction ne peut permettre de trouver, sans un calcul itératif, la valeur d’un nombre premier à une position arbitraire n.
Ben 314 : "Là, par contre, je vois pas le rapport avec la choucroute : le fait qu'il n'y ait pas de période, ça prouve évidement pas qu'il n'y a pas d'algo. non récursif pour calculer F(n). Par exemple F(n)=n², c'est pas franchement périodique et pourtant, ça se calcule on ne peut mieux non récursivement".
Je reconnais que c'est un peu rapide ! Ce que je veux dire, c' est que si la séquence de construction des nombres premiers n'est pas périodique (cas des pseudo-premiers de niveau n quand n est infini) il est impossible de trouver la fonction F(n).
Pour l'exemple F(n)=n² : il suffit d'ajouter 2 à la précédente valeur ajoutée, pour retrouver la séquence.
1 4 9 16 25 36 correspond à : +3 + 5 +7 +9 +11

Je reconnais que ça reste flou, je vais creuser l'idée en faisant attention à vos remarques.

[Ben314]

Ce que je veux dire, c' est que si la séquence de construction des nombres premiers n'est pas périodique (cas des pseudo-premiers de niveau n quand n est infini) il est impossible de trouver la fonction F(n).
Pour l'exemple F(n)=n² : il suffit d'ajouter 2 à la précédente valeur ajoutée, pour retrouver la séquence.
1 4 9 16 25 36 correspond à : +3 + 5 +7 +9 +11

Ben oui, c'est effectivement "on ne peut plus flou", voire même à mon avis franchement dénué de sens :
- Déjà, LA séquence de construction des nombres premiers, ça veut rien dire : les nombre premiers, c'est une partie de N et il y a bien entendu des tonnes de façon de la construire. Si tu préfère, on peut dire ça sous la forme qu'il existe des tonnes de critères de primalités plus ou moins rapides.
- Ensuite, j'espère quand même que tu te rend compte que d'écrire un truc du style "quand n est infini" c'est bien évidement totalement dépourvu du moindre sens : des "entiers infinis", il n'y en a pas (dans la théorie usuelle des entiers). La notions d'infini qu'on utilise en math., en particulier dans les limites, ça traduit uniquement un comportement asymptotique lorsque n devient de plus en plus grand (le fameux "quelque soit-il existe" des définitions) mais l'infini, en temps que nombre, ça me semble quand même on ne peut plus évident que ça n'existe pas (va demander à ton épicier une infinité de nouilles pour voir ce qu'il en pense...).
Donc si on parle d'infini, tout ce qu'on peut faire, c'est de "tendre vers l'infini" et, lorsqu'à chaque entier on associe un "quelque chose", ben il faut évidement préciser ce que l'on entend par "tendre vers" sur l'ensemble des "quelque chose" si on veut pouvoir parler de limite. Bref, dans un cas comme ici, tu peut éventuellement faire tendre n vers l'infini, mais il faudrait évidement que tu précise quelle définition tu donne au fait "qu'une suite de séquence tende vers une séquence" vu qu'il n'y a aucune définition mathématique dédiée.
- Le "il est impossible de trouver la fonction F(n)" c'est toujours autant archi faux. Donc je redit ce que j'ai déjà dit, à savoir que dans n'importe quel langage de programmation, aussi rudimentaire soit il, on peut parfaitement programmer une fonction F qui, lorsqu'on lui donne en entrée la valeur de N, donne en réponse la valeur du N-ième nombre premier. Le seul problème, c'est que si N est "relativement grand", en l'état actuel des connaissances, ça va être "relativement long" pour avoir la réponse.
- Concernant la fonction F(n)=n², je ne comprend pas le sens de ta remarque : Si j'ai mis cet exemple, c'est uniquement (et exclusivement) pour que tu réponde à ces trois questions :
* Est-elle périodique OUI/NON ?
* Est-elle rapide à calculer OUI/NON ?
* Que peut on en déduire concernant l'implication "Non Périodique => Non rapide à calculer" ?
Parce que si c'est uniquement pour signaler que les fonctions F(n)="n-ième nombre premier" et F(n)=n² ne sont pas identiques, ben ça je pense que tout le monde le savait.

[Thierry39]

Bonjour,
je précise mon idée et je répond à Ben314.

La séquence des nombres premiers semble très complexe, or en réalité il ne s'agit que de la différence entre ℕ et la séquence des nombres multiples, cette dernière étant bien connue tant que le nombre de multiples pris en compte est fini. Ce que j'essaie de faire est d'approcher la séquence des nombres premiers par différence de ℕ et de la séquences des nombres multiples, quand n (le nombre de multiples pris en compte) tend vers l'infini.

Quand tu dis qu'il y a un grand nombre de façon de construire la séquence des nombres premiers, peut-être, mais dans mon cas je me concentre sur une seule : l'ajout successif de nombres entiers de proche en proche.

Ce que j'appelle "séquence de construction périodique", c'est la suite des entiers qu'il faut additionner pour passer aux occurrences suivantes. Le terme de périodique n'est pas à comprendre comme dans le cas d'une fonction périodique. Dans mon cas il signifie que la longueur de la séquence de construction est finie et que pour continuer à trouver la séquence recherchée il suffit de repartir au début de cette séquence de construction, de boucler en quelque sorte.
Si on prend l'exemple des pseudo-premiers de niveau 3 noté Q (c'est à dire les nombres qui ne sont pas divisibles par 2 ni par 3) : {5 7 11 13 19 23 25...}
La longueur de la séquence périodique de Q est 2 et elle est définie par les valeurs {+2, +4}.
En faisant 5+2+4+2+4+2 etc.. on trouve toute la séquence.
Pour les pseudo premier de niveau 19 c'est la même chose sauf que la séquence de construction périodique à une longueur de 1 658 880. C'est à dire qu'il faut atteindre le 1 658 880 ème nombre pseudo-premier de niveau 19 pour boucler sur la même séquence. Cette longueur de séquence est énorme par rapport à la faible valeur du niveau 19. Cela explique à mon avis pourquoi la séquence des nombres premiers est difficilement compréhensible.
On voit très bien que quelque soit la valeur de n que l'on choisira, on trouvera que la séquence de construction des pseudo-premier de niveau n est périodique. On voit donc que quand n tend vers l'infini la séquence de construction est toujours périodique. La séquence des nombres premiers correspond à la séquence des pseudo-premiers de niveau n, avec n infini. Comme tu l'expliques bien dans ta remarque, il n'est pas permis de donner la valeur infini à un entier. Cela signifie que nous sommes obligés de travailler avec un n fini et donc nous restons tributaire de l'horizon de validité qui est fixé à (n+1)² -1.

Ta remarque indiquant qu'il n'est pas permis de réfléchir avec un entier égal à l'infini mais uniquement qui tend vers l'infini est juste.
Je corrige donc l'expression :
"La longueur de la séquence périodique de quand n est infini est égale au nombre d’éléments de .
On en déduit que la longueur de la séquence périodique de P est égale au nombre d’éléments de P. Cette séquence n’étant reproduite qu’une fois, P n’est donc pas périodique. La conjecture annoncée au début de cette réflexion est donc fausse."
Par :
"La longueur de la séquence périodique de R quand n tend vers l'infini tend vers le nombre d’éléments de .
On en déduit que la longueur de la séquence périodique de P est égale au nombre d’éléments de P. Cette séquence n’étant reproduite qu’une fois, P n’est donc pas construit suivant une séquence de construction périodique. La conjecture annoncée au début de cette réflexion est donc fausse."

[Ben314]

Bon, pour commencer, j'ai l'impression que le truc auquel tu veut en venir c'est de démontrer que l'ensemble des nombre premiers n'est pas périodique où la notion "d'ensemble périodique" et bien celle dont tu parle.
Et c'est bien avec cette notion là qu'on prouve en une ligne (c.f. quelque posts plus haut) que l'ensemble des nombres premiers n'est pas périodique.

Ensuite, ta preuve contient plusieurs lacunes :
(1) Tu dit que "la" période de l'ensemble des entiers non divisible par 2, ni par 3, ni par 5, ... ni par p c'est le ppcm de 2,3,5,...,p alors qu'autant il est bien évident que c'est UNE période, autant c'est pas super clair que c'est effectivement LA période (i.e. la plus petite possible).
(2) Jusque là, c'est pas très grave (vu qu’effectivement, avec un petit effort de raisonnement on arrive à montrer que c'est bien LA période), mais par contre, ton "passage à la limite" pour passer de tes ensembles Qn à P, ce n'est que de la "pure conjecture" sans le début de la moitié d'une preuve.
Il faut bien comprendre que l'infini, c'est une pure "vue de l'esprit" totalement abstraite donc pour laquelle il n'y a absolument rien "d'évident" et, par exemple, le fait que les périodes des Qn soient de plus en plus grande, si tu veut en déduire que leur intersection infinie (à savoir P) n'a pas de période, il faut forcément produire une vrai preuve et sûrement pas faire comme si c'était "une évidence".

[Thierry39]

Je te remercie pour cette réponse.
Je suis d'accord, je vais réfléchir.

[Rdvn]

Bonjour,
pour avancer dans votre démarche, voici un livre très intéressant :
auteur : Jean-Paul Delahaye
titre : Merveilleux nombres premiers
éditeur : Belin - Pour la science
Cordialement
Rdvn