Déterminer l'équation de la courbe que l'on souhaite obtenir

[Simblizok]

Bonjour,

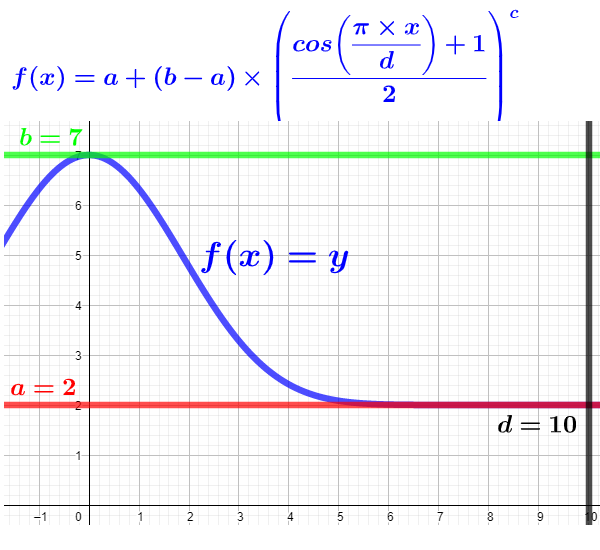
Pour un projet personnel, je cherche à déterminer une fonction à partir de l'idée de la courbe que je souhaite, et des paramètres dons j'ai besoin. Et je n'ai aucune idée de comment rétro-ingéniéré mon idée en une fonction dût notamment à mes lacunes et mon inexpérience en math. Je suis tout aussi intéressé par le cheminement que par la solution, merci d'avance si vous me donner directement la solution, mais je souhaites aussi en connaitre le cheminement!

Voila: je souhaite donc trouver la fonction qui réalise une courbe comme schématisé ci dessous (merci Paint) :



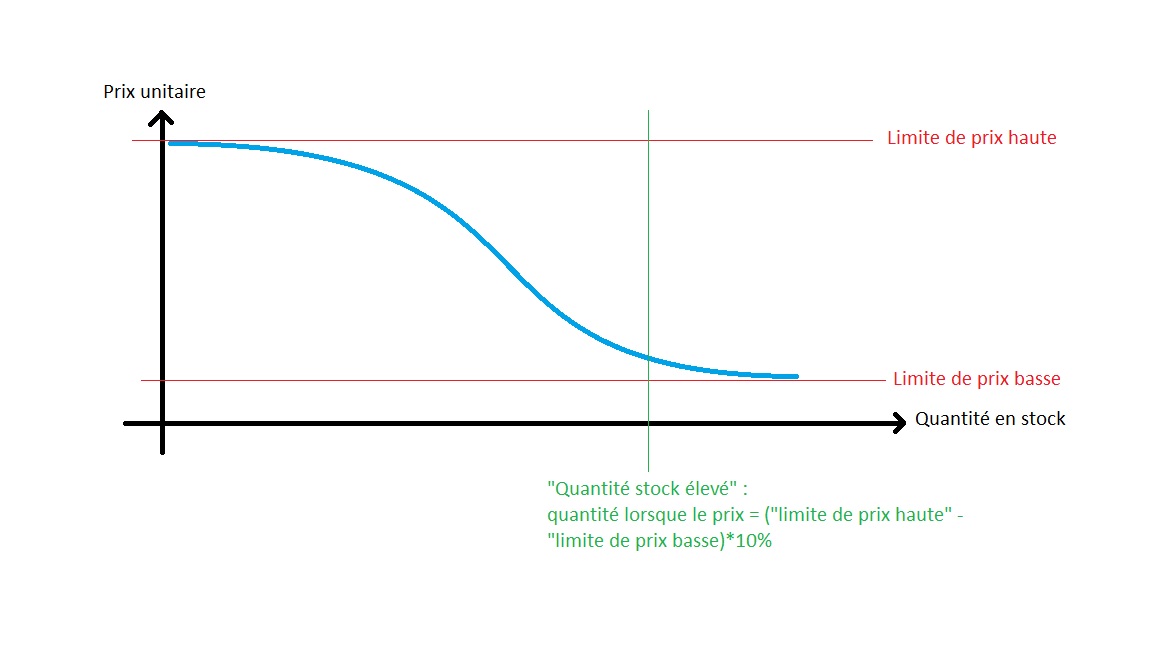
Dans cette fonction, je souhaites avoir au moins 3 facteurs de réglage :
-La limite haute + la limite basse vers lesquelles la courbe va tendre.
-Un facteur de compression que j'ai appelé ici "Quantité stock élevé" Qui me permettrai de compresser la courbe le long de l'axe des abscisses (mais après vous avez peut être plus malin à me proposer)

Je me moque de ce qui ce passe avant 0, mon système est limité par programmation, un stock ne peut être négatif. Comment puis-je procéder?

Merci de votre aide d'avance!
Simblizok

Ps: J'aurais pu utilisé une droite et limité via programmation mes limites haute et basse, mais ou serait le fun dans tout ça?

[azf]

Bonjour

Fonction à quatre paramètres et que vous pouvez modifier selon vos besoins
Vous n'en donnez que trois alors qu'il en faut quatre
1-limite haute du prix
2-limite basse du prix
3-facteur de compression
4-quantité limite de stock
Parce que j'imagine que dans la pratique un stock ne sera jamais infini
N'est-ce pas?

[Simblizok]

Bonjour

L'équation sera intégrée dans un "programme " la quantité limite de stock sera limitée par le code si besoin est. (Mais en théorie le stock sera "pseudo" infini, limité par le maximum d'une variable "double integer")

Car si la courbe s'arrête ou tombe à zéro une fois la limite atteinte le programme lui continuera à calculer quelque chose. Donc le facteur de quantité limite n'a pas besoin d'être intégré dans la fonction.

Par contre je suis intéressé de savoir si en sois c'est possible, juste par curiosité.

Cordialement,
Simblizok

[azf]

avec une limite maximale pour la quantité de stock pour quatrième paramètre, il y a une fonction extrêmement simple

Après tout un paramètre ça peut se modifier à sa guise

là pour facteur de compression j'ai pris

Une autre variante de la fonction est aussi possible en plaçant le facteur de compression en facteur ...
mais bon là il faudrait en savoir plus sur ce que vous voulez comme type de "facteur de compression"

[Vassillia]

Bonjour,
Si tu veux quelque chose de précis, on va avoir besoin de valeurs pour faire la régression la plus adaptée possible. Mais sinon, même si la proposition de azf est très bien, pour moi cela ressemble plus ou moins à une fonction logistique donc je peux te proposer cela



Avec
max = limite de prix haute
min = limite de prix basse
c est un coefficient qui peut servir de facteur de compression
d est un facteur pour décaler la courbe vers la droite ou vers la gauche

[azf]

Bonjour Vassillia, oui en fait ce que tu propose ressemble plus à ce qu'il recherche

[Simblizok]

Bonjour,

Merci à vous deux pour vos réponses! C'est effectivement la réponse de Vassillia qui convient parfaitement à mon application ! Chapeau l'artiste !

(Je ne pratique pas les maths dans la vie de tous les jours et j'étais du genre à me dire que les exponentiels ne me servirai jamais dans la vie. Je me suis trompé pour le coup. ^^)

[Vassillia]

Tant mieux et ravie d'avoir pu montrer que l'exponentielle peut servir
Bon courage pour ton application

[lyceen95]

J'aurais vu la fonction arctangente() ou atan()
- tu as besoin de définir le point d'inflexion ( le point de symétrie, le point à mi-hauteur entre les 2 asymptotes horizontales ... c'est le point intéressant. : X0 l'abscisse de ce point, et donc on aura un truc autour de y = atan(x-x0)
- tu as besoin de définir l'amplitude : l'écart entre les 2 droites horizontales : h ; et du coup : y = (h/2) atan(x-x0)
- a priori, tu veux que la droite du bas scorresponde ave la droite y=0 , donc : y = (h/2)( atan(x-x0)+1)

- Et tu peux jouer sur la vitesse de descente : est-ce que tu veux une pente plus ou moins abrupte, autour du point de symétrie x0 : c'est le paramètre k qui permettra de jouer : y = (h/2)( atan(k(x-x0))+1)

[azf]

Bonjour Vassillia et merci d'avance

Excusez moi ce petit aparté (l'auteur du sujet est parti je suppose ...enfin je l'espère là pour le coup)
Vassillia avec quoi as tu réalisé l'image pour ta fonction?
ça ne ressemble pas à Géogébra
Si ce n'est pas ça et sachant que tu est une professionnelle si jamais ce que tu utilise est gratuit et libre d'accès peux tu me placer un lien et parler un peu de cet outil (pour te dire la vérité j'en ai un peu marre de Géogébra)
Mais il est très possible vu que tu est une pro tu utilise un outil utilisé par les "pro" et du coup je resterai sur geogebra (je m'adapte)

[Vassillia]

Bonjour azf, je n'ai pas vraiment de préférence pour les sites en ligne qui tracent des fonctions, difficile de te conseiller sans savoir ce que tu cherches exactement en voici quelques-uns mais une recherche google t'en donnera surement d'autres :
https://calculis.net/fonction
https://www.codabrainy.com/traceur-de-courbes/
https://www.solumaths.com/fr/graphique- ... rbe/tracer

PS : j'enseigne les biostats, c'est très particulier comme branche, dire que je suis pro ne me parait pas très légitime, il y a des tas de domaines où je n'y connais pas grand chose (souvenir d'étudiante au mieux)

[azf]

Merci Vassillia

Je vais voir tout ça

PS: tu est modeste et c'est très louable mais je sais que tu est une sacrée tueuse de charlatans

[Simblizok]

Bonjour,

Je suis toujours la

Je donnes ici un outils de traçage de courbe que j'ai trouver en cherchant une solution de traçage de courbe :

https://www.desmos.com/calculator/2ile4gshgc

Ce lien vous mène sur les tracé des courbe que vous m'avez proposé.

@lyceen95 : La base de fonction que tu m'as donné ressemble aussi çà ce que je veux, mais le point d'inflexion semble être légèrement décalé de l avaleur souhaité, et plus la valeur souhaité est grande plus l'écart du point d'inflexion est éloigné de la valeur souhaité. De plus, travailler avec l'amplitude n'est pas exactement ce que je recherche. Mais merci d'avoir détaillé ton processus ta réponse reste intéressante

[azf]

Bonjour Slimblizok et merci pour le lien

L'amplitude et le point d'inflexion de la fonction de Lycéen peuvent se modifier

Il est préférable (et poliment plus correct) qu'il vienne te le montrer

[fatal_error]

hi @Simblizok

je suis pas sûr de comprendre si du coup tu as trouvé une fonction suffisament satisfaisante pour représenter ta courbe

si non, pe donne des couples (x;f(x)) pour qu'on puisse te proposer qqch de plus concret

arctan(lyceen), sigmoide(vassilia) semblent qd même pas mal

[Simblizok]

Bonjour,

Je reviens vers vous après plusieurs jours et quelque essai en "conditions réelles" ,a fonction proposé par Vassilia correspond a mon besoin.

Chose remarquable la fonction ne fonctionne pas très bien dans Google Sheet, pour des grandes valeurs de x il arrive sort un défaut "Résulta supérieur à 1.79 ,e+308 " Alors que techniquement c'est du 1/exp(710) donc ça tend vers 0. A mon avis, le problème vient de la façon d'on il résous ses calculs: Il réalise l'exponentiel et dépasse la capacité de ça variable et ne peu donc pas résoudre le reste du calcul.

Mais dans mon application ça fonctionne donc tout roule!

Le sujet est clos pour ma part. Encore merci!