Comment exprimer la hauteur d'une sphère tronquée en fonction de son volume
15 messages
- Page 1 sur 1
Comment exprimer la hauteur d'une sphère tronquée en fonction de son volume
Bonjour à tous,
Je suis nouveau sur ce forum et je sollicite votre aide.
J'ai besoins de calculer la hauteur d'une calotte sphérique en fonction de son volume et autres variables comme le rayon de la sphère ou encore le rayon de base de la calotte.
J'ai bien trouver la formule du volume d'une sphère tronquée mais celle ci est exprimée en fonction de sa hauteur h sous une forme que je n'arrive pas à factoriser de façon à isoler h.
Mon but est ensuite d'utiliser cette formule dans Excel donc je ne peux pas avoir de formule sous la forme d'une intégrale.
Je vous remercie par avance pour votre aide
Je suis nouveau sur ce forum et je sollicite votre aide.
J'ai besoins de calculer la hauteur d'une calotte sphérique en fonction de son volume et autres variables comme le rayon de la sphère ou encore le rayon de base de la calotte.
J'ai bien trouver la formule du volume d'une sphère tronquée mais celle ci est exprimée en fonction de sa hauteur h sous une forme que je n'arrive pas à factoriser de façon à isoler h.
Mon but est ensuite d'utiliser cette formule dans Excel donc je ne peux pas avoir de formule sous la forme d'une intégrale.
Je vous remercie par avance pour votre aide
E&EMA a écrit:Bonjour à tous,
Je suis nouveau sur ce forum et je sollicite votre aide.
J'ai besoins de calculer la hauteur d'une calotte sphérique en fonction de son volume et autres variables comme le rayon de la sphère ou encore le rayon de base de la calotte.
J'ai bien trouver la formule du volume d'une sphère tronquée mais celle ci est exprimée en fonction de sa hauteur h sous une forme que je n'arrive pas à factoriser de façon à isoler h.
Mon but est ensuite d'utiliser cette formule dans Excel donc je ne peux pas avoir de formule sous la forme d'une intégrale.
Je vous remercie par avance pour votre aide
Salut
le volume d'une calotte sphérique est donnée par:
Si tu veux h en fonction de V tu as une équation de degré 3 à résoudre
Modifié en dernier par chan79 le 30 Sep 2016, 08:12, modifié 1 fois.
Bonjour chan 79,
Je te remercie pour le temps que tu m'accordes.
Ce que je comprend par ta réponse c'est qu'il y a trois solution possible à l'equation et que je ne peux avoir une formule du type h=V*k ou k est un coefficient obtenu à partir des propriétés de la sphère.
Ais je bien compris ou peux tu dans le cas contraire me donner la formule sous cette forme afin que je puisse l'exploiter.
Merci d'avance pour ta réponse.
Je te remercie pour le temps que tu m'accordes.
Ce que je comprend par ta réponse c'est qu'il y a trois solution possible à l'equation et que je ne peux avoir une formule du type h=V*k ou k est un coefficient obtenu à partir des propriétés de la sphère.
Ais je bien compris ou peux tu dans le cas contraire me donner la formule sous cette forme afin que je puisse l'exploiter.
Merci d'avance pour ta réponse.
C'est à vérifier, mais à mon avis, en moins d'une dixaine d'itérations de la méthode des tangentes de Newton, tu va avoir une valeur trés précise de ton h.
Si il y a un truc de sûr et certain, c'est que h ne va pas dépendre linéairement de V !!!E&EMA a écrit:...je ne peux avoir une formule du type h=V*k ou k est un coefficient obtenu à partir des propriétés de la sphère.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
E&EMA a écrit:Bonjour chan 79,
Je te remercie pour le temps que tu m'accordes.
Ce que je comprend par ta réponse c'est qu'il y a trois solution possible à l'equation et que je ne peux avoir une formule du type h=V*k ou k est un coefficient obtenu à partir des propriétés de la sphère.
Ais je bien compris ou peux tu dans le cas contraire me donner la formule sous cette forme afin que je puisse l'exploiter.
Merci d'avance pour ta réponse.
Par exemple pour R=10 et V=30
la seule solution qui convient est proche de 1
Modifié en dernier par chan79 le 30 Sep 2016, 08:13, modifié 2 fois.
Merci quand même
Je vous remercie pour toutes vos réponses qui ne m'ont toutefois pas aidées à compiler mon problème dans Excel.
Merci quand même pour votre temps.
Merci quand même pour votre temps.
Sans vouloir être "pédant", ça m'a pris environ 3 minutes à mettre en place :
https://drive.google.com/file/d/0ByyHQqLyqzSuWXh4NHQ1RnZlQVE/edit?usp=sharing
Mode d'emploi : tu rentre R puis V (qui doit être inférieur à 4/3 pi R^3) et ça te donne h ainsi que pi/3(3Rh²-h³) (pour vérif)
https://drive.google.com/file/d/0ByyHQqLyqzSuWXh4NHQ1RnZlQVE/edit?usp=sharing
Mode d'emploi : tu rentre R puis V (qui doit être inférieur à 4/3 pi R^3) et ça te donne h ainsi que pi/3(3Rh²-h³) (pour vérif)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Comment exprimer la hauteur d'une sphère tronquée en fon
Bonjour. La réponse analytique est h(V) = r (1 + 2 cos((acos(1 - 3V/(2πr³)) + 4π )/3))
Re: Comment exprimer la hauteur d'une sphère tronquée en fon
Bonjour,
Voici une relation à tester sur excel :
h = (sqrt(3) sqrt(3 V^2-4 π R^3 V)+2 π R^3-3 V)^(1/3)/(2 π)^(1/3)+((2 π)^(1/3) R^2)/(sqrt(3) sqrt(3 V^2-4 π R^3 V)+2 π R^3-3 V)^(1/3)+R
Voici une relation à tester sur excel :
h = (sqrt(3) sqrt(3 V^2-4 π R^3 V)+2 π R^3-3 V)^(1/3)/(2 π)^(1/3)+((2 π)^(1/3) R^2)/(sqrt(3) sqrt(3 V^2-4 π R^3 V)+2 π R^3-3 V)^(1/3)+R
Re: Comment exprimer la hauteur d'une sphère tronquée en fon
salut
En latex, ça fait quoi ?
Sinon pas de souci pour la réponse de MONSTRE. C'est la formule de Cardan. Simplement, il ne faut pas oublier le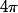 car il y a 3 solutions et il faut donner la bonne.
car il y a 3 solutions et il faut donner la bonne.
En latex, ça fait quoi ?
Sinon pas de souci pour la réponse de MONSTRE. C'est la formule de Cardan. Simplement, il ne faut pas oublier le
Re: Comment exprimer la hauteur d'une sphère tronquée en fon
anthony_unac a écrit:Sauf erreur,
y'a un petit souci; sous les racines, après factorisation de 3V, tu as
V est inférieur au volume de la sphère de rayon R.
Re: Comment exprimer la hauteur d'une sphère tronquée en fon
Votre remarque est pertinente 
Du coup je commence sérieusement à m'interroger sur cette solution proposée par Wolfram ?

Du coup je commence sérieusement à m'interroger sur cette solution proposée par Wolfram ?
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
