En cheminant avec Kakeya
60 messages
- Page 1 sur 3 - 1, 2, 3
En cheminant avec Kakeya
Un tour des mathématiques pour un tour d'aiguille : [url="http://math.univ-lyon1.fr/~borrelli/Kakeya/En_cheminant_avec_Kakeya.pdf"]En cheminant avec Kakeya[/url]
Conseillé à tous.
:happy3:
Conseillé à tous.
:happy3:
Alors j'ai un peu feuilleté et un élément du préambule a attiré mon attention :
En outre, j'ai pu lire sur un autre topic de ce forum ce qui suit :
Ces deux points de vue sont d'après moi en totale contradiction : Les auteurs du document donnent une vision assez physicienne des maths. Ils signifient que ce caractère ne se rencontre pas seulement en maths, mais aussi dans le reste des sciences expérimentales ou non, et ce en passant par les sciences de l'esprit, le raisonnement, et la pensée philo.
Passer du particulier au général, n'est-ce pas le propre de la physique ? N'est-ce pas une science qui s'appuie sur des observations de la nature pour en déduire des principes muables, qui peuvent être remaniés et invalidés au cours du temps ?
Justement, j'avais vu un documentaire sur la physique du début du XXème siècle, qui traitait de la volonté des physiciens de réunifier les grandes théories en une théorie du tout. N'est-ce pas une preuve de ce passage nécessaire du particulier au général ?
Les maths, elles, s'appuient sur des principes fondamentaux, les axiomes. Ceux-ci sont posés comme piliers incontestables, base de tout raisonnement sous-jacent.
Comment peut-on dire que les maths sont une science "du particulier au général", alors que l'on construit chaque démonstration autour d'un nombre fini de principes immuables ?
"En cheminant avec Kakeya", p.2 a écrit:... Confronté à de telles questions, le mathématicien n'a souvent d'autre choix que de s'intéresser à des cas particuliers ou des questions annexes plus accessibles. Ce questions particulières, qui peuvent paraître bien anecdotiques, offrent parfois, l'Histoire l'a montré, des lumières décisives sur les questions les plus générales. Ce passage du particulier au général n'est pas propre aux mathématiques et se rencontre dans tous les savoirs...
En outre, j'ai pu lire sur un autre topic de ce forum ce qui suit :
Domi Lefebvre - Issu de "L'enseignement des maths par l'exemple" - Maths forum a écrit:D'ailleurs, en parlant de physique, j'ai depuis longtemps constaté, et je ne suis ni le premier ni le seul, qu'il existe une différence fondamentale entre l'enseignement des maths et de la physique. Dans la plupart des cas (dans l'enseignement supérieur et en fin de secondaire et pour les écoles que je connais): en math on part du général vers le particulier - l'exemple - alors qu'en physique on part presque toujours du particulier - une manip - pour aller au général - la loi qui gouverne le phénomène. Les quelques profs de physique qui essayent de partir d'une loi générale pour descendre vers les applications se plantent à tous les coups...
Ces deux points de vue sont d'après moi en totale contradiction : Les auteurs du document donnent une vision assez physicienne des maths. Ils signifient que ce caractère ne se rencontre pas seulement en maths, mais aussi dans le reste des sciences expérimentales ou non, et ce en passant par les sciences de l'esprit, le raisonnement, et la pensée philo.
Passer du particulier au général, n'est-ce pas le propre de la physique ? N'est-ce pas une science qui s'appuie sur des observations de la nature pour en déduire des principes muables, qui peuvent être remaniés et invalidés au cours du temps ?
Justement, j'avais vu un documentaire sur la physique du début du XXème siècle, qui traitait de la volonté des physiciens de réunifier les grandes théories en une théorie du tout. N'est-ce pas une preuve de ce passage nécessaire du particulier au général ?
Les maths, elles, s'appuient sur des principes fondamentaux, les axiomes. Ceux-ci sont posés comme piliers incontestables, base de tout raisonnement sous-jacent.
Comment peut-on dire que les maths sont une science "du particulier au général", alors que l'on construit chaque démonstration autour d'un nombre fini de principes immuables ?
Nightmare a écrit:Un tour des mathématiques pour un tour d'aiguille : [url="http://math.univ-lyon1.fr/~borrelli/Kakeya/En_cheminant_avec_Kakeya.pdf"]En cheminant avec Kakeya[/url]
Conseillé à tous.
:happy3:
Résume-le nous en quelques mots de ton cru, toi qui l'as lu et avoues priser l'échange courant direct...
Salut, Kikoo ; je vais tâcher de te répondre, du peu d'expérience que j'ai :
- D'abord, pour moi les maths ne sont pas une science à proprement parler, mais une sorte de construction de l'esprit, une sorte de truc imaginaire, qui n'a pas de réalité, mais bref on s'en fout c'est pas la question.
- Je pense que ce que DominiqueLefebvre voulait dire n'est pas vraiment ce qu'il a écrit. Il a raison dans le sens où en physique un "chapitre" s'ouvre par une expérience et continue avec la théorie qu'il y a derrière. Je ne suis pas scientifique, mais c'est la démarche naturelle je pense qui guide la science, on observe, on expérimente et ensuite on modélise. Par la suite on peut tirer sur le modèle et proposer des expériences qui vont le mettre en défaut et donc reconstruire un modèle plus large, ou mieux abouti.
Exemple. La loi des gazs parfait ; un jour, un grand sage (ou fou ? ) a calculer le produit PV et a dit qu'il était constant. Bref, il pond PV=nRT , amen, puis 100 plus tard (ou pas) des expériences mettent le modèle en défaut, Van Der Waals propose le modèle .. [dont je ne me souviens plus -> Google ].
Donc on observe que en physique :
On part du Particulier, l'expérience [PV=Cste pour 8 gazs] , puis on généralise (PV=nRT pour tout les gazs), et on continue de généraliser [VdW].
Par ailleurs, moi qui a beaucoup critiqué la physique de lycée, je trouve que cette façon de procéder est assez "historique" et c'est mieux comme cela, d'ailleurs soit dit en passant, n'importe quel prof de physique que j'ai eu, donnait des documents sur les Physiciens les avancées etc. Alors qu'en maths, pas une seule fois, et je trouve cela presque choquant, peut-tu immaginer un cours sur Voltaire (mettons Candide comme Oeuvre), sans que le prof te parle de qui était Voltaire et à quelle époque il a vécu ?? Non ? Et bien c'est comme faire un cours sur la dérivation sans parler de Newton ou Leibniz.
- En maths, c'est pareil je trouve, les avancées sont toujours du particulier au général, est-ce que ça t'arrive de faire un cours sur les Plynômes de degrés quelconques et que deux ans plus tard le prof dise : Pfff les équations algébriques de degré 5 c'est tellement simple avec une calculette 4 opérations que maintenant on se concentre sur les polynômes de degré 1 [j'ai évité 0 quand même (ou même - l'infini)]
Non bien sûr ! C'est possible que tu approfondisse un domaine, ce qui est normal, mais on fait pas de saut en arrière. Dans la manière d'aborder un problème c'est pareil .
Exemple. Calculer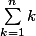 . Personne (qui aurait cherché a résoudre le problème) ne dirait : Vu mon attirail d'outils superpuissants du tac au tac ça fait
. Personne (qui aurait cherché a résoudre le problème) ne dirait : Vu mon attirail d'outils superpuissants du tac au tac ça fait }{2}) et tu remarquera que pour n=4 la somme fait 10.
et tu remarquera que pour n=4 la somme fait 10.
C'est le parfait genre de problème où lorsque tu essaye tu peut conjecturer le résultat et le prouver par récurrence. Pas besoin d'être génial. D'ailleurs, j'ai essayé de faire calculer cette somme sur papier à un copain qui n'aime pas les maths (des notes pitoyables en TS hélas) et il n'a rien su faire, même pas tester pour n=1,2 ou 3. Plus tard, quand on faisait du Rami (jeu de cartes) où on a souvent des cartes, où on doit savoir compter vite et bien ses points, il m'a étonné, il abat :
2,3,4,5,6,7,8 d'un côté et 7,8,9,10 ; il me dit, j'ai les points (il faut au moins 51 pts) je peut descendre. Je lui ai demandé "comment tu sais que tu as assez", il m'a dit qu'après deux ans a jouer on sait compter vite, et en lui demandant sa méthode il m'explique :
* S'il y a un nombre impair de cartes, comme 2,3,4,5,6,7,8, on prend la carte centrale et on multiplie par le nombre de cartes : 2+3+4+5+6+7+8=5*7 et s'il y a un nombre pair de cartes on additionne les extremales :
7+8+9+10=(7+10)+(8+9)=17+17 ...
Bref, en faisant des cas particuliers, avec des dessins (enfin des cartes pour le coup, mais c'est un support comme un autre) il en a déduit une manière générale d'agir. Et ça c'est des maths pour moi.
En général c'est assez prétentieux de vouloir résoudre un problème sans s'investir dans les cas particulier (quoi, moi me réduire à n=2, mais je suis en maths sup t'es fou ^^ , sauf que quand le prof de maths t'explique que lui il est mathématiquement faible et qu'il teste n=2 et que comme par hasard la généralisation tombe avec, ça fait réfléchir). Donc la démarche de résolution est souvent celle ci :
Test sur des cas particuliers, dessins, reformulations, liens avec des énoncés connus, réduction des hypothèses (f est continue dans l'énoncé, mais j'ai envie de dériver, pas de soucis je rajoute f dérivable (même C1) et je continue d'avancer, tant pis il vaut mieux savoir faire un peu que rien, et puis ça donne souvent des idées), donc oui les maths c'est jamais du général au particulier.
Par contre ce que Dominique voulait dire c'est que les maths au lycée, ne sont pas présentées pareil (ça doit quand même dépendre des profs), on insiste beaucoup moins sur l'aspect historique et les personnages, on insiste moins sur la recherche (utiliser sa tête ie devoir faire des tests sur des cas particuliers etc..) et ça décourage plein de monde (et je l'avoue, faire des maths lycée c'est un peu morne et si je n'aimais pas les maths je les haïrais), donc les chapitres sont souvent faits que on regarde toute la théorie (des polynômes par exemple) et que ensuite on s'intéresse dans les exercices, a plusieurs choses qui ont motivées en réalité la théorie précédente. Maintenant les profs font plus d'activités d'introduction que avant (mais perso ma prof de TS ne le faisait que très peu).
Exemple. Quand on fait la dérivation, parfois dans les exercices on trouve de la "physique" où en fait on refait le chemin de Newton ...
Maintenant, je sais pas quel niveau tu as, mais si tu as ton brevet je te propose cet exercice pour voir si tu as compris (si tu ne connais pas les notations, demande je te donnerais tout ce qui te faut) :
On note l'indicatrice d'euler et
l'indicatrice d'euler et  un entier naturel. Calculer
un entier naturel. Calculer 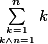
Maintenant je répond à Nightmare : Ce livre est écrit par l'ancien prof de TS d'un de mes camarade de cette année. J'ai commencé à le lire et il est très très bien ; te connaissant un peu, je pense que tu as dû l'apprécier !
- D'abord, pour moi les maths ne sont pas une science à proprement parler, mais une sorte de construction de l'esprit, une sorte de truc imaginaire, qui n'a pas de réalité, mais bref on s'en fout c'est pas la question.
- Je pense que ce que DominiqueLefebvre voulait dire n'est pas vraiment ce qu'il a écrit. Il a raison dans le sens où en physique un "chapitre" s'ouvre par une expérience et continue avec la théorie qu'il y a derrière. Je ne suis pas scientifique, mais c'est la démarche naturelle je pense qui guide la science, on observe, on expérimente et ensuite on modélise. Par la suite on peut tirer sur le modèle et proposer des expériences qui vont le mettre en défaut et donc reconstruire un modèle plus large, ou mieux abouti.
Exemple. La loi des gazs parfait ; un jour, un grand sage (ou fou ? ) a calculer le produit PV et a dit qu'il était constant. Bref, il pond PV=nRT , amen, puis 100 plus tard (ou pas) des expériences mettent le modèle en défaut, Van Der Waals propose le modèle .. [dont je ne me souviens plus -> Google ].
Donc on observe que en physique :
On part du Particulier, l'expérience [PV=Cste pour 8 gazs] , puis on généralise (PV=nRT pour tout les gazs), et on continue de généraliser [VdW].
Par ailleurs, moi qui a beaucoup critiqué la physique de lycée, je trouve que cette façon de procéder est assez "historique" et c'est mieux comme cela, d'ailleurs soit dit en passant, n'importe quel prof de physique que j'ai eu, donnait des documents sur les Physiciens les avancées etc. Alors qu'en maths, pas une seule fois, et je trouve cela presque choquant, peut-tu immaginer un cours sur Voltaire (mettons Candide comme Oeuvre), sans que le prof te parle de qui était Voltaire et à quelle époque il a vécu ?? Non ? Et bien c'est comme faire un cours sur la dérivation sans parler de Newton ou Leibniz.
- En maths, c'est pareil je trouve, les avancées sont toujours du particulier au général, est-ce que ça t'arrive de faire un cours sur les Plynômes de degrés quelconques et que deux ans plus tard le prof dise : Pfff les équations algébriques de degré 5 c'est tellement simple avec une calculette 4 opérations que maintenant on se concentre sur les polynômes de degré 1 [j'ai évité 0 quand même (ou même - l'infini)]
Non bien sûr ! C'est possible que tu approfondisse un domaine, ce qui est normal, mais on fait pas de saut en arrière. Dans la manière d'aborder un problème c'est pareil .
Exemple. Calculer
C'est le parfait genre de problème où lorsque tu essaye tu peut conjecturer le résultat et le prouver par récurrence. Pas besoin d'être génial. D'ailleurs, j'ai essayé de faire calculer cette somme sur papier à un copain qui n'aime pas les maths (des notes pitoyables en TS hélas) et il n'a rien su faire, même pas tester pour n=1,2 ou 3. Plus tard, quand on faisait du Rami (jeu de cartes) où on a souvent des cartes, où on doit savoir compter vite et bien ses points, il m'a étonné, il abat :
2,3,4,5,6,7,8 d'un côté et 7,8,9,10 ; il me dit, j'ai les points (il faut au moins 51 pts) je peut descendre. Je lui ai demandé "comment tu sais que tu as assez", il m'a dit qu'après deux ans a jouer on sait compter vite, et en lui demandant sa méthode il m'explique :
* S'il y a un nombre impair de cartes, comme 2,3,4,5,6,7,8, on prend la carte centrale et on multiplie par le nombre de cartes : 2+3+4+5+6+7+8=5*7 et s'il y a un nombre pair de cartes on additionne les extremales :
7+8+9+10=(7+10)+(8+9)=17+17 ...
Bref, en faisant des cas particuliers, avec des dessins (enfin des cartes pour le coup, mais c'est un support comme un autre) il en a déduit une manière générale d'agir. Et ça c'est des maths pour moi.
En général c'est assez prétentieux de vouloir résoudre un problème sans s'investir dans les cas particulier (quoi, moi me réduire à n=2, mais je suis en maths sup t'es fou ^^ , sauf que quand le prof de maths t'explique que lui il est mathématiquement faible et qu'il teste n=2 et que comme par hasard la généralisation tombe avec, ça fait réfléchir). Donc la démarche de résolution est souvent celle ci :
Test sur des cas particuliers, dessins, reformulations, liens avec des énoncés connus, réduction des hypothèses (f est continue dans l'énoncé, mais j'ai envie de dériver, pas de soucis je rajoute f dérivable (même C1) et je continue d'avancer, tant pis il vaut mieux savoir faire un peu que rien, et puis ça donne souvent des idées), donc oui les maths c'est jamais du général au particulier.
Par contre ce que Dominique voulait dire c'est que les maths au lycée, ne sont pas présentées pareil (ça doit quand même dépendre des profs), on insiste beaucoup moins sur l'aspect historique et les personnages, on insiste moins sur la recherche (utiliser sa tête ie devoir faire des tests sur des cas particuliers etc..) et ça décourage plein de monde (et je l'avoue, faire des maths lycée c'est un peu morne et si je n'aimais pas les maths je les haïrais), donc les chapitres sont souvent faits que on regarde toute la théorie (des polynômes par exemple) et que ensuite on s'intéresse dans les exercices, a plusieurs choses qui ont motivées en réalité la théorie précédente. Maintenant les profs font plus d'activités d'introduction que avant (mais perso ma prof de TS ne le faisait que très peu).
Exemple. Quand on fait la dérivation, parfois dans les exercices on trouve de la "physique" où en fait on refait le chemin de Newton ...
Maintenant, je sais pas quel niveau tu as, mais si tu as ton brevet je te propose cet exercice pour voir si tu as compris (si tu ne connais pas les notations, demande je te donnerais tout ce qui te faut) :
On note
Maintenant je répond à Nightmare : Ce livre est écrit par l'ancien prof de TS d'un de mes camarade de cette année. J'ai commencé à le lire et il est très très bien ; te connaissant un peu, je pense que tu as dû l'apprécier !
Mickael :
Je comprends très bien ce que tu me dis à propos de la physique : Ce principe de raisonnement qui part du particulier au général n'est pas qu'une manière de réfléchir, c'est le fondement de la physique et c'est son caractère même. Je peux de même en juger par la façon qu'ont les physiciens de construire une démonstration ou bien celle de mener un calcul en physique : les simplifications de modèle, l'usage de DL, ... pourraient faire vomir des matheux plus rigoureux.
Idem en ce qui concerne l'enseignement de ces matières durant mon secondaire : mon prof de physique de 1ère et Tale nous mettait des points historiques dans les fascicules qu'il écrivait. Cela nous permettait de remettre en contexte la façon qu'avaient les physiciens de résoudre un problème.
En maths, le cours se déroulait toujours du début à la fin avec un même motif :
I)... 1) Définition 1.1 Théorème; 1.2 ...
II)... 1) Définitions, ...
...
Je ne sais pas si cette démarche est propre aux spécificités de chaque matière ou à l'usage pédago.
Tu me parles des maths académiques. Je veux plutôt voir comment se sont mises en place les mathématiques au cours du temps : Est-on constamment passé du particulier au général ou du général au particulier ?
On constate que les Egyptiens et les Grecs de l'antiquité (je fais écho au défi posé ) ont posé les bases de la géométrie Euclidienne et de l'arithmétique.
) ont posé les bases de la géométrie Euclidienne et de l'arithmétique.
Sans construire rigoureusement N, ils l'ont quand même découvert et utilisé. Puis on avance dans la frise chrono : On étend les propriétés de N à Z, on découvre les rationnels, décimaux, réels, et on avance en sophistication.
N'est-ce pas étendre le général vers le particulier ?
Etc : A chaque étape, on se base sur ce qui a été fait précédemment pour le perfectionner. Mais là je me pose une question : Peut-on réellement parler de général et de particulier en maths ? :hum:
(voilà je m'embrouille, chuis comme ça ^^)
Pour passer à l'exo que tu m'as proposé, voilà ce que j'ai à dire.
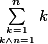 , cela s'interprète comme la somme des entiers premiers avec n, et qui lui sont inférieurs, n donné.
, cela s'interprète comme la somme des entiers premiers avec n, et qui lui sont inférieurs, n donné.
Nous avons phi l'indicatrice d'Euler, qui est le cardinal de l'ensemble des entiers premiers avec n.
Sachant que je ne connais pas de "truc" algébrique afin de calculer une telle somme, je vais essayer de conjecturer une formule à partir d'essais.
Je prendrai successivement n=9; n=10 et n=13 donc, arbitrairement
Soit n=9, les entiers premiers avec 9 et qui lui sont inférieurs sont 1; 2; 4; 5; 7; 8
Leur somme vaut 23
Soit n=10, les entiers premiers avec 10, plus petits que 10, sont 1; 3; 6; 7; 9
Leur somme vaut 26
Soit n=13, les entiers premiers avec 13 sont 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12 (basiquement tous les entiers inférieurs à 13 vu que 13 est premier)
Leur somme vaut 12(13)/2=6*13=78
phi(9)=6
phi(10)=5
phi(13)=12
Et là, grosse réflexion de malade... qui avorte ^^
Je comprends très bien ce que tu me dis à propos de la physique : Ce principe de raisonnement qui part du particulier au général n'est pas qu'une manière de réfléchir, c'est le fondement de la physique et c'est son caractère même. Je peux de même en juger par la façon qu'ont les physiciens de construire une démonstration ou bien celle de mener un calcul en physique : les simplifications de modèle, l'usage de DL, ... pourraient faire vomir des matheux plus rigoureux.
Idem en ce qui concerne l'enseignement de ces matières durant mon secondaire : mon prof de physique de 1ère et Tale nous mettait des points historiques dans les fascicules qu'il écrivait. Cela nous permettait de remettre en contexte la façon qu'avaient les physiciens de résoudre un problème.
En maths, le cours se déroulait toujours du début à la fin avec un même motif :
I)... 1) Définition 1.1 Théorème; 1.2 ...
II)... 1) Définitions, ...
...
Je ne sais pas si cette démarche est propre aux spécificités de chaque matière ou à l'usage pédago.
Tu me parles des maths académiques. Je veux plutôt voir comment se sont mises en place les mathématiques au cours du temps : Est-on constamment passé du particulier au général ou du général au particulier ?
On constate que les Egyptiens et les Grecs de l'antiquité (je fais écho au défi posé
Sans construire rigoureusement N, ils l'ont quand même découvert et utilisé. Puis on avance dans la frise chrono : On étend les propriétés de N à Z, on découvre les rationnels, décimaux, réels, et on avance en sophistication.
N'est-ce pas étendre le général vers le particulier ?
Etc : A chaque étape, on se base sur ce qui a été fait précédemment pour le perfectionner. Mais là je me pose une question : Peut-on réellement parler de général et de particulier en maths ? :hum:
(voilà je m'embrouille, chuis comme ça ^^)
Pour passer à l'exo que tu m'as proposé, voilà ce que j'ai à dire.
Nous avons phi l'indicatrice d'Euler, qui est le cardinal de l'ensemble des entiers premiers avec n.
Sachant que je ne connais pas de "truc" algébrique afin de calculer une telle somme, je vais essayer de conjecturer une formule à partir d'essais.
Je prendrai successivement n=9; n=10 et n=13 donc, arbitrairement
Soit n=9, les entiers premiers avec 9 et qui lui sont inférieurs sont 1; 2; 4; 5; 7; 8
Leur somme vaut 23
Soit n=10, les entiers premiers avec 10, plus petits que 10, sont 1; 3; 6; 7; 9
Leur somme vaut 26
Soit n=13, les entiers premiers avec 13 sont 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12 (basiquement tous les entiers inférieurs à 13 vu que 13 est premier)
Leur somme vaut 12(13)/2=6*13=78
phi(9)=6
phi(10)=5
phi(13)=12
Et là, grosse réflexion de malade... qui avorte ^^
[quote="Kikoo Essaye de voir comment on peut le démontrer. Utilise les armes que tu as.
Sinon, regarde ce qui suit :
La somme s'arrête a n-1 de toute façon , par exemple pour n=9 :
1 2 3 4 5 6 7 8
Pour n=13 c'est premier, tu as bien vu que tout marche (jusqua 12 obv)
Pour n=10 :
1 2 3 4 5 6 7 8 9
Question : Que remarque tu sur les nombres en gras ? Sont-ils répartis aléatoirement ?
Peut-on les regrouper ?
D'ailleurs peut-tu avant, calculer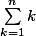 par la méthode que j'ai donnée dans le post précédent (celle du Rami bien sûr ^^ )
par la méthode que j'ai donnée dans le post précédent (celle du Rami bien sûr ^^ )
Sinon, regarde ce qui suit :
La somme s'arrête a n-1 de toute façon , par exemple pour n=9 :
1 2 3 4 5 6 7 8
Pour n=13 c'est premier, tu as bien vu que tout marche (jusqua 12 obv)
Pour n=10 :
1 2 3 4 5 6 7 8 9
Question : Que remarque tu sur les nombres en gras ? Sont-ils répartis aléatoirement ?
Peut-on les regrouper ?
D'ailleurs peut-tu avant, calculer
Je suis allé me doucher et mon père en a profité pour prendre l'ordi, je suis sur mon mobile...
J'arrive pas trop à identifier une forme, même avec l'indication que tu m'as donné (diviser la somme par phi).
La cause doit être un manque de sommeil, j'espère ^^
Je reprendrai tout ça demain, et merci pour tout Mickael :)
J'arrive pas trop à identifier une forme, même avec l'indication que tu m'as donné (diviser la somme par phi).
La cause doit être un manque de sommeil, j'espère ^^
Je reprendrai tout ça demain, et merci pour tout Mickael :)
Moi aussi je suis sur mobile.
Ce n'est pas grave si tu n'arrive pas a conjecturer. Regarde la deuxième partie des indications, essaie de voir. Mais tu peut aussi aller dormir, en général ça fit du bien. Demain je serais la par intermitance sur mobile uniquement et que le soir car je travaille la journee et suis pas la le soir. Mais si tu poste je répondrais.
Ce n'est pas grave si tu n'arrive pas a conjecturer. Regarde la deuxième partie des indications, essaie de voir. Mais tu peut aussi aller dormir, en général ça fit du bien. Demain je serais la par intermitance sur mobile uniquement et que le soir car je travaille la journee et suis pas la le soir. Mais si tu poste je répondrais.
Pour la méthode Rami :
On constate que si l'on dispose d'un nombre impair de cartes, en progression arithmétique, nous avons le modèle suivant que l'on prend en exemple :
n-2; n-1; n; n+1; n+2
La valeur médiane est n. On fait la somme qui vaut n*5+1+2-1-2=n*5
Ton copain sait intuitivement que ce que l'on rajoute à la valeur médiane et ce que l'on lui soustrait s'annule parfaitement.
Si le nombre de cartes est pair, nous prenons le modèle suivant :
n-3; n-2; n-1; n; n+1; n+2
Par symétrie, il sait que la somme de deux nombres de part et d'autre du "miroir" est toujours la même. C'est le raisonnement du petit Gauss : donner deux séries de nombres S et S (n nombres à sommer pour S) qu'il range de façon symétrique afin d'obtenir n termes qui valent n+1 après addition.
Il multiplie donc : 2S=n(n+1) et divise par 2 : S=n(n+1)/2
On constate que si l'on dispose d'un nombre impair de cartes, en progression arithmétique, nous avons le modèle suivant que l'on prend en exemple :
n-2; n-1; n; n+1; n+2
La valeur médiane est n. On fait la somme qui vaut n*5+1+2-1-2=n*5
Ton copain sait intuitivement que ce que l'on rajoute à la valeur médiane et ce que l'on lui soustrait s'annule parfaitement.
Si le nombre de cartes est pair, nous prenons le modèle suivant :
n-3; n-2; n-1; n; n+1; n+2
Par symétrie, il sait que la somme de deux nombres de part et d'autre du "miroir" est toujours la même. C'est le raisonnement du petit Gauss : donner deux séries de nombres S et S (n nombres à sommer pour S) qu'il range de façon symétrique afin d'obtenir n termes qui valent n+1 après addition.
Il multiplie donc : 2S=n(n+1) et divise par 2 : S=n(n+1)/2
Triplette, désolé ^^
Benekire : T'as souligné les entiers premiers de telle sorte que je puisse voir une symétrie !
1 2 3 4 5 6 7 8 (9)
Et si l'on donne 8=9-1; 7=9-2; 5=9-4; 4=9-5; 2=9-7; 1=9-8; cela donne S=1+2+4+5+7+8=9*6-(1+2+4+5+7+8)
Si on donne 6=phi(9), nous avons le résultat suivant : 2S=9*phi(9) d'où S=9*phi(9)/2
Mais j'attends de voir comment généraliser !!
Benekire : T'as souligné les entiers premiers de telle sorte que je puisse voir une symétrie !
1 2 3 4 5 6 7 8 (9)
Et si l'on donne 8=9-1; 7=9-2; 5=9-4; 4=9-5; 2=9-7; 1=9-8; cela donne S=1+2+4+5+7+8=9*6-(1+2+4+5+7+8)
Si on donne 6=phi(9), nous avons le résultat suivant : 2S=9*phi(9) d'où S=9*phi(9)/2
Mais j'attends de voir comment généraliser !!
Kikoo <3 Bieber a écrit:Triplette, désolé ^^
Benekire : T'as souligné les entiers premiers de telle sorte que je puisse voir une symétrie !
1 2 3 4 5 6 7 8 (9)
Et si l'on donne 8=9-1; 7=9-2; 5=9-4; 4=9-5; 2=9-7; 1=9-8; cela donne S=1+2+4+5+7+8=9*6-(1+2+4+5+7+8)
Si on donne 6=phi(9), nous avons le résultat suivant : 2S=9*phi(9) d'où S=9*phi(9)/2
Mais j'attends de voir comment généraliser !!
Oui bonne conjecture !!
J'ai mis en gras, pour que tu vois la symétrie. 8=9-1 ; 7=9-2 etc ...
Tu as tout ce qui faut pour conclure très simplement, tout fonctionne comme pour n=9. Au fait désolé hier soir j'ai pas vérifié tes calculs, je voulais dormir ^^
En fait, ce qui m'a sans doute gêné, c'est de considérer cette somme comme étant une somme algébrique : Sommer les n tel que k est premier avec n et k plus petit que n, c'est pour moi sommer sur les k. Peut-être que je me focalise trop sur les variables indicées ! J'espère que tu vois ce que je veux dire :)
Oulà, j'ai plus les rélfexes en arithmétique ! Va falloir que je développe tout ça par écrit ^^
Pour démontrer que le pgcd de a et b est le même que a et c, il faut montrer que l'ensemble des diviseurs communs de a et c est le même que celui de a et b...
Oulà, j'ai plus les rélfexes en arithmétique ! Va falloir que je développe tout ça par écrit ^^
Pour démontrer que le pgcd de a et b est le même que a et c, il faut montrer que l'ensemble des diviseurs communs de a et c est le même que celui de a et b...
Kikoo <3 Bieber a écrit:En fait, ce qui m'a sans doute gêné, c'est de considérer cette somme comme étant une somme algébrique : Sommer les n tel que k est premier avec n et k plus petit que n, c'est pour moi sommer sur les k. Peut-être que je me focalise trop sur les variables indicées ! J'espère que tu vois ce que je veux dire
En fait,
Kikoo <3 Bieber a écrit:Oulà, j'ai plus les rélfexes en arithmétique ! Va falloir que je développe tout ça par écrit ^^
Pour démontrer que le pgcd de a et b est le même que a et c, il faut montrer que l'ensemble des diviseurs communs de a et c est le même que celui de a et b...
Oui c'est très simple :
En effet, si a divise k et n-k alors il divise leur somme, donc ...
réciproquement, si b divise k et n alors il divise leur différence : n-k donc ...
60 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
