Tiroirs et t-shirts

[lol37]

Salut,
quel est le nombre de façon de ranger t-shirts dans tiroirs ?
Je crois que c'est mais je ne suis pas sur
Merci d'avance !

[arnaud32]

combien de t-shirt tu peux mettre par tiroire?

[beagle]

si on prend des exemples simples, ta formule ne marche pas.
1 tee shirt 3 tiroirs
7 tee shirt 1 tiroir

[lol37]

autant qu'on veux. il n'y a pas de limites ( les t shirts sont de taille S et les tiroirs sont vraiment très grand )

[arnaud32]

et tous les t-shirt sont identifiables??

[lol37]

ils sont de couleurs blanches, donc identiques

[arnaud32]

s'ils sont tous differents, c'est n^p
pour chaque tshirt tu donnes le numero du tiroire tu as n choix a chaque fois

s'ils sont identiques tu dois diviser par le nombre de permutations soit p!

d'ou

[lol37]

si tu prends on a 3 combinaisons possibles alors que ta formule en donne 2...

deux t shirts dans la première 1 dans l'un et dans l'autre et 2 dans la deuxième : 3.

[arnaud32]

tu as raison c'est plus complique que ce que je pensais. :hein:
je penses qu'il va falloir distinguer le cas p>n de n=

[arnaud32]

si tu notes ce nombre tu as
mais ca me parait assez complique

[arnaud32]

avec des conditions aux limites et

[arnaud32]

c'est quoi l'enonce excate de ton exercice?

[lol37]

c'est le même que j'ai donné à mon premier post, les t shirts ne sont pas distinguables( on ne prend pas en compte l'ordre ), et il n'y a pas de limite de place dans les tiroirs.

[benekire2]

Salut, je n'ai pas tout lu :/

Je me souviens d'un exo : De combien de facons peut-on ranger n Tshirts dans p tiroirs p
et il est facile d'adapter cela au problème en séparant les cas ..

[Ben314]

Salut,
- La solution n'est surement pas vu que cette quantité vaut 0 lorsque p>=n alors que, perso, je n'ai aucun problème pour ranger mes 5-Tshirts dans un seul tiroir.
- La solution n'est surement pas vu que, par exemple pour n=1 et p=2 cela ne fait pas un nombre entier.

En supposant que les tiroirs sont "identifiables" (le premier tiroir, le second tiroir,...) mais pas les Tshirts, le problème se résume à trouver le nombre de n-uplets d'entiers positifs ou nuls tels que ( est le nombre de Tshirts dans le tiroir k).
C'est un "archi clasique" du dénombrement : à une solution on "associe" une suite de "cases" blanches/noires de la façon suivante :
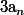
On met cases blanches puis une case noire puis cases blanches puis une case noire puis cases blanches .... puis une case noire puis cases blanches.
On se retrouve ainsi avec p+n-1 cases dont n-1 sont noires. Il est clair que, réciproquement, toute suite de p+n-1 cases dont n-1 sont noires donne une solution .
Le nombre de solutions est donc

[arnaud32]

tres joli! je ne conaissais pas ce "super classique", ou je ne m'en souvenais pas :-)