Principe des tiroirs

par **t.itou29** » 04 Déc 2013, 19:14

Bonsoir,
J'ai quelques difficultés avec cet exercice :

Soit r+1 nombres possédant ensemble r diviseurs premiers distincts. Montrer que l'ensemble de ces nombres contient un sous-ensemble dont le produit est un carré.

J'ai pensé pour les tiroirs à des r-uplet où à chacun des exposant des diviseurs premiers d'un nombre est associé sa parité, si deux nombres (ou produit de plusieurs nombres) appartiennent au même tiroir alors leur produit est un carré. Il y a alors

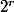
tiroirs. Mais pour les objets je sais pas trop comment les dénombrer. J'aurais besoin d'un peu d'aide.
EDIt: j'ai peut-être trouvé il y a

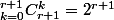
produits et la conclusion se déduit facilement. Est-ce correct ?

par **nodjim** » 04 Déc 2013, 20:11

Un nombre possède toujours au moins 2 diviseurs: 1 et lui même, dont un seul diviseur premier au minimum. Si les r+1 nb donnent ensemble r diviseurs premiers, alors que chacun en produit au moins 1, c'est que au moins 2 sont identiques. Le produit de ces 2 là est un carré.

par **t.itou29** » 04 Déc 2013, 20:16

nodjim a écrit:Un nombre possède toujours au moins 2 diviseurs: 1 et lui même, dont un seul diviseur premier au minimum. Si les r+1 nb donnent ensemble r diviseurs premiers, alors que chacun en produit au moins 1, c'est que au moins 2 sont identiques. Le produit de ces 2 là est un carré.

Cela signifie que les deux ont un facteur premier en commun mais pas que leur produit donne un carré ? Ça dépend de leurs autres facteurs, par exemple pour 2,6,5,75 il faut prendre 3 nombres, 2x6x75=900, 2 nombres ne suffit pas.

par **nodjim** » 04 Déc 2013, 20:20

Prends 4 nombres. S'ils fournissent ensemble 3 diviseurs premiers distincts seulement, alors que j'ai expliqué qu'ils en fournissaient 4 au minimum (distincts ou non), c'est que 2 d'entre eux sont égaux.
p1,p2,p3,p4: 4 diviseurs. Si seulement 3 distincts, c'est que 2 d'entre eux sont identiques.
Compris ?

par **t.itou29** » 04 Déc 2013, 20:27

nodjim a écrit:Prends 4 nombres. S'ils fournissent ensemble 3 diviseurs premiers distincts seulement, alors que j'ai expliqué qu'ils en fournissaient 4 au minimum (distincts ou non), c'est que 2 d'entre eux sont égaux.
p1,p2,p3,p4: 4 diviseurs. Si seulement 3 distincts, c'est que 2 d'entre eux sont identiques.
Compris ?

Désolé mais je vois toujours pas, quelque chose m'échappe, si je prend 22;6;3;33 leurs diviseurs premiers sont 11;3;2 mais il y en pas deux d'egaux (enfin si mais confondus mais ça change rien)

par **Tiruxa** » 05 Déc 2013, 11:06

Bonjour,

J'ai essayé de comprendre votre problème.
Prenons le cas où r=2 ce sera plus simple pour commencer
et intéressons nous aux exposants ou plutôt à leur parité
On notera 1 si l'exposant est impair et 0 s'il est pair

Donc on a 4 catégories de nombres
(1,1), (1,0), (0,1), (0,0)
Les nombres de types (0,0) sont bien sûr des carrés

Donc prenons les r+1 nombres (ici 3 nombres)
Si l'un est de type (0,0) c'est bon.
S'il y en a deux du même type leur produit est de type (0,0) donc carré
S'ils sont tous les trois de types différents le produit des 3 est de type 00 donc carré
en effet (1,1) + (1,0) + (0,1) = (0,0) (on ajoute modulo 2)

Donc dans tous les cas on a bien un sous ensemble dont le produit est un carré.

Voilà, hélas j'ai du mal à généraliser...

par **t.itou29** » 05 Déc 2013, 17:16

Tiruxa a écrit:Bonjour,

J'ai essayé de comprendre votre problème.
Prenons le cas où r=2 ce sera plus simple pour commencer
et intéressons nous aux exposants ou plutôt à leur parité
On notera 1 si l'exposant est impair et 0 s'il est pair

Donc on a 4 catégories de nombres
(1,1), (1,0), (0,1), (0,0)
Les nombres de types (0,0) sont bien sûr des carrés

Donc prenons les r+1 nombres (ici 3 nombres)
Si l'un est de type (0,0) c'est bon.
S'il y en a deux du même type leur produit est de type (0,0) donc carré
S'ils sont tous les trois de types différents le produit des 3 est de type 00 donc carré
en effet (1,1) + (1,0) + (0,1) = (0,0) (on ajoute modulo 2)

Donc dans tous les cas on a bien un sous ensemble dont le produit est un carré.

Voilà, hélas j'ai du mal à généraliser...

Finalement je crois avoir trouvé :
Il y a

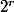
r-uplets possibles avec r diviseurs. Or il y a

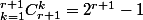
produits possibles avec r+1 nombres, par le principe des tiroirs au moins 2 produits sont donc associés au même r-uplet.
Mais votre piste en ajoutant modulo 2 a l'air plus simple mais je ne vois pas comment la généraliser.

par **nodjim** » 05 Déc 2013, 18:52

J'ai mal lu l'énoncé. Je vais y réfléchir.

par **nodjim** » 05 Déc 2013, 19:40

Voila comment je vois les choses:
On écrit chaque nombre avec r chiffres, chaque chiffre représentant la parité de puissance de chaque nombre premier ordonné, donc on écrit un nombre binaire.
Le nombre de combis qu'on peut faire avec les r+1 nombres est de 2^(r+1)-1, -1 car on ne peut pas écrire le produit 0, c'est à dire la combi d'aucun nombre.
mais, avec un nombre binaire de r chiffres, on ne peut établir que 2^r nombres binaires différents, donc moins que les 2^(r+1)-1 qu'on a écrit. Donc il y a forcément des nombres binaires identiques. Associer 2 de ces nombres identiques (ajouter les puissances) conduit obligatoirement à un carré.
NB: ce nombre binaire "000.." apparaitra de toute façon dans la liste puisqu'on aura fait toutes les combis possibles, dont l'association de 2 nombres identiques, encore fallait il prouver qu'il devait apparaitre.

CQFD

par **t.itou29** » 05 Déc 2013, 20:48

nodjim a écrit:Voila comment je vois les choses:
On écrit chaque nombre avec r chiffres, chaque chiffre représentant la parité de puissance de chaque nombre premier ordonné, donc on écrit un nombre binaire.
Le nombre de combis qu'on peut faire avec les r+1 nombres est de 2^(r+1)-1, -1 car on ne peut pas écrire le produit 0, c'est à dire la combi d'aucun nombre.
mais, avec un nombre binaire de r chiffres, on ne peut établir que 2^r nombres binaires différents, donc moins que les 2^(r+1)-1 qu'on a écrit. Donc il y a forcément des nombres binaires identiques. Associer 2 de ces nombres identiques (ajouter les puissances) conduit obligatoirement à un carré.
NB: ce nombre binaire "000.." apparaitra de toute façon dans la liste puisqu'on aura fait toutes les combis possibles, dont l'association de 2 nombres identiques, encore fallait il prouver qu'il devait apparaitre.

CQFD

Merci, j'ai réussi à trouver le pdf de corrigés et c'est en substance la preuve donnée.

par **Tiruxa** » 05 Déc 2013, 23:36

Je comprends votre raisonnement, mais je rajouterai une précision.

Pour reprendre le même vocabulaire, on est sûr (th des tiroirs) qu'il y a deux combinaisons donnant le même nombre binaire.
Ensuite on les multiplie ces nombres.
Il se peut que l'une soit la combi n1*n2*n3 et l'autre la combi n2*n4
Le produit donnera clairement 00..... mais ce sera n1*n2²*n3*n4 ce qui est génant car faisant apparaître deux fois le facteur n2
Mais n2² est aussi du type 00.... donc n1*n3*n4 est également de type 00.....
Autrement dit en regroupant on doit éliminer les doublons.
Cela vous a sans doute paru évident mais c'est ce qui me bloquait...

par **Ben314** » 06 Déc 2013, 01:20

nodjim a écrit:Le nombre de combis qu'on peut faire avec les r+1 nombres est de 2^(r+1)-1, -1 car on ne peut pas écrire le produit 0, c'est à dire la combi d'aucun nombre.

Juste une remarque : on peut parfaitement compter 2^(r+1) combinaisons.
Il suffit de dire (convention classique) que le produit de rien du tout fait 1.
Aprés, le tiroir dans lequel va être situé le 1, c'est le tiroir où tout les exposants des nombres premiers sont pairs (vu que pour 1 tout les exposants sont égaux à 0).
Si ce tiroir là contient un deuxième nombre, ben ça voudra directement dire que ce nombre est un carré et... c'est ce qu'on veut obtenir...

par **Tiruxa** » 06 Déc 2013, 09:44

Il me semble qu'il y a un problème dans cette phrase :

Ben314 a écrit:Si ce tiroir là contient un deuxième nombre, ben ça voudra directement dire que ce nombre est un carré et... c'est ce qu'on veut obtenir...

Le principe des tiroirs n'assure pas que ce tiroir contienne deux combinaisons mais qu'au moins un tiroir (sans savoir lequel) contienne au moins deux combinaisons.

par **nodjim** » 06 Déc 2013, 18:03

En fait, je ne suis qu'à moitié satisfait de ma démo.
J'aurais dû le présenter comme ça:
On écrit tjs les nombres comme un binaire de r chiffres. Au moins l'un des chiffres est 1, sinon, c'est un carré (on exclut 0).
Essayons l'arithmétique sous cette forme bizarre.
A+0=A ça c'est assez évident, de même A+A=0000..
Soit 2 nombres distincts A et B.
A+B=S et c'est assez facile de montrer que S<>A et S<>B.
Commençons la liste des combis possibles
A
B
A+B
on ajoute un 3ème nombre C. Ce 3ème nombre va engendrer 4 nouveaux nombres dans la liste:
C
C+A
C+B
C+A+B
etc..
Soit au total, si r nombres, 2^r -1 nombres. Or avec r chiffres, si on exclut le 0, on peut bien exactement s'arranger pour avoir que des nombres distincts.
Comme le problème exige un nombre supplémentaire, celui ci sera forcément égal à l'un des nombres de la liste établie. Or on a vu que la somme de 2 nombres égaux valait 000.., c'est à dire un carré, et ce nombre supplémentaire va bien engendrer la somme avec son alter ego.

Je trouve ça assez difficile pour des Lycéens.

par **Ben314** » 06 Déc 2013, 18:32

Tiruxa a écrit:Il me semble qu'il y a un problème dans cette phrase

non non...

Ben314 a écrit:Si ce tiroir là contient un deuxième nombre, ben ça voudra directement dire que ce nombre est un carré et... c'est ce qu'on veut obtenir...

par **t.itou29** » 07 Déc 2013, 07:59

nodjim a écrit:En fait, je ne suis qu'à moitié satisfait de ma démo.
J'aurais dû le présenter comme ça:
On écrit tjs les nombres comme un binaire de r chiffres. Au moins l'un des chiffres est 1, sinon, c'est un carré (on exclut 0).
Essayons l'arithmétique sous cette forme bizarre.
A+0=A ça c'est assez évident, de même A+A=0000..
Soit 2 nombres distincts A et B.
A+B=S et c'est assez facile de montrer que SA et SB.
Commençons la liste des combis possibles
A
B
A+B
on ajoute un 3ème nombre C. Ce 3ème nombre va engendrer 4 nouveaux nombres dans la liste:
C
C+A
C+B
C+A+B
etc..
Soit au total, si r nombres, 2^r -1 nombres. Or avec r chiffres, si on exclut le 0, on peut bien exactement s'arranger pour avoir que des nombres distincts.
Comme le problème exige un nombre supplémentaire, celui ci sera forcément égal à l'un des nombres de la liste établie. Or on a vu que la somme de 2 nombres égaux valait 000.., c'est à dire un carré, et ce nombre supplémentaire va bien engendrer la somme avec son alter ego.

Je trouve ça assez difficile pour des Lycéens.

Pourtant votre première démo était celle donnée par le corrigé.
J'avais l'attention de d'utiliser cet exemple pour un exposé de maths en anglais sur le principe de tiroirs mais je crois que c'est un peu trop compliqué, je vais rester sur les exemplez classiques.

par **nodjim** » 07 Déc 2013, 10:14

Non seulement ma 1ère démo n'était pas au point, mais la seconde comporte encore un trou.
Si j'ai dans ma liste 2^k-1 nombres différents, et que j'ajoute un n, on peut très bien avoir:
n+s1=s2, avec s1 et s2 déja dans la liste.
Mais si s1 et s2 ont des termes communs, on peut réécrire l'équation
n+s1'=s2' , s1' et s2' étant 2 autres nombres de la liste débarassés des termes communs à s1 et s2.
Mais dans ce cas, il existe aussi dans la liste s1'+s2', car ils n'ont pas de termes communs. Et on va alors, avec n, créer le nombre n+s1'+s2'=s2'+s2'=2s2'=0=carré.

par **nodjim** » 07 Déc 2013, 10:53

Cela dit, le msg du 5/12 17h16 est correct et bien plus court.

Principe des tiroirs

principe des tiroirs

Qui est en ligne