[TERMINÉ] si l'intersection de mZ avec nZ égal mnZ, alors pg
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lp.vitor
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Nov 2012, 14:47
-
 par lp.vitor » 27 Nov 2012, 14:53
par lp.vitor » 27 Nov 2012, 14:53
Je voudrais bien montrer que
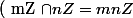 \Rightarrow pgcd (m, n) = 1$)
Quelque idée?
Merci bcp.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Nov 2012, 14:57
par leon1789 » 27 Nov 2012, 14:57
soit d un diviseur commun à m et n
que dire du nombre
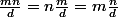
?
-
lp.vitor
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Nov 2012, 14:47
-
 par lp.vitor » 27 Nov 2012, 15:08
par lp.vitor » 27 Nov 2012, 15:08
c'est le ppcm (m, n), mais, comment je peux l'utiliser pour montrer que d = 1?
Merci
-
lp.vitor
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Nov 2012, 14:47
-
 par lp.vitor » 27 Nov 2012, 15:09
par lp.vitor » 27 Nov 2012, 15:09
oh, pardon, j'ai pense que tu avais dit "d = pgcd (m, n)"

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Nov 2012, 15:10
par leon1789 » 27 Nov 2012, 15:10
tu peux penser à d = pgcd(m, n) si tu veux.
Ma question :
que dire de l'entier
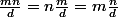
?
Ce nombre est multiple de ... et de ..., donc multiple de ... , donc d = 1.
Regarde ton énoncé pour répondre à ma question.
-
lp.vitor
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Nov 2012, 14:47
-
 par lp.vitor » 27 Nov 2012, 15:14
par lp.vitor » 27 Nov 2012, 15:14
je vais voir.
Merci
-
lp.vitor
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Nov 2012, 14:47
-
 par lp.vitor » 27 Nov 2012, 15:21
par lp.vitor » 27 Nov 2012, 15:21
quand-même, je ne vois pas comment je peux utiliser que

est partinent à

pour montrer que d = 1
?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Nov 2012, 15:32
par leon1789 » 27 Nov 2012, 15:32
Tu es d'accord que

est appartinent à

?
Et quelle est ton hypothèse sur

dans l'exo ?
-
lp.vitor
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Nov 2012, 14:47
-
 par lp.vitor » 27 Nov 2012, 15:35
par lp.vitor » 27 Nov 2012, 15:35
oh, c'est vrai.
Comment j'ai perdu tant des temps avec ça?
Merci bcp!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités