Groupes abéliens

[Imod]

Bonsoir à tous :we:

Des sujets récents m'ont rappelé quelques problèmes de groupes pas vraiment faciles .

1°) Si dans un groupe G les carrés commutent entre eux et les cubes commutent aussi entre eux alors G est abélien ( généralisation ? ) .
2°) Si est un homomorphisme injectif ou surjectif d’un groupe G alors G est abélien .
3°) Si et sont des homomorphismes d’un groupe G alors G est abélien ( généralisation ?)

Bon courage :zen:

Imod

[ffpower]

Pour dire que le sujet ne s est pas paumé,chui en train d y reflechir(mais c pas facile).Mais t aurai mieux fait de poster dans enigmes,la ca va se perdre en moins de 2..

[ThSQ]

De la gymnastique de groupe !


Un essai pour le 2) dans le cas où le morphisme est surjectif :

donc en simplifiant
et en simplifiant :
Comme le morphisme est surjectif les commutent avec tout le monde et d'où il découle 'stochement que G est abélien.


C'est très amusant, on remplit des pages de calculs abscons :marteau: !

[ThSQ]

Et dans le cas où il est injectif, en réutilisant les propriétés trouvées au-dessus :

[ffpower]

J ai le cas injectif(je crois)
donc .En réélevant au carré, on obtient donc donc par injectivité

Edit:mais euuuh

[ThSQ]

Edit:mais euuuh

:bad3:

Je retourne bosser l'info après cet épisode récré, je te laisse les autres cas :ptdr: :lol4:

[ffpower]

pour le 3
on a cette fois et ( donc donc .Donc les carrés commutent,or on a deja vu que les cubes commutent donc on peut utiliser 1(qui a l air d etre la question la plus chaude)

[Imod]

Bon , on ne parle plus du 2°) reste le 1°) et le 3°) :we:

La généralisation du 1°) ne pose pas de problème et peut même s'attaquer d'emblée celle du 3°) est carrément bestiale :arf: Dans tout les cas il faut prévoir "quelques" feuilles de brouillon .

Imod

[Imod]

D'accord pour la réduction du 3°) au 1°) :++:

Imod

[ThSQ]

"quelques" feuilles de brouillon .

:++:

C'est le même genre d'astuces qui le fait ?

[Imod]

C'est le même genre d'astuces qui le fait ?

Il y a plusieurs solutions ( toutes astucieuses ) , une que j'aime particulière ment utilise les sous-groupes engendrés par les carrés et par les cubes .

Imod

[ffpower]

Je suis a 2 doigts..J ai montré que G quotienté par son centre était commutatif...Je torche ca avt minuit^^

[Imod]

Prends ton temps :we:

Je laisse encore un peu le sujet sur ce forum et je bascule le reste dans la section énigme car les généralisations méritent un peu d'attention :zen:

Imod

[ffpower]

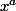
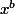
Bon,voila ma demo(j en ai bavé :mur: ).Je l ai généralisais au passage car ca change rien en fait(comme tu disais^^).Donc je suppose qu on a 2 entiers a et b premiers entre eux tels que pour tout x,y, et commutent, et et commutent.Je veux donc montrer que G est commutatif.Deja,je fixe une bonne fois pour toutes u et v tel que au+bv=1 vu que j en aurais besoin plusieurs fois.Ensuite quelques notations:

-Z=centre de G=ss groupe des éléments qui commutent avec tout
-D=groupe dérivé de G=ss groupe engendré par les commutateurs
-H=ss groupe engendré par les
-K=ss groupe engendré par les

tites remarques préliminaires:H et K sont commutatifs par hypothese.De plus le groupe engendré par H et K,c est G tout entier(car ) donc:
-pour montrer que G est commutatif,il suffit de montrer que tout élément de H commute avec tout élément de K
- puisque si ,x commute avec tout élément de H et tout élément de K

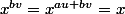
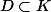
Regardons maintenant le groupe quotient G/H.Pour tout x de G/H,on a .En particulier on a donc .Or pour tout x,y de G/H, et commutent donc x et y commutent.Ainsi G/H est commutatif donc .De la meme maniere, .Au final,


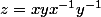
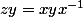
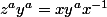
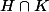
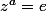
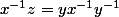
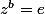
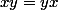
Maintenant soit x dans H et y dans K.Posons .z est dans D,donc dans le centre Z.En élevant la relation a la puissance a,on obtient .Mais est dans donc dans Z,donc en simplifiant par on a .De la meme maniere,en utilisant on obtient ,donc finalement et ,G est donc commutatif

Voila,ya plus qu a réfléchir sur la généralisation de 3) :zen:

[Imod]

C'est bon :++: , j'aurais juste précisé que H et K sont des sous-groupes normaux de G ce qui est évident car les conjugués des puissances a sont des puissances a .

Pour la généralisation du 3°) je te laisse chercher un peu ( ce n'est pas facile :doh: ) sinon je donnerais des indices .

Imod

[ffpower]

car c était censé etre facile ca ...sigh :euh:

[SimonB]

car c était censé etre facile ca ...sigh :euh:

Oui, mais c'est essentiel pour passer au quotient :we:

SimonB, qui n'avait rien trouvé de tout ça, mais qui continue à plancher sur le dernier !

[Imod]

car c était censé etre facile ca ...sigh :euh:

Disons que déjà le critère n'est pas facile à trouver , par exemple on peut trouver un groupe non commutatif dans lequel et sont des morphismes mais pas et :doh:

Imod

[ffpower]

Autre généralisation a méditer:que dire si pour tout x,y de G,il existe a et b premier entre eux tels que x^a et y^a commutent,x^b et y^b commutent :we:

[ffpower]

Oui, mais c'est essentiel pour passer au quotient :we:

SimonB, qui n'avait rien trouvé de tout ça, mais qui continue à plancher sur le dernier !

Je ne parlais du quotient,je m etonnais juste que imod considérais le 1) comme facile(ce qui veut donc dire que pour la généralisation du 3),ca va envoyé^^

Au fait Imod,ta dit qu il y avait plusieurs demo pour 1).Est ce que la mienne en faisait partie?Et est ce que tu peux en donner une autre,pour voir une autre maniere d aborder le truc?