Somme d'une série
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
teamprepa
- Membre Naturel
- Messages: 58
- Enregistré le: 25 Aoû 2015, 16:29
-
 par teamprepa » 26 Déc 2015, 22:31
par teamprepa » 26 Déc 2015, 22:31
Bonjour, je dois trouver la somme de la série de terme général :
 * 1/2^n)
. Je sais déjà que la série converge car j'ai pu la majorer par la série géométrique


Pour trouver la somme je bloque parce que j'ai du n dans le cosinus et je ne vois pas comment faire..
((x appartenant à R et N un entier naturel))
Merci d'avance pour vos indications
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 26 Déc 2015, 22:40
par MouLou » 26 Déc 2015, 22:40
Salut.
=Re(e^{inx})=Re(e^{ix}^{n}))
. Donc
}{2^{n}}=Re((\frac{e^{ix}}{2})^{n}))
-
teamprepa
- Membre Naturel
- Messages: 58
- Enregistré le: 25 Aoû 2015, 16:29
-
 par teamprepa » 26 Déc 2015, 23:02
par teamprepa » 26 Déc 2015, 23:02
MouLou a écrit:Salut.
=Re(e^{inx})=Re(e^{ix}^{n}))
. Donc
}{2^{n}}=Re((\frac{e^{ix}}{2})^{n}))
Merci pour ta réponse mais je vois pas comment ça m'aide à trouver la somme...
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 26 Déc 2015, 23:15
par MouLou » 26 Déc 2015, 23:15
Serie géométrique?
-
teamprepa
- Membre Naturel
- Messages: 58
- Enregistré le: 25 Aoû 2015, 16:29
-
 par teamprepa » 27 Déc 2015, 01:28
par teamprepa » 27 Déc 2015, 01:28
MouLou a écrit:Serie géométrique?
qu'est ce qui me dit que
/2|<1)
?

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 27 Déc 2015, 01:42
par Sake » 27 Déc 2015, 01:42
teamprepa a écrit:qu'est ce qui me dit que
/2|<1)
?
Ben |e^(ix)| = 1 pour tout x...
-
teamprepa
- Membre Naturel
- Messages: 58
- Enregistré le: 25 Aoû 2015, 16:29
-
 par teamprepa » 27 Déc 2015, 02:22
par teamprepa » 27 Déc 2015, 02:22
Sake a écrit:Ben |e^(ix)| = 1 pour tout x...
ok merci bcp
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 27 Déc 2015, 23:44
par MouLou » 27 Déc 2015, 23:44
Ton courage à autant manipuler le langage Tex sur ce forum force le respect!
Pour moi c'est juste ce que tu as écrit
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 28 Déc 2015, 00:16
par aymanemaysae » 28 Déc 2015, 00:16
Merci M. Moulou: j'ai appris à rédiger avec Latex sur ce forum. Vous et les autres, vous avez beaucoup fait pour moi, et je ne saurai guère vous remercier.
-
teamprepa
- Membre Naturel
- Messages: 58
- Enregistré le: 25 Aoû 2015, 16:29
-
 par teamprepa » 01 Jan 2016, 15:15
par teamprepa » 01 Jan 2016, 15:15
La formule pour une somme géométrique de raison r c'est 1-r^(n+1)/1-r ?
Parce que M.aymanemaysae semble avoir fait le contraire..
-
Robot
 par Robot » 01 Jan 2016, 15:21
par Robot » 01 Jan 2016, 15:21
teamprepa a écrit:La formule pour une somme géométrique de raison r c'est 1-r^(n+1)/1-r ?
Parce que M.aymanemaysae semble avoir fait le contraire..
Qu'appelles-tu "contraire" ???
-
teamprepa
- Membre Naturel
- Messages: 58
- Enregistré le: 25 Aoû 2015, 16:29
-
 par teamprepa » 01 Jan 2016, 15:24
par teamprepa » 01 Jan 2016, 15:24
Robot a écrit:Qu'appelles-tu "contraire" ???
L'opposé.
Pour moi la formule c'est 1-r^(n+1)/1-r
Pourtant lui il a utilisé r^(n+1)-1/r-1
-
Robot
 par Robot » 01 Jan 2016, 15:25
par Robot » 01 Jan 2016, 15:25
teamprepa a écrit:L'opposé.
Pour moi la formule c'est 1-r^(n+1)/1-r
Pourtant lui il a utilisé r^(n+1)-1/r-1
Donc pour toi,
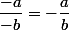
???
-
teamprepa
- Membre Naturel
- Messages: 58
- Enregistré le: 25 Aoû 2015, 16:29
-
 par teamprepa » 01 Jan 2016, 15:32
par teamprepa » 01 Jan 2016, 15:32
Robot a écrit:Donc pour toi,
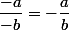
???
ah oui je fais n'importe quoi ce matin..
Je me trompe peut être vu mon degré de fatigue mais lorsqu'il développe et qu'il obtient celle ligne
x) cos(x) - 2 cos((n+1)x) - 2^{n+1} (cos(x) - 2) + sin((n+1)x) sin(x)}{2^n(5 - 4 cos(x))})
+ Im(

)
c'est pas plutot sin^2((n+1)x) qu'on devrait avoir?
-
Robot
 par Robot » 01 Jan 2016, 15:34
par Robot » 01 Jan 2016, 15:34
teamprepa a écrit:vu mon degré de fatigue
Vu tes interventions dans ce fil et dans l'autre, une petite sieste s'impose.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités