Dynamique 2

Rebonjour, deuxième exercice qui me pose problème.


Voilà l'énoncé :
On suspend un point matériel M, de massem, à un fil inextensible de longueur 1 et de masse négligeable, qui est fixé en un point O1 d'un axe vertical Oz. Le point M est animé d'un mouvement circulaire uniforme de vitesse angulaire w constante dans le plan xOy. Le fil O1M reste incliné du même angle ALPHA par rapport à l'axe Oz.

Déterminer l'angle d'inclinaison constant ALPHA du pendule avec l'axe Oz en fonction de w, 1 et du champ de pesanteur.




Ici encore, je ne vois pas du tout par où commencer. Ou plutôt comment y parvenir.

Merci de votre aide.

Mister Red a écrit:Rebonjour, deuxième exercice qui me pose problème.


Voilà l'énoncé :
On suspend un point matériel M, de massem, à un fil inextensible de longueur 1 et de masse négligeable, qui est fixé en un point O1 d'un axe vertical Oz. Le point M est animé d'un mouvement circulaire uniforme de vitesse angulaire w constante dans le plan xOy. Le fil O1M reste incliné du même angle ALPHA par rapport à l'axe Oz.

Déterminer l'angle d'inclinaison constant ALPHA du pendule avec l'axe Oz en fonction de w, 1 et du champ de pesanteur.




Ici encore, je ne vois pas du tout par où commencer. Ou plutôt comment y parvenir.

Merci de votre aide.

Dans un référentiel lié à M :

Les 2 forces agissant sur le point matériel sont :
Son poids P = ... (norme, direction et sens)
La force centrifuge due à la rotation : Fc = ... (norme, direction et sens)

La résultante de ces 2 forces est dans la direction du fil et donc ...

:zen:

La force centrifuge ? Qu'est-ce que ?

Moi j'aurai plutôt dis que les forces agissant sur M était son poids P et la tension du fil.

Quand tu tournes sur un cercle, il y a une force centripète. Si tu te places dans le référentiel du point M, il a l'impression de se faire tirer vers dehors. C'est simplement la grandeur de la force centripète [mw^2/r] dans le sens opposé. Dès lors, pour un alpha constant, tu sais quelle force tu dois annuler (Qu'est-ce qui ferait se balancer un pendule ?)

A+

Le problème c'est que l'on a pas encore vu cette force centripète, je ne vois même pas de quoi il s'agit en fait. N'aurais-tu pas une autre façon de faire stp ?

Merci quand même pour le tuyau !

Non. Si tu ne connais pas la force centripète, tu n'as aucune autre force à relier avec w. Il te faut l'équilibre des forces dans la direction orthogonale au fil. Si il y a une force dans cette direction, ton pendule se balance. Si la somme des forces dans cette direction est nulle, il ne bouge pas, et par conséquent reste à un angle constant.

Je ne comprends pas puisqu'on n'a pas vu la force centripète.

En fait moi je tombe sur ça :

On prend la base de projection polaire en M, vecteur Ur dans le sens du fil, Ualpha orthogonal à Ur.

D'après le PFD on a :
m x vecteur A = vecteur P + vecteur T

or vecteur OM = longueur du fil x vecteur Ur = vecteur Ur
d'où vecteur v = alphapoint x vecteur Ualpha
alpha=constant => alphapoint=0 => vecteur v = 0 => vecteur a =0


sur /vecteur Ur : -m x longueur fil x (alphapoint)² = P x cos(alpha) - T
P x cos(alpha) - T = 0

sur /vecteur Ualpha : m x longueur fil x alphadeuxpoints = -P x sin(alpha)
-p x sin(alpha) = 0

Or on sait que w² = g / l ici donc que w² = g


Voilà mes premières pistes en fait. Je ne sais par où continuer. Qu'en pensez-vous ?

Mister Red a écrit:Je ne comprends pas puisqu'on n'a pas vu la force centripète.

En fait moi je tombe sur ça :

On prend la base de projection polaire en M, vecteur Ur dans le sens du fil, Ualpha orthogonal à Ur.

D'après le PFD on a :
m x vecteur A = vecteur P + vecteur T

or vecteur OM = longueur du fil x vecteur Ur = vecteur Ur
d'où vecteur v = alphapoint x vecteur Ualpha
alpha=constant => alphapoint=0 => vecteur v = 0 => vecteur a =0


sur /vecteur Ur : -m x longueur fil x (alphapoint)² = P x cos(alpha) - T
P x cos(alpha) - T = 0

sur /vecteur Ualpha : m x longueur fil x alphadeuxpoints = -P x sin(alpha)
-p x sin(alpha) = 0

Or on sait que w² = g / l ici donc que w² = g


Voilà mes premières pistes en fait. Je ne sais par où continuer. Qu'en pensez-vous ?

Tu confonds w, rotation autour de l'axe de rotation, avec w, fréquence de balancement du pendule

Sans la force centrifuge/centripète, on ne s'en sort pas je pense Tu as besoin d'une force qui dépende de la vitesse de rotation autour de l'axe, sinon tu n'arrives à rien.

Donc à ce moment-là, trois forces entreraient en jeu : le poids, la tension de fil et la force centrifuge.

Ce que je n'ai pas compris, c'est que plus haut, tu dis "Si la somme des forces dans cette direction est nulle, il ne bouge pas, et par conséquent reste à un angle constant."
Mais l'angle est constant parce que la vitesse angulaire est constante. M peut bouge autour de l'axe Oz mais avec un angle constant.

Bonjour,

On peut parfaitement se passer de la force centrifuge. Tout dépend du référentiel de travail. Il y a 2 forces réelles qui s'applique sur le solide. Son poids et la tension du fil, c'est tout !

Si on se place dans un référentiel galiléen, on peut appliquer la deuxième loi de Newton, et m*a=P+T, avec a qui s'exprime dans le référentiel galiéen.

Si on travaille dans un référentiel non galiléen, comme le référentiel lié à la masse lors de sa rotation (il n'est pas galiléen car un référentiel est galiléen si et seulement si il est animé d'un mouvement rectiligne uniforme par rapport à un autre référentiel galiléen, ce qui n'est pas la cas ici), la deuxième loi de Newton ne s'applique plus.
On peut cependant montrer qu'en ajoutant des forces fictives dans le bilan des forces, on peut écrire la loi de Newton dans le nouveau référentiel. Soit m*a=P+T+Force_fictive, avec a qui s'exprime dans le référentiel liée à la masse m (et qui vaut 0 ici vu que la masse est immobile dans ce référentiel). La force fictive dans le problème qui nous occupe sera la force centrifuge.

Ainsi donc, pour résoudre ce problème sans la force centrifuge (ce qu'il faut faire car non vu en cours d'après ce qu'on nous dit), il suffit de travailler dans un référentiel galiléen, dans lequel la masse tourne autour de l'axe de z. On aura alors une accélération non nulle, qui est à l'origine de mouvement circulaire.

Black Jack a écrit:Dans un référentiel lié à M :

Les 2 forces agissant sur le point matériel sont :
Son poids P = ... (norme, direction et sens)
La force centrifuge due à la rotation : Fc = ... (norme, direction et sens)

La résultante de ces 2 forces est dans la direction du fil et donc ...

:zen:

Faux. Dans un référentiel lié à M, il faut rajouter la tension du fil, qui ne disparait pas et est toujours présente.
Dans un référentiel galiléen non lié à M, il y a deux forces : le poids et la tension du fil.

Oui merci beaucoup Benjamin, c'est ce que je me disais aussi...

Si je travaille dans le référentiel galiléen, voilà ce que j'obtiens :

On prend la base de projection polaire en M, vecteur Ur dans le sens du fil, Ualpha orthogonal à Ur.

D'après le PFD on a :
m x vecteur A = vecteur P + vecteur T

or vecteur OM = longueur du fil x vecteur Ur = vecteur Ur
d'où vecteur v = alphapoint x vecteur Ualpha
alpha=constant => alphapoint=0 => vecteur v = 0 => vecteur a =0


sur /vecteur Ur : -m x longueur fil x (alphapoint)² = P x cos(alpha) - T
P x cos(alpha) - T = 0

sur /vecteur Ualpha : m x longueur fil x alphadeuxpoints = -P x sin(alpha)
-p x sin(alpha) = 0

Après je ne sais pas où cela me conduit, je suis bloqué car contrairement a ce que tu dis, je trouve que l'accélération est nulle vu que la longueur du fil est constante non ?

La force centrifuge n'est pas fictive en soi. Quand la boule décrit un cercle, il y a une force centripète sur la boule par la corde, qui pousse la boule vers le centre. La force contraire est la force centrifgue sur la corde par la boule, par la 3ème loi de Newton. Maintenant, quand tu te places dans le référentiel de la boule, pour égaler le bilan des forces, tu dois dire que la force centripète agit sur la boule, ce que l'on sait erroné, car elle agit sur la corde. C'est pour cela que dans le référentiel de la boule, on dit que la force centrifuge est fictive, car tu t'intéresses vraiment aux force agissant sur la boule, et non sur la corde.

Le problème pour un référentiel galiléen est que la tension T est une combinaison de beaucoup d'éléments et donc difficile à exprimer par rapport à d'autres grandeurs. Je ne sais pas s'il est possible de faire sortir une force dépendant de w dans un système où tu considères que T et P. La tension dans le fil est la différence de la force centripète projetée sur la corde et de la gravité projetée sur la corde.

Dans ton cas j'ai l'impression que tu ne fais pas la différence entre la vitesse angulaire et l'angle alpha. La vitesse angulaire constante est dans le plan oxy, alors que l'angle alpha est dans le plan vertical. Donc l'angle alpha n'est psa constant seulement parce que w est constant. L'angle alpha est constant, car il n'y a pas d'accélération dans la direction U_alpha

Mathusalem a écrit:La force centrifuge n'est pas fictive en soi. Quand la boule décrit un cercle, il y a une force centripète sur la boule par la corde, qui pousse la boule vers le centre. La force contraire est la force centrifgue sur la corde par la boule, par la 3ème loi de Newton. Maintenant, quand tu te places dans le référentiel de la boule, pour égaler le bilan des forces, tu dois dire que la force centripète agit sur la boule, ce que l'on sait erroné, car elle agit sur la corde. C'est pour cela que dans le référentiel de la boule, on dit que la force centrifuge est fictive, car tu t'intéresses vraiment aux force agissant sur la boule, et non sur la corde.

Tu fais une grosse imprécision. Tu confonds force et accélération. La corde et la boule sont en contact physique. L'un donne une action sur l'autre et vice et versa. C'est la tension de la corde.
La boule est soumise à l'action physique de 2 forces, je maintiens. La gravité, et la tension de la corde.

Maintenant, quand on fait le PFD dans le référentiel galiléen, avec ces 2 forces (les seules), on trouve une accélération non nulle. Il se trouve que dans le cas de l'exo, cette accélération est constante dans le référentiel lié à la boule. On appelle cette accélération, l'accélération centripète.
Quand on change de référentiel, pour se placer dans celui lié à la boule, on exprime cette accélération centripète comme étant l'action d'une force. Cette force, tu as raison de le dire, respecte le principe d'action/réaction. Tu as donc une force centrifuge et centripète. Mais dans tous les cas, ce n'est là que l'expression de l'accélération centripète à laquelle est soumise la boule. Voilà pourquoi il s'agit d'une force fictive. C'est une accélération, qui est modélisé par une force quand on change de référentiel, pour pouvoir continuer à applique la deuxième loi de Newton.

Mathusalem a écrit:La force centrifuge n'est pas fictive en soi. Quand la boule décrit un cercle, il y a une force centripète sur la boule par la corde, qui pousse la boule vers le centre. La force contraire est la force centrifgue sur la corde par la boule, par la 3ème loi de Newton.

Sur ce point précis : La corde agit sur la boule par l'intermédiaire de la tension. Cette tension est dirigée dans l'axe du fil. Après, que la projection de la tension de la corde dans le plan Oxy soit en relation direct avec la valeur de la force centripète est une autre histoire. En aucun cas la tension de la corde est équivalente à la force centrifuge ou centripète.

Mister Red a écrit:Oui merci beaucoup Benjamin, c'est ce que je me disais aussi...

Si je travaille dans le référentiel galiléen, voilà ce que j'obtiens :

On prend la base de projection polaire en M, vecteur Ur dans le sens du fil, Ualpha orthogonal à Ur.

D'après le PFD on a :
m x vecteur A = vecteur P + vecteur T

or vecteur OM = longueur du fil x vecteur Ur = vecteur Ur
d'où vecteur v = alphapoint x vecteur Ualpha
alpha=constant => alphapoint=0 => vecteur v = 0 => vecteur a =0


sur /vecteur Ur : -m x longueur fil x (alphapoint)² = P x cos(alpha) - T
P x cos(alpha) - T = 0

sur /vecteur Ualpha : m x longueur fil x alphadeuxpoints = -P x sin(alpha)
-p x sin(alpha) = 0

Après je ne sais pas où cela me conduit, je suis bloqué car contrairement a ce que tu dis, je trouve que l'accélération est nulle vu que la longueur du fil est constante non ?

Je n'ai pas très bien compris ce que tu as dit.

Plaçons nous dans le référentiel galiléen fixe dont l'axe des z est confondu avec l'axe de rotation. Voir ce schéma
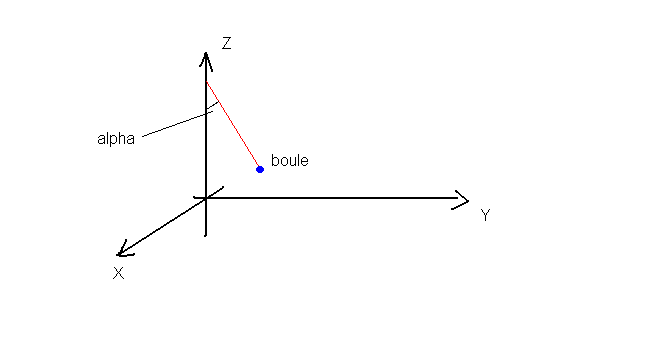
En vue de dessus, ça donne ça. Je définie ur et u_theta dans le plan Oxy

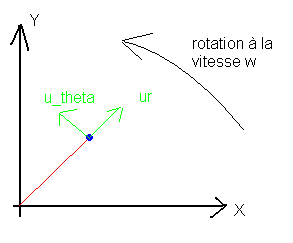
Exprime le poids en fonction de u_z. Exprime la tension de la corde en fonction de u_z et u_r.
Ecris le PFD dans Oxyz galiléen.
Projète le PFD sur u_z. Déduis-en la valeur de la tension de la corde.
Projète le PFD sur u_r. Déduis l'accélération à laquelle la masse m est soumise dans le référentiel galiléen. Cette accélération est l'accélération centripète.

Une fois que tu as ça, il faut calculer la valeur de cette accélération. Pour ca, il faut partir de l'équation du mouvement. Dans le plan Oxy, la boule suit une trajectoire circulaire uniforme. Donne la loi horaire x(t) et y(t) des coordonnées de la boule. Dérive deux fois pour trouver la valeur de l'accélération.

Tu pourras alors égaliser les 2 valeurs de l'accélération qu'on a trouvé. Il ne reste plus qu'à extraire l'angle alpha.

EDIT : plutôt que de passer par x(t) et y(t), tu peux directement écrire la vitesse v dans la base [u_r;u_theta;u_z], ça doit être dans ton cours je pense. Reste alors plus qu'à dériver cette vitesse pour avoir l'accélération.

Benjamin a écrit:Faux. Dans un référentiel lié à M, il faut rajouter la tension du fil, qui ne disparait pas et est toujours présente.
Dans un référentiel galiléen non lié à M, il y a deux forces : le poids et la tension du fil.

Pour être plus clair,

Dans un référentiel lié à la masse, la résultante du poids et de la force centrifuge est dans la direction du fil, ceci est suffisant pour pouvoir calculer l'angle que fait le fil avec la verticale. (en 1 ligne).

:zen:

J'ai donc recherché dans mon cours et j'ai trouvé :

vecteur v = R.Thétapoint.(vecteur Uthéta)
= Thétapoint.(vecteur Uthéta)

On trouve : vecteur a = Thétadeuxpoints.(vecteur Uthéta) - (Thétapoint)².(vecteur Ur)

Or Thétapoint=constante d'où Thétadeuxpoints=0

Donc vecteur a = - (Thétapoint)².(vecteur Ur)
Ici donc (vecteur a) c'est l'accélération centripète c'est ça ?

Après dois-je projetter toutes mes forces sur Ur ?

Mister Red a écrit:Donc vecteur a = - (Thétapoint)².(vecteur Ur)
Ici donc (vecteur a) c'est l'accélération centripète c'est ça ?

C'est exactement ça.

Tu as exprimé l'accélération d'une façon. Tu mets ce résultat de côté. Maintenant, exprime cette même accélération à partir du PFD, comme je l'ai expliqué.

Une fois que tu auras ces 2 résultats, tu pourras mettre les 2 ensembles.

Black Jack a écrit:Pour être plus clair,

Dans un référentiel lié à la masse, la résultante du poids et de la force centrifuge est dans la direction du fil, ceci est suffisant pour pouvoir calculer l'angle que fait le fil avec la verticale. (en 1 ligne).

:zen:

Tu as raison. Cependant, quand je vois la confusion qu'a Mathusalem entre force réelle, force fictive et accélération, je me dis qu'il n'est pas mauvais de partir de la base. Utiliser le PFD dans un référentiel non galiléen ne peut se faire qui si on a bien compris d'où vient la force centrifuge, et pourquoi il est nécessaire de rajouter ces forces fictives, comme dans le cas de la force de Coriolis par exemple.

En outre, Mister Red a été suffisamment clair sur son ignorance de la force centrifuge (les forces fictives ne sont en effet pas en programme au lycée en France). Il faut procéder par ordre. Avant de monter au sommet de la tour Eiffel, on passe par le premier étage. A faire les choses à l'envers, on peut arriver à la situation de Mathusalem qui ne sait pas qu'en réalité, la force centrifuge est une accélération et qui apparemment, ne sait pas résoudre ce problème sans utiliser cet artifice de calcul.

Je me rappelle mon excellent prof de physique de seconde qui m'avait dit : "On trouve de gens à BAC+2 qui ne savent pas repartir de la base, c'est bien dommage." La base, c'est le PFD dans Rgaliléen.

Mais je ne comprends pas, Théta est bien constant, donc Thétapoint doit être égal à 0, ce qui implique que la force centripète est nulle !! ?