Analyse

Bonjour à tous!
J'ai un exercice en analyse de Fourier, où je dois montrer que si est une fonction mesurable et additive, alors il existe M>0 tel que l'ensemble soit de mesure strictement positive.

En fait j'ai commencé par regarder pour voir si cet ensemble était de mesure strictement positive.
Mais je comprend pas comment expliquer que cet ensemble est de mesure strictement positive...

Je sais pas je dirais que

et donc y'a forcément un de mesure non nulle ( - additivité tout ça)

Oui c'est ce que j'ai écrit aussi. Mais je sais pas si c'est une bonne rédaction.

J'ai encore un problème! Décidément en ce moment, j'ai vraiment du mal avec l'analyse de fourier et l'algèbre!

Il faut que je montre maintenant que est un voisinage de 0 dans . Bon, alors déjà je sais que 0=0+0 appartient à . Maintenant je veux montrer que . Comme , j'essaye de montrer que .
Mais j'y arrive pas. Je sais pas si c'est la bonne méthode...

Bonjour,
c'est assez bizarre j'ai l'impression que l'hypothèse f additive ne sert à rien...

Bonjour Marie,
il y a quelque chose que je ne comprends pas, pourquoi dis tu que 0=0+0 est dans ? Aurait-ton ? Cela voudrait quand même dire que ...on aurait pas pris n'importe quel M alors...non ?

Comme f est additive par hypothèse on a forcement f(0)=0.
Parce que f(x+0)=f(x)+f(0)=f(x).

Au temps pour moi, j'avais fini par oublier cette hypothèse...

Je fais un petit up parce que je ne vois toujours pas comment montrer que est un voisinage de 0 dans .
Quelqu'un aurait-il une idée?
Merci d'avance

Un petit UP si quelqu'un sait faire....

Quelqu'un peut-il confirmer ou infirmer ceci :
Je réfléchis...pour plus de clarté je suppose n=1 et donc f:
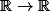
f est additive donc -linéaire. Si on se donne une base du espace vectoriel (possible par l'axiome du choix), f est alors entièrement déterminée par les images .
Je pose par exemple pour tout i sauf un nombre dénombrable d'entre eux : , f est alors automatiquement mesurable et vérifie les hypothèses de Marie49...
C'est le passage suivant où je ne suis pas si sur...:
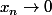
on peut choisir les de manière à ce que grâce à la densité de .
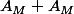
Si l'on pose alors alors f n'est pas bornée au voisinage de 0 or on veut montrer que est un voisinage de 0 et donc que f est bornée par 2M sur un voisinage de 0...
Je suis donc très tenté de dire que ce que demande Marie49 est faux...ou alors il manque une hypothèse du genre f continue en 0...

Salut tize!
Le but de l'exercice est justement de montrer que f est continue en 0. Donc ca ne fait malheureusement pas partie des hypothèses! :happy2:

Mais finalement je crois que j'ai fini par trouver. J'ai regardé le produit de convolution de , qui après calcul est égal à . Comme est continue, il existe un voisinage V de 0 sur lequel et comme , ca veut dire que et donc . Donc .

La question suivante, c'est montrer qu'il existe un voisinage de 0 sur lequel f est bornée. J'ai pris .

Et justement, après je dois montrer que f est continue en 0, puis sur . Et je n'arrive pas à montrer la continuité en 0. J'ai pris une suite telle que et je veux montrer que .
Il existe tel que dès que . Donc dès que . Mais on ne sait pas si M tend vers 0. Donc je suis coincée.

Ah je n'y avais pas pensé...mais un point me chiffonne : oui mais a-t-on car il me semble que le produit de convolution est continue si est de mesure finie.
Le fait que f soit additive implique-t-il que soit de mesure finie ?

P.S. c'est toi EtudianteAngers de FuturaScience ?

Non c'est pas moi mais j'ai vu aussi c'est la que j'ai trouvé l'idée!
Et je suis sûre que c une fille de ma classe parce que je suis d'angers aussi ! lol.
Justement je me demande aussi si la mesure est finie ou pas... Mais je suis sûre que c'est la bonne méthode parce que j'en vois pas d'autre.

Pour la fonction nulle ca marche pas , on a donc la mesure est pas finie.

marie49 a écrit:Pour la fonction nulle ca marche pas , on a donc la mesure est pas finie.

Oui mais la fonction nulle est continue en 0...

oui c'est vrai faudrait voir si dans le cas d'une fonction additive non nulle, est de mesure fiinie... Je vais regarder ca de plus près

Est-ce que mon raisonnement est juste ou pas?

Si , alors pour presque tout x.
Comme f est additive, on ne peut pas avoir de x tel que car sinon .
Donc, pour presque tout x.
Puis par récurrence, on ne peut pas avoir .....
Donc f est la fonction nulle presque partout.

marie49 a écrit:Est-ce que mon raisonnement est juste ou pas?
Si , alors pour presque tout x.

Dans l'ensemble je comprends le raisonnement sauf ça...pourquoi ?

marie49 a écrit:

Je sais pas, avec la définition ca me paraissait logique... Si la mesure de cet ensemble est infinie ca veut bien dire que x est dedans pour presque tout x? Non?