Morphisme de groupes

Je suis tombé sur un exercice sur le site de H. Gianella (http://mpsi3.llg.free.fr/), le resultat à démontrer me semble trop beau pour etre vrai, il me faut une démonstration! je rage de ne pas la trouver moi meme, mais bon je suis dessus...
Soit G, G deux groupes finis et f : G G un morphisme de groupes. Montrer que |G| = |Ker f| × |Im f|.

Salut,


Regarde la relation d'équivalence (prouver que ça en est une) :

x ~y ssi f(x) = f(y) ou de manière equivalente x ~y ssi f(x*y^-1) € Ker(f)

Salut !

est fini.
Bon, est un sous-groupe de .
Donc le théorème de Lagrange te dit que que est un diviseur de :
[CENTER][/CENTER]
pour un certain entier .
En fait, est l'indice de dans .
Alors, reste à trouver un iso entre et

merci bcp je v creuser

"N comme Nul", j'avais vu qqle chose com ca sur le net, mais le théoreme de Lagrange est je crois plus au programme (mais je me peu etre, pasque ca sera bizar qd meme) mais qu'est ce que le groupe G/Kerf?

Salut !

C'est le groupe quotient de par .

Je sais, ça n'avance pas à grand chose. Je peux un peu développer si tu veux.

oui stp, c'est nécessaire, un ensemble quotient avec une relation d'equivalence ok, mais le quotient d'un groupe par un de ses ss-groupes, j'avoue i am a bit lost

Le truc c'est que pour qu'un tel quotient soit muni d'une structure de groupe, il faut que le sous-groupe en question vérifie certaines conditions ... il doit être "normal".
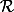Pour construire la chose, on part d'un sous-groupe de . On définit une relation d'équivalence définie par 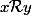ssi .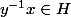
Mais pas de raison de privilégier l'ordre : on peut alors définir une autre relation d'équivalence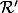 définie par : 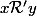ssi .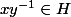
Si est commutatif (abélien), alors les deux relations coïncident.
Dans le cas général, si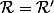 alors cela permet de munir le quotient 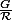d'une structure de groupe, on note alors 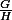ce groupe; est alors un sous-groupe normal (ou distingué, c'est comme on aime).

Au fait, tu connais les sous-groupes de ?

les sous groupe de Z,+ ? oui, nZ avec n un entier, non?

Oui !
Alors tu connais le groupe quotient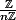
(l'ensemble des classes d'équivalences modulo )

La relation vue en Terminale :
ssi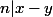
ne te rappelle alors rien ?

ssi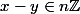

Le truc, c'est qu'ici, c'est la notation additive ... l'inverse est l'opposé.

Pour le cas de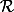 , les classes sont les 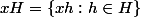et pour 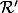les classes sont les .

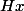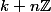Avec les classes sont et 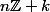, mais comme est abélien, tout coïncide.

Je sais, je suis fouillis.

Ha d'accord, je me disait que je comprenais pas la notation Z/nZ !! C'est juste un abus (de notation)... Je vois bien le parallèle entre G/Ker f et Z/Zn mais dans l'expression:



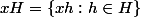
Qui est x? Pasque pour les classes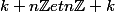 je vois qui est n et qui est k, mais là j'ai du louper qqlechose...

Sinon pour la relation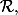 c'est une raltion entre quels ensembles? G dans G, H dans H? remarque ca ne peut pas etre de H dans H car alors pourt x,y de H, 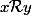... donc j'ai rien dit (a moins que ca soit une bétise)

Salut MooMooBloo !

"Qui est ?"
[INDENT] est un élément quelconque de
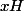est la classe (à gauche) de , modulo
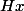( est la classe [à droite] de modulo )[/INDENT]

"Sinon pour la relation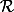 , c'est une raltion entre quels ensembles?"
[INDENT]Pas besoin de relations entre plusieurs ensembles, une relation binaire suffira :euh:
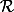est une relation (d'équivalence) sur
(la définir sur n'aurait aucun intérêt, puisqu'elle serait toujours vérifiée, eu égard au fait que 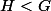)[/INDENT]

"pourt x,y de H, x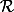y"
[INDENT](heureusement :lol5: !)[/INDENT]