Intégrale (2)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sl4cker
- Membre Naturel
- Messages: 21
- Enregistré le: 03 Déc 2006, 15:14
-
 par sl4cker » 03 Déc 2006, 15:48
par sl4cker » 03 Déc 2006, 15:48
Voici un autre exercice sur les intégrales Quelqu'un pourrait-il m'aider ???
1. Calculer Intégrale [( cos t / ( 2 + sin²t)) dt] de 0 a Pi
2. Donner une primitive sur R de la fonction f : t -> Racine carrée (t²+t+1)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 03 Déc 2006, 15:56
par tize » 03 Déc 2006, 15:56
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 03 Déc 2006, 16:42
par abcd22 » 03 Déc 2006, 16:42
Bonjour,
La deuxième est une intégrale abélienne, on écrit
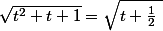^2 + \frac{3}{4} } = \frac{\sqrt{3}}{2}\sqrt{\(\frac{2t}{\sqrt{3}} +\frac{1}{\sqrt{3}} \)^2 + 1 })
puis on fait le changement de variable

puis u = sh v (car ch² x - sh² x = 1)(on peut aussi tout faire en un seul changement de variable).
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 03 Déc 2006, 16:46
par tize » 03 Déc 2006, 16:46
Bravo abcd22 :king2: je dois avouer que souvent ce genre d'intégrale me rebute et face à elle je me sens totalement impuissant...
-
sl4cker
- Membre Naturel
- Messages: 21
- Enregistré le: 03 Déc 2006, 15:14
-
 par sl4cker » 03 Déc 2006, 16:52
par sl4cker » 03 Déc 2006, 16:52
Merci pour la réponse mais je n'ai pas compris comment tu as fait. On demande une primitive et ... je n'ai pas compris
-
sl4cker
- Membre Naturel
- Messages: 21
- Enregistré le: 03 Déc 2006, 15:14
-
 par sl4cker » 03 Déc 2006, 16:55
par sl4cker » 03 Déc 2006, 16:55
et je ne comprends pas non plus à quoi correspond le v à la fin
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 03 Déc 2006, 17:44
par abcd22 » 03 Déc 2006, 17:44
tize a écrit:Bravo abcd22 :king2: je dois avouer que souvent ce genre d'intégrale me rebute et face à elle je me sens totalement impuissant...
J'ai la technique générale pour le calcul des intégrales abéliennes dans mes cours de prépa, une fois qu'on a compris la technique ce n'est pas très compliqué (sauf qu'il faut faire attention aux erreurs de calcul...).
Avec l'écriture que j'ai dite et le premier changement de variable, on obtient
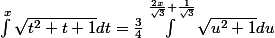
. Ensuite on refait un changement de variable u = sinh v (soit v = Argsh u) et du = cosh v dv :
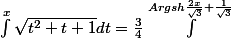}} \cosh^2{v} dv = \frac{3}{4} \int^{Argsh{\(\frac{2x}{\sqrt{3}} + \frac{1}{\sqrt{3}}\)}} \frac{1 + \cosh{(2v)}}{2} dv)
, après ça doit être finissable. Par contre j'ai pas très envie de redériver le résultat à la main pour vérifier si c'est ça...
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 03 Déc 2006, 17:48
par tize » 03 Déc 2006, 17:48
Ok, merci beaucoup !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 101 invités
