Integration des sin et cos
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pikacu
- Membre Naturel
- Messages: 25
- Enregistré le: 04 Nov 2006, 21:34
-
 par pikacu » 01 Déc 2006, 19:15
par pikacu » 01 Déc 2006, 19:15
Bonsoir!
j'ai un petit probleme pour le calcul de ce integrale:>>
integrale[cos(t)/(2+sin²t)]
est-ce que quelqun pourrait m'aider s'il vous plait?
Merci
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 01 Déc 2006, 19:32
par tize » 01 Déc 2006, 19:32
Bonjour,
tu as essayé le changement de variable
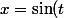)
?
-
pikacu
- Membre Naturel
- Messages: 25
- Enregistré le: 04 Nov 2006, 21:34
-
 par pikacu » 01 Déc 2006, 19:37
par pikacu » 01 Déc 2006, 19:37
oui, mais ça donne rien! :triste:
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 01 Déc 2006, 19:38
par tize » 01 Déc 2006, 19:38
Je crois que si ... 2 min je te poste ça .
-
pikacu
- Membre Naturel
- Messages: 25
- Enregistré le: 04 Nov 2006, 21:34
-
 par pikacu » 01 Déc 2006, 19:42
par pikacu » 01 Déc 2006, 19:42
ok merci beaucoup
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 01 Déc 2006, 19:48
par tize » 01 Déc 2006, 19:48
=x)
donc
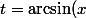)
et

}{2+\sin^2(t)}dt=\int\frac{\sqrt{1-\sin^2(t)}}{2+\sin^2(t)}=\int\frac{\sqrt{1-x^2}dx}{(2+x^2)\sqrt{1-x^2}}=\int\frac{dx}{2+x^2}=\frac{1}{2}\int\frac{dx}{1+\(\frac{x}{\sqrt{2}}\)^2}=\frac{1}{\sqrt{2}} \int\frac{du}{1+u^2}=\frac{1}{\sqrt{2}}\arctan(u))
avec un changement de variable

à la fin et en faisant attention aux bornes...
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
 par serge75 » 01 Déc 2006, 22:33
par serge75 » 01 Déc 2006, 22:33
encore plus simple : sin(t)=x, donc cos(t)dt=dx, et on obtient directemnt le réultat.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 92 invités
