Exo non résolu de première S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 03 Aoû 2006, 10:43
par nada-top » 03 Aoû 2006, 10:43
Hola.. :zen:
voilà je suis entrain de faire une révision au programme de prmière S avant de passer au terminal , alors j'essaye de faire quelques exos que j'ai pas encore résolu :marteau: voilà un exemple

je crois que vous allez voir plus d'exemples ces jours :ptdr: ) :
on considère l'application

définie par ceci :

:


 \rightarrow \frac{(x+y)(x+y+1)}{2} + x) [FONT=Comic Sans MS] démontrer que c'est une application bijective et déterminer
[FONT=Comic Sans MS] démontrer que c'est une application bijective et déterminer  [/FONT]
[/FONT] en fait je crois que j'ai démontré injectivité mais j'ai pas encore prouvé la surjectivité pour en déduire enfin la bijectivité :mur: ...si vous pouvez m'aider j'ai besoin seulement de qq indices :help:
PS : j'espère que ça sera clair pour une élève de première :hein: mais s'il y a d'autres méthodes de niveau terminal ou d'autre je suis prete à m'avancer :++:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 03 Aoû 2006, 10:58
par nada-top » 03 Aoû 2006, 10:58
Ah désolé je crois que c'est pas la bonne rubrique :marteau:il fallait plutot le poster a la rubrique LYCEE .. je me suis aperçue qu'aprés l'envoi...mais c'est pas grave j'attend toujours vos indices :++:
-
Chimomo
- Membre Relatif
- Messages: 275
- Enregistré le: 17 Juin 2006, 09:23
-
 par Chimomo » 03 Aoû 2006, 11:15
par Chimomo » 03 Aoû 2006, 11:15
Tu dit que tu crois avoir démontré l'injectivité, n'es-tu pas sur de ton résultat ??
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 03 Aoû 2006, 11:55
par nada-top » 03 Aoû 2006, 11:55
:hein: en fait je crois que c'est juste ...voilà pour etre plus claire comment j'ai procédé pour la démontrer ...(en gros)
suposons qu'ils existent deux élément
)
et
)
tel que
 \neq(x',y'))
on pose

et

donc j'ai prouver par la suite que
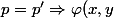 -\varphi(x',y')= x-x')
(simple à démontrer) et tel que
 \neq(x',y') \Rightarrow x \neq x')
...donc on peut en déduire que
,(x',y'))\in N\times N) \, : \, (x,y)\neq(x',y') \, \Rightarrow \, \varphi(x,y)\neq \varphi(x',y') \, \Longleftrightarrow)
[FONT=Comic Sans MS]
application injective[/FONT] c'est ça ??
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 03 Aoû 2006, 20:54
par nada-top » 03 Aoû 2006, 20:54
alors il y a personne ici pour me répondre :mur: :mur:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 03 Aoû 2006, 21:28
par nekros » 03 Aoû 2006, 21:28
Bonjour,
Pour montrer que A implique B montre que non(B) implique non(A)
Je crois que c'est bien ce que tu as fais.
Thomas G :zen:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 03 Aoû 2006, 21:29
par nekros » 03 Aoû 2006, 21:29
Que proposes-tu pour prouver la surjectivité ?
Thomas G :zen:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 03 Aoû 2006, 21:30
par nada-top » 03 Aoû 2006, 21:30
salut
oui c'est ça l'implication réciproque
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 03 Aoû 2006, 21:33
par nekros » 03 Aoû 2006, 21:33
Donc ce que tu as fait est correct, sauf erreurs de ta part dans les calculs :we:
De toute façon, tu as utilisé la bonne méthode.
Et pour la surjectivité ?
Thomas G :zen:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 03 Aoû 2006, 21:50
par nada-top » 03 Aoû 2006, 21:50
NON ne t'inquiète pas pour l'injectivité , il n'y a pas boucoup de calculs
alors pour prouver la surjectivité en général on peut considèrer un élément

de l'ensemble d'arrivée

et on doit prouver qu'il existe un élément
)
de l'ensemble du départ
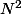
tel que
 = n)
... c'est ça ?? mais j'arrive pas à prouver ça :mur:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 03 Aoû 2006, 22:01
par nada-top » 03 Aoû 2006, 22:01
ah oui avant d'oublier ...il me parait un indice mais je sais pas comment je peux m'enservir :id:
on peut pas s'enservir de la somme
 = 1+2+...n= \frac{n(n+1)}{2})
car il me parait que les élément de l'ensemble d'arrivée s'écrivent sous cette forme ( +x qui me gène) :hum:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 04 Aoû 2006, 21:41
par nada-top » 04 Aoû 2006, 21:41
alors il y a quelqu'un pour m'aider à terminer cet exo :doh: :doh: :doh: j'espère que la question est claire .
-
Bouchra
- Membre Relatif
- Messages: 113
- Enregistré le: 13 Juil 2006, 15:38
-
 par Bouchra » 06 Aoû 2006, 14:03
par Bouchra » 06 Aoû 2006, 14:03
Une tite idée:
On va checher à montrer que pour tout n de IN, n peut s'écrire comme :
p(p+1)/2 + x avec p et x entiers et p>=x (p=x+y).
On a pour tout n entier naturel, il existe un unique p tq :
p(p+1)/2=
Donc n = p(p+1)/2 + x .
et comme (p+1)(p+2)/2-p(p+1)/2 = p+1 > n-p(p+1)/2 =x, ce p convient .
On a donc : Phi^(-1) (n) = (n-p(p+1)/2,p-n+p(p+1)/2)
Au fait, tu l'as trouvé où, cet exercice ?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Aoû 2006, 11:33
par nada-top » 07 Aoû 2006, 11:33
BONJOUR Bouchra :we:
merci pour cette bonne idée je crois l'avoir comprise à part un petit détail :
Donc n = p(p+1)/2 + x .
quelle(s) condition(s) tu as pris sur ce x , car si

, x peut etre = à
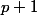
et ça ne convient pas je crois :hein:
Au fait, tu l'as trouvé où, cet exercice ?
:ptdr: tu peux dire un peu partout mais la solution nul part ..mais moi je l'ai découvert dans mon manuel d'analyse SM p.81 et p.87 partie ensemble et application et je l'ai eu aussi dans un devoir maison sans +x et ça etait tres facile .. c'est ce +x qui m'a bloqué.
-
Bouchra
- Membre Relatif
- Messages: 113
- Enregistré le: 13 Juil 2006, 15:38
-
 par Bouchra » 07 Aoû 2006, 16:21
par Bouchra » 07 Aoû 2006, 16:21
Bonjour,
nada-top a écrit: quelle(s) condition(s) tu as pris sur ce x , car si

, x peut etre = à
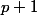
et ça ne convient pas je crois :hein:
Comme on a : il existe p tq p(p+1)/2 =x, d'où p>=x. Pas de problème donc :we:
:ptdr: tu peux dire un peu partout mais la solution nul part ..mais moi je l'ai découvert dans mon manuel d'analyse SM p.81 et p.87 partie ensemble et application et je l'ai eu aussi dans un devoir maison sans +x et ça etait tres facile .. c'est ce +x qui m'a bloqué.
Ok, j'avais jamais croisé cet exercice. Maintenant je l'ai plus ce livre :triste:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Aoû 2006, 20:39
par nada-top » 07 Aoû 2006, 20:39
AH oui je comprends mieux maintenant.... j'ai lu ça
p(p+1)/2 + x avec p et x entiers et p>=x (p=x+y).
et j'ai pas fait attention à la condition qui vient aprés donc

tq

merci beaucoup Bouchra :king2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
