Probabilités

bonjour j'ai une question à propos d'un exercice

On a X, Y, Z trois variables aléatoires indépendantes suivant une même loi géométrique de paramètre p sur N*

On a U=max(X,Y) et V=min(X,Y)

on me demande de calculer p(V > k)(c'est supérieur ou égal en fait mais je n'arrive pas à l'écrire)

j'ai retrouvé un exercice que l'on a fait pendant l'année où on écrivait de faire

p(V>k)= p(X>k)*p(Y>k) (car les variables sont indépendantes on peut faire le produit))(c'est supérieur ou égal aussi!hihi)
= (1-p)^(k-1) * (1-p)^(k-1)


je ne comprend pas pourquoi l'on fait ça et comment on justifie ces étapes?pourriez vous m'expliquer?
De plus la technique sera plus ou moins la même pour U si on veut p(UMerci bonne soirée

bon déjà je ne comprend pas à quoi sert ta variable Z, deux aurais suffit!

sinon le calcul en lui même c'est juste de reécrire les évennements:



comme les événnement sont indépendants on peut faire le produit simple (la vrai formule c'est celle de Baye : P(A et B) = P(A|B)p(B) ). Mais grace à l'indépendance la condition sachant B peut etre ignoré.

apres c'est juste du calcul avec la loi de probabilité géométrique :



comme p+q=1 on a le résultat que tu donne, pour le max c'est pareil il est plus petit que k ssi X et Y le sont.

Oh merci j'ai tout compris!C'est simple en fait merci beaucoup pour cette explication claire!

Puis-je poser une autre question de proba encore? je n'arrive pas à traduire le français en symboles mathématiques parfois alors que c'est bien souvent la clé pour éclaircir les problèmes!!

La situation est que l'on jette r jetons dans n boîtes avec n>3 de la façon suivante:
chaque jeton a la même probabilité de tomber dans chacune des boîtes et on suppose que les jetons sont lancés indépendemment les uns des autres

1Soit l'événement Ai "la ième boîte n'a pas reçu de jeton" Il faut calculer P(Ai)
j'ai utilisé la loi binomiale car pour moi soit la boîte ne reçoit rien soit elle reçoit quelque chose
Ca me donne
P(Ai)= *
=

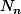
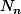
Et après on me demande de calculer E() avec le nnombre de boîtes avec 0 jetons
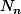
Pour m'aider on me dit que l'on peut exprimer en fonction des variables avec i allant de 1 à n et où prend les valeurs 0 et 1 et vaut 1 si l'événement est réalisé

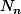
alors si je comprend bien est égal au nombre de fois où la variable prend la valeur 1 parmi les r lancers mais je bloque sur la transcription mathématiques

Ca ne doit pas être bien compliqué encore une fois mais à force de chercher j'y vois plus très clair!!

Une bonne âme pourrait m'aider à y voir mieux?

Meric d'avance et bonne soirée à toutes et à tous!

Il suffit de remarquer que

Aaaa bah oui c'est vrai parce que soit c'est égal à zéro et donc ça disparaît et il ne reste plus que les cas où =1
C'est évident!Merci beaucoup

Alors du coup j'ai calculer une espérance qui me paraît un peu bizarre...

J'ai E= k p(=k)

E= k)
enfin là je suis plus très sûr et ensuite ça donnerait

E=) car k=0 ou 1

ce serait alors
E=) + )
et après il faut faire intervenir p() qu'on a calculé avant dans la question précédente je pense
Est-ce bon ou pas je ne sais plus du tout si j'ai le droit de sortir la somme de la probabilité mais j'ai recherché un exo dans lequel je croyais qu'on avait déjà fait cela...je n'ai pas retrouvé, ça se trouve je suis trop dans l'exercice pour me rendre compte d'une grossière erreur

Merci de me donner votre avis

Oulala. Relis ce que tu écris pour te rendre compte que cela n'a pas de sens...

La bonne méthode est d'utiliser la linéarité de l'espérance. On obtient



Or est une variable de Bernoulli son espérance est donc égale à la probabilité .

Donc