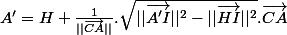merci Chan89 si apres il y a des impossibilités je devrai retomber dessus dans ce cas, bon là évidemment tout de suite j'en suis pas là
MLAM bon je continue là je viens de determiner le point K image du point I sur la droite passant par C et B et dans le même temps j'essaye de tout reprendre depuis le debut avec le dernier truc que j'ai trouvé ce matin de sorte que tout se trouve là sur ce post et en esperant que ce soit lisible
(bon et j'ai enlevé des truc inutiles que j'avais écrit)
mais faudra être patient car c'est long il reste pas mal de choses à faire
en fait là je continue de traiter l'énoncé comme si on connaissait les points A,B,C
->en fait l'énoncé par les points
mais à la fin je le traiterai comme si ce sont plutôt les distances AB,AC,BC qui sont données
-> en fait l'énoncé par les distances
puis pour conclure comme si ce sont plutôt les angles
,
,
qui sont donnés et un des cotés
->en fait l'énoncé par les angles et un coté
ENONCE PAR LES POINTS
Soient sont donnés les cinq objets suivants :
A,B,C trois points non alignés du plan affine définis sur le repere canonique et le rapport 
et la norme 
_____ description
tels que le point I est la secante de la médiane issue de C et du segment AB
le point 
avec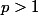 
et le point 
avec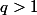 
le triangle A',B',I' est isocèle et le point I' est la secante de la médiane issue de I et du segment A'B'
on recherche les points A',B',I' et les angles 
et 
et 
et 
et 
___________________________________________
recherche de la solution de l'énoncé par les points
par ailleurs le triangle A',I',B' est isocèle de hauteur
les triangles I',A',I et I',B',B sont identiques et droits en I on obtiens donc
on pose le point H qui est l'image du point I sur la droite qui passe par les points A et A'
avec le vecteur V
ci dessous on note =v1.w1+v2.w2 le produit scalaire euclidien de deux vecteurs v=(v1,v2) et w=(w1,w2)
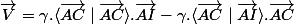
avec gamma
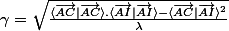
avec lambda
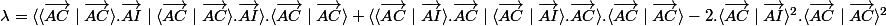
on verifie
on pose le point K qui est l'image du point I sur la droite qui passe par les points B et B'
avec le vecteur W
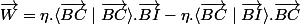
avec eta
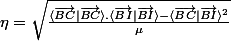
avec mu
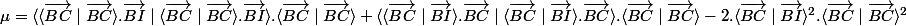
on verifie
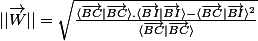
à partir de là trois cas peuvent se présenter et on doit traiter la question distinctement sur ces trois cas là
premier cas lorsque l'on vérifie H=A dans ce cas en fait on vérifie
deuxième cas lorsque l'on vérifie
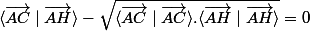
dans ce cas les vecteurs
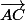
et
ont même direction et sens
troisième cas lorsque l'on vérifie
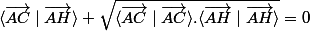
dans ce cas les vecteurs
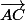
et
ont même direction mais de sens opposés
______________________________
ici je traite d'abord le troisième cas
troisième cas lorsque l'on vérifie
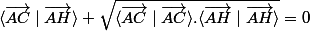
dans ce cas les vecteurs
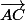
et
ont même direction mais de sens opposés
alors on obtiens le point A' selon
par