alphamethyste a écrit:1)dans ton énoncé tu ne dit pas clairement quels sont les données dont tu dispose
d'apres ce que j'ai compris seuls les distances AB AC et CB sont donnés
mais ça serai bien de le dire clairement
un enoncé doit être formulé par écrit et non se deviner avec un dessein
(en fait on a pas besoin d'un dessein pour dire ce que l'on a à dire )
l'ecrit est plus important que le visuel (toujours)
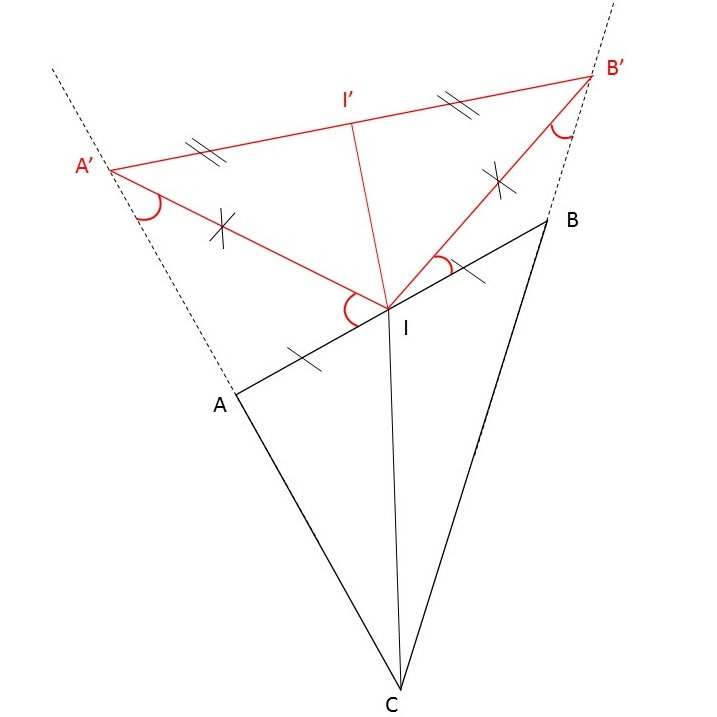
Humm désolée, je pensais que c'était clair que le début de l'énoncé, avec les "Soit" définit les données connues, et le "On cherche" les données que je ne connais pas.
Je ne savais pas ce qu'il était bien de dire ou non. Par exemple, le fait de dire que le triangle ABC est quelconque (et fait partie des données) sous-entend pour moi qu'on connaît toutes les longueurs et les angles, mais je ne me vois pas faire la liste de tout ça.
Ou encore, le fait de dire que IA'B' est isocèle en I, selon moi, rend inutile le fait de préciser que IA' et IB' sont des longueurs égales.
Et dernier exemple, le fait de dire que CI est la médiane qui coupe [AB] explicite clairement que les longueurs IA et IB sont égales. Ou alors je confonds la médiane avec autre chose, c'est possible aussi.
alphamethyste a écrit:2)ensuite tu dit que I est la sécante de la mediane en C et du segment AC
mais le probleme c'est que d'apres ton dessein AI=IB
et ça il faudrait que tu le dise car dans ton enoncé tu ne le dit pas
et ça n'est pas parce qu'il s'agit de la médiane en C que forcément on aura AI=IB
cette égalité n'est pas obligatoire en soi : c'est à toi de la decreter (ou pas) dans ton énoncé
La médiane issue de C coupe le segment opposé en deux parties égales, non ? Donc AI = IB. Je n'ai rien dit d'autre. Est-ce que c'est mal formulé ? J'aurais dû dire "issue de C" au lieu de "en C" ?
mlam a écrit:Soit un triangle quelconque ABC et sa médiane en C qui coupe [AB] en I.
Pour moi ça fait partie des données du problème, c'est pour ça que je me contente de préciser que c'est la médiane. (Cf. explications plus haut dans mon message).
Et le dessin permet justement de dissiper tout malentendu. J'entends bien que l'écrit est plus important que le visuel, mais il ne s'agit pas d'un exercice qu'on m'a donné dans le cadre du lycée, mais d'un souci au boulot que j'ai modélisé de cette manière. Et je ne passe pas mes journées à rédiger des énoncés mathématiques. D'où le dessin

alphamethyste a écrit:3)dans tous les cas pour determiner A',B',I' encore une fois le fait de connaitre juste un rapport ne suffit pas car ton triangle A'I'B' est isocèle
C'est le fait que AI'B' soit isocèle qui est dérangeant par rapport au fait que je donne uniquement des rapports ? J'avoue ne pas tout comprendre :/
Je ne comprends pas pourquoi on ne peut pas trouver de solution sachant qu'il y en a une. Quel que soit le triangle ABC, j'ai l'impression qu'il y a une solution unique, solution constituée d'un coefficient qui détermine la taille de IA'B', et d'une rotation pour placer ledit triangle.