Géométrie dans l'espace et suite

Bonjour, j' ai besoin d'aide et de correction pour deux exercices en maths. Le sujet est ci-dessous. Merci d'avance, je vous transmet mes réponses ensuite.

Exercice 1: géométrie dans l'espace

On se place dans l'espace muni d'un repère orthonormé.
On considère les points A(0,4,1), B(1,3,0), C(2,-1,-2), et D(7,-1,4)

1. Démontrer que les points A, B et c ne sont pas alignés.
2. Soit (delta) la droite passant par D et de vecteur directeur u(2,-1,3).
a) Démontrer que la doite (delta) est orthogonale au plan (ABC).
b) En déduire une équation cartésienne du plan (ABC).
c) Déterminer une représentation paramétrique de la droite (delta)
d) Déterminer les coordonnées du point H, intersection de la droite (delta) et du plan (ABC)

3. soit P1 le plan d'équation x+y+z=0 et P2 le plan d'équation x+4y+2=0
a) Démontrer que les plans P1 et P2 sont sécants.
b) Vérifier que la droite "d", intersection des plans P1 et P2 a pour représentation paramétrique
x=-4t-2
y=t
z=3t+2
avec t appartenant à R.
c)La droite "d" et le plan (ABC) sont-ils sécants?


Exercice 2: Suites

On considère la suite (Un) définie par Uo=1/2 et telle que pour tou entier naturel n, Un+1=(3Un)/(1+2Un)

1.a) Calculer U1 et U2
b) Démontrer, par récurrence , que pour tout entier naturel n, 0<Un.

2. On admet que, pour tout entier naturel n, Un<1.
a) Démontrer que la suite (Un) est croissante.
b) Démontrer que la suite (Un) converge.

3) Soit (Vn) la suite définie, pour tout entier naturel, n, par Vn= Un/(1-Un).
a) Montrer que la suite (Vn) est une suite géométrique de raison 3.
b) exprimer pour tout entier naturel n, Vn en fonction de n.
c) En déduire que pour tout entier n, Un=(3^n)/((3^n) +1).
d) Déterminer la limite de la suite (Un).

Pour l'exercice 1: Géométrie dans l'espace

On a pas terminer ce chapitre en cours avec notre professeur, il y a donc pas mal de chose qu'on a pas encore appris. On est sensé voir tout cela d'ici la fin de semaine.

1. le principe est-il le meme avec des points de coordonnée (x,y,z) ?

Pour l'exercice 2, sur les suites:

1. U1= (3*Uo)/(1+2*Uo)= (3*0.5)/(1+2*0.5)=3/4
U2=(3*U1)/(1+2*U1)=15/4

2. (J'ai un peu de mal avec la récurrence.. )
Je montre par récurrence que Pn: " 00
donc Po est vrai
hérédité: Soit n appartenant à N fixé
On suppose que Pn est vraie
Uo0 alors la suite est croissante
b) Si une suite est croissante et majoré alors elle converge, par conséquent on sait déjà qu'elle est croissante, montrons qu'elle est majorée. ( il faut que je retrouve la méthode)

3.a) Vn= (3^n)/(1-Un)
Vo= Uo/(1-Uo)= (1/2)/(1-(1/2))=1
V1= U1/(1-U1)= (3/4)/(1-(3/4))=3
la raison q=Vn+1/Vn=3/1=3
Alors la suite (Vn) est une suite géométrique de raison q=3 et de premier terme Vo=1.

Je vous tiens rapidement au courant pour la suite de l’exercice. Merci de m'aider

bonjour

il aurai mieux valu creer deux topics un pour chaque exercice ...

car là il faudra citer à chaque fois de quel exo on parle

pour l'exercice 1 question 1

il faut véfifier que tes vecteurs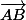 et 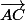ne soient pas colinéaires

pour ce faire j'ai une question : as tu vu le produit scalaire (euclidien) dans ton cours ?

tu comprend alors que si ces deux vecteurs là ne sont pas colinéaires alors dans ce cas les points A,B,C ne sont pas alignés

notons la convention de notation est le produit scalaire des deux vecteurs V et W

alors tes deux vecteurs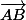 et 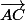ne sont pas colinéaires et que donc tes points A,B,C ne sont pas alignés
si et seulement si

à ce propos il n'est pas inutile de dire qu'en fait

tes deux vecteurs non nuls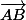 et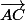

engendrent un angle que l'on notera exprimé en degrés

ou alors exprimé en radians (qui est l'unité angulaire mathématique )

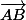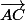-lorsque les deux vecteurs et ne sont pas colinéaires
et que en plus alors et dans ce cas les deux segments de droites AB et AC sont orthogonaux

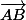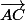-lorsque les deux vecteurs et ne sont pas colinéaires
et que en plus alors et dans ce cas les deux segments de droites AB et AC forment un angle aigue en A de valeur

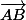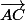-lorsque les deux vecteurs et ne sont pas colinéaires
et que en plus alors et dans ce cas les deux segments de droites AB et AC forment un angle obtus en A de valeur

par ailleurs en ce qui concerne les valeurs trigonométrique de cet angle tu vérifie







et tu vérifie

avant de continuer est-ce que tu vois l'utilité de l'utilisation du produit scalaire pour résoudre la question 1) ?

bon tout compte fait j'ai un peu de temps là alors je continue

pour la question 2)a) toujours exercice 1)

2. Soit (delta) la droite passant par D et de vecteur directeur
a) Démontrer que la droite est orthogonale au plan formé par les trois points A,B,C

le mieux (à la limite) est d'utiliser le produit vectoriel et de démontrer que



en effet si la droite est orthogonale au plan formé par les trois points A,B,C
alors dans ce cas

et sont colinéaires

par ailleurs en ce qui concerne la question 2)d) il n'est pas inutile non plus de déterminer de suite l'image H du point D sur le plan A,B,C (en fait l'intersection de la droite et du plan formé par les trois points A,B,C
afin de vérifier que effectivement les deux vecteurs et sont colinéaires

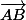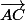pour se faire une méthode simple consiste à construire un repère de centre A et définis par les trois vecteurs et et

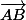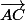pour ce faire tu construit l'endomorphisme dont la matrice M est définie par les trois vecteurs colonnes dans l'ordre ces trois vecteurs là et et

il s'agit alors dans un premier temps de déterminer les coordonnées du point D par rapport à ce repère là

pour ce faire tu pose la matrice colonne qui représente le vecteur

alors les coordonnées du point D par rapport à ce repère est donnée par les composantes de la matrice colonne N solution de l'expression

où ici il s'agit du vecteur colonne

alors la position du point H par rapport au repere canonique est donné par


et si tu applique la formule que je te donne tu obtiens donc H=(3;1;-2)

avec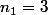 et 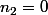de sorte que les trois points A,B et H sont alignés

je reviens plus tard pour la question 2)b)

en attendant as tu des questions et qu'as tu trouvé en appliquant ce que je t'ai dit ?

bon j'ai là tout de suite un peu de temps disponible donc je continue

on termine la question 2a)

on dois donc vérifier



c'est effectivement le cas









et on vérifie si la droite est orthogonale au plan formé par les trois points A,B,C
alors dans ce cas

et sont colinéaires

de sorte que



ce que l'on vérifie effectivement










et donc

Lency410 a écrit:Exercice 2: Suites

On considère la suite (Un) définie par Uo=1/2 et telle que pour tou entier naturel n, Un+1=(3Un)/(1+2Un)

1.a) Calculer U1 et U2
b) Démontrer, par récurrence , que pour tout entier naturel n, 00
donc Po est vrai
hérédité: Soit n appartenant à N fixé
On suppose que Pn est vraie
Uo0 alors la suite est croissante
b) Si une suite est croissante et majoré alors elle converge, par conséquent on sait déjà qu'elle est croissante, montrons qu'elle est majorée. ( il faut que je retrouve la méthode)

3.a) Vn= (3^n)/(1-Un)
Vo= Uo/(1-Uo)= (1/2)/(1-(1/2))=1
V1= U1/(1-U1)= (3/4)/(1-(3/4))=3
la raison q=Vn+1/Vn=3/1=3
Alors la suite (Vn) est une suite géométrique de raison q=3 et de premier terme Vo=1.

Je vous tiens rapidement au courant pour la suite de l’exercice. Merci de m'aider

1.b) L’hérédité consiste à montrer que si on suppose la propriété vraie, alors la propriété de rang suivant est également vraie.
Pour cela, suppose que , montre qu'alors :we:

2.a) Pour montrer la croissance de est croissante, exprime en fonction de pour justifier que .
2.b) Conséquence de la question précédente : la suite est croissante et majorée par (d'après l'hypothèse de la question 2.) cela implique donc que nécessairement elle converge.
3.a) En partant de l'expression de en fonction de , remplace l'expression de par la relation donnée dans l'énoncé (en fonction de ). Tu auras ainsi en fonction de . En regardant l'expression de en fonction de donnée dans la question, tu pourras trouver le réel (qui sera la raison) tel que :+++:
3.b) est une suite géométrique de premier terme et de raison donc quel que soit , .
3.c) Remplace l'expression de en fonction de n dans l'égalité liant et donnée en question 3.

bon j'ai un peu de temps là pour passer à la question suivante 2b)

Exercice 1: géométrie dans l'espace

On se place dans l'espace muni d'un repère orthonormé.
On considère les points A=(0,4,1), B=(1,3,0), C=(2,-1,-2), et D=(7,-1,4)

1. Démontrer que les points A, B et c ne sont pas alignés.
2. Soit (delta) la droite passant par D et de vecteur directeur u(2,-1,3).
a) Démontrer que la doite (delta) est orthogonale au plan (ABC).
b) En déduire une équation cartésienne du plan (ABC)

en fait on recherche des paramètres a,b,c,d tel que pour tout point de coordonnées (x,y,z) defini sur le repere canonique alors ce point appartiens au plan formé par les trois points A,B,C si et seulement si on vérifie ax+by+cz+d=0

cette équation est l'équation cartésienne de ce plan

notons par convention et et

on définit donc le système


et donc


on effectue des opérations sur les lignes du système pour avoir un système semblable

L3-2.L2->L3 c'est à dire qu'on transforme la ligne 3 en la remplaçant par la différence de la ligne 3 et de deux fois la ligne 2 et ce faisant on obtiens



puis L3+2.L1->L3 on obtiens



on peut poser a=1 puis en remplaçant les paramètres convenablement on obtiens



de sorte que est l'équation cartésienne de ce plan

je reviens dans un tout petit instant pour la question 2c) suivante ...

à présent on passe aux questions 2c) et 2d)

on a déjà répondu à la question 2d) et on avait trouvé H=(3;1;-2)

par ailleurs sur le même topic Captain Nuggets viens de faire l'exercice 2)

moi je m'occupe de l'exercice 1)

Exercice 1: géométrie dans l'espace

On se place dans l'espace muni d'un repère orthonormé.
On considère les points A(0,4,1), B(1,3,0), C(2,-1,-2), et D(7,-1,4)

1. Démontrer que les points A, B et c ne sont pas alignés.
2. Soit (delta) la droite passant par D et de vecteur directeur u(2,-1,3).
a) Démontrer que la droite (delta) est orthogonale au plan (ABC).
b) En déduire une équation cartésienne du plan (ABC).
c) Déterminer une représentation paramétrique de la droite (delta)
d) Déterminer les coordonnées du point H, intersection de la droite (delta) et du plan (ABC)

bon en ce qui concerne la question 2c) de quoi s'agit-il ?

en fait toute droite de l'espace affine peut être définie par un point et un vecteur

ici dans l'exo il s'agit du point et du vecteur

ici pour cet exo les coordonnées du point D sont définies par rapport au repere canonique

et les coordonnées du vecteur sont définies par rapport à la base canonique

alors un point P de coordonnées (x,y,z) défini sur ce même repere canonique appartiens à la droite si et seulement si tel que

et donc et donc

il résulte donc que l'on obtiens le système d'équation




par conséquent désigne l'équation paramétrique de la droite

bon je reviens tout de suite pour la suite des questions de cet exercice 1

salut alphamethyste
est possible d utiliser le produit vectoriel pour déterminer l équation du plan ABC) et de la droite

merci

salut olivier!

je me suis endormi sur la table (merci de m'avoir réveillé ...) je vais passer à la question 3 tout de suite

mais là vite fait pour te répondre

olivier 2020 a écrit:salut alphamethyste
est possible d utiliser le produit vectoriel pour déterminer l équation du plan ABC) et de la droite

merci

mais pourquoi ? (en fait non) pour l'equation du plan , il suffit d'utiliser les coordonnées des trois points A,B,C (comme c'est écrit plus haut)

et pour la droite celle ci est définie uniquement par le point D et le vecteur U

par contre comme c'est écrit plus haut j'ai utilisé le produit vectoriel pour determiner

le point H=(3;1;-2)

bon je continue là pour la question 3a)

Exercice 1: géométrie dans l'espace

On se place dans l'espace muni d'un repère orthonormé.
On considère les points A(0,4,1), B(1,3,0), C(2,-1,-2), et D(7,-1,4)

1. Démontrer que les points A, B et c ne sont pas alignés.
2. Soit (delta) la droite passant par D et de vecteur directeur u(2,-1,3).
a) Démontrer que la doite (delta) est orthogonale au plan (ABC).
b) En déduire une équation cartésienne du plan (ABC).
c) Déterminer une représentation paramétrique de la droite (delta)
d) Déterminer les coordonnées du point H, intersection de la droite (delta) et du plan (ABC)

3. soit P1 le plan d'équation x+y+z=0 et P2 le plan d'équation x+4y+2=0
a) Démontrer que les plans P1 et P2 sont sécants.

bon alors deux plans d'équations cartesiennes

P1:=x+y+z=0 et P2:=x+4y+2=0

pour démontrer que P1 et P2 sont sécants alors dans un premier temps on recherche deux points que l'on va noter et et qui appartiennent à ces deux plans

puis dans un second temps on doit démontrer que alors le point de coordonnée sur le repere canonique appartiens à ces deux plans

démonstration

selon P2 alors x+4y+2=0 donc

et selon P1 et P2 simultanément alors x+y+z=0 donc

on obtiens

on peut poser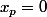 de sorte que selon P2 on obtiens

et selon P1 et P2 simultanément alors

de sorte que

on peut poser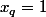 de sorte que selon P2 on obtiens

et selon P1 et P2 simultanément alors

de sorte que

on obtiens le système



donc le système



alors selon P1 on vérifie x+y+z=0 effectivement

et selon P2 on vérifie x+4y+2=0 effectivement

bon je reviens pour terminer il reste plus que les questions 3b) et 3c)

salut alphamethyste


http://homeomath2.imingo.net/planequ.htm

merci

salut alphamethyste
pardonner moi
c este juste pour l utilisation du produit vectoriel ( très pratique )

merci

bah pour determiner le point H oui je l'ai utilisé mais pour le reste non il ne faut pas l'utiliser

on te donne trois points non alignés et en deduire l'equation cartesienne de ce plan donc pour cela il faut voir comment je m'y suis pris (inutile d'aller en terre ennemie )

as tu vu mes posts ici ? tu vois pourquoi je l'ai utilisé et pourquoi ensuite je m'en suis pas servi ?

bon là il reste deux questions 3b) et 3c) à terminer -bon tout à l'heure - mais je comprend pas trop ta fixation pour utiliser le produit vectoriel quand il est d'aucune utilité

Bonjour, merci de vos conseils, ils m'ont permis de comprendre et ainsi je me suis bien m'avancer. Si j'ai des questions, je n’hésiterais pas.

Juste une question, ce n'est pas en lien avec ces deux exercices, mais es ce que pour justifier que deux droites sont sécantes en un point, il faut simplement démontrer qu'elles ne sont pas parallèles?

attention : dans l'espace il y a des droites qui bien que non parallèles, ne sont pas pour autant sécantes

donc pour determiner si deux droites sont sécantes (et à quel endroit elles le sont ) tu dois utiliser les representations parametriques de ces droites

d'ailleurs pour determiner le segment PQ avec P appartiens à une droite D1 et Q appartiens à une droite D2
avec D1 et D2 sont des droites non sécantes et non parallèles et tel que la distance PQ est la plus petite possible là encore tu dois travailler avec les informations que te donne les representations parametriques de ces deux droites

en fait toute les informations concernant une droite sont données par sa representation parametrique

tu as vu plus haut comment on la determine

enfin en ce qui concerne ce que j'ai dit plus haut si on n'avait pas verifié que la droite Delta etait perpendiculaire au plan A,B,C je n'aurai pas utilisé le produit vectoriel pour determiner le point H qui appartiens simultanément au plan A,B,C et à la droite Delta

mais plutôt j'aurai utilisé l'équation cartésienne du plan A,B,C (dont tu as vu comment il se determine) et la representation parametrique de la droite Delta

salut alphamethyste
est il possible de terminer la correction des deux questions
3b) et 3c)

merci beaucoup

oui j'avais oublié de les faire ...
ce soir camarade Olivier ... merci de me l'avoir dit
je reprend ce soir ...
excuse là j'écoute de la zic (en fait j'ai pas dormi depuis hier matin , mais bon je vais pas dormir juste je fais une pause camarade )

j'écoute un peu de Punk là (ça va pas trop avec les maths)

c'est bien c'est Trisomie21 The Last Song https://www.youtube.com/watch?v=A3ZVZVMIG7g

je reprend mais ce soir c'est ok (en fait j'ai pas besoin de dormir : j'arrive à tenir une semaine entière )
mais un peu de pause zic oui là ...

bon je reprend et encore désolé pour l'oubli

3. soit P1 le plan d'équation x+y+z=0 et P2 le plan d'équation x+4y+2=0

b) Vérifier que la droite "d", intersection des plans P1 et P2 a pour représentation paramétrique
x=-4t-2
y=t
z=3t+2
avec t appartenant à R

dans le traitement de la question 3a) on donné les points et

la droite "d" est donc définie parle point P et le vecteur directeur



un point R de coordonnées sur le repère canonique (x,y,z) appartiens à la droite "d" si et seulement si il existe un réel t tel que

donc donc



et donc

avec t un réel

et on doit démontrer que cette représentation paramétrique est équivallente à celle ci

x=-4t-2
y=t
z=3t+2

avec t un réel

on peut poser k=-4k-2 de sorte que

et en remplaçant t par cette égalitée sur cette représentation paramétrique là

x=-4t-2
y=t
z=3t+2

on obtiens



avec k un réel

ce qui est identiqueà la représentation paramétrique que l'on a déterminé

bon je reviens pour la derniere question 3c)

juste je fais une pause clope

bon je termine la dernière question

c)La droite "d" et le plan (ABC) sont-ils sécants?

la réponse est NON

on avait établit que l'équation cartésienne du plan formé par les trois points A,B,C est



et la représentation paramétrique de la droite "d" est



avec t un réel et donc en fait



alors si la droite "d" est sécante au plan formé par les trois points A,B,C alors on devrait vérifier

ce qui est FAUX

Bonjour, j'ai une question,
Pour l'exercice 2:à la question 3)b.
Vn=Uo*q^n
donc Vn=1/2*q^n
c'est bien cela ?

Du coup, pour la question 3)c.
1/2*q^n=Un/(1-Un)
Je n'arrive pas à déduire que Un=3Un/(3^n+1)
... besoin d'explications supplémentaires.


Merci d'avance.