Bonsoir à tous,
Je suis nouveau sur le forum, donc j'me présente en même temps que de poster ma demande...Robin, 17 ans, étudiant en sciences appliquées, terminale.
Alors, voilà mon problème...Dans le but de préparer mon année scolaire 2007-2008 je me retrouve avec un travail de vacances sur les bras. J'aime bien bosser, je pense beaucoup à mes études, donc ça me dérange pas...Par contre ce qui me dérange, c'est quand j'arrive vraiment pas à trouver une réponse après des heures de réflexion. Un ami m'a parlé de votre forum, du coup bah j'viens vous appeler à l'aide sur les 2/3 problèmes de suites que je rencontre.
voici les énnoncés qui me posent un réel problème (je n'ai aucune formules mis à part Un= u1+(n-1).r et Un= u1.q^n-1) :
1) Cinq nombres sont en progression arithmétique. Calculer ces nombres en sachant que leur somme est 124 et que la somme des deux premiers est 38.
2) Calculer 4 nombres en progression arithmétique dont la somme est 36 et tels que le plus grand vaut 5 fois le plus petit.
3) Déterminer 5 nombres en progression géométrique tels que la somme des 3 premiers est 30 et la somme des 3 derniers est 120.
Donc, si vous pouviez soit m'éclairer sur les formules et/ou développements à utiliser, soit me donner les réponses en m'expliquant précisément la méthode de façon à ce que je puisse les refaire moi-même par la suite ça serait plus que sympathique.
Merci d'avance, Robin.
Problèmes avec les suites géométriques/arithmétiques.
7 messages
- Page 1 sur 1
salut,
pour le 1er soient a,b,c,d,e les cinq nombres en progression arithmetique
tu peux ecrire que:
avec r la raison de la suite
a=c-2r
b=c-r
d=c+r
e=c+2r
et essayer à partir de ça de traduire ton ennoncé
a+b+c+d+e=124
a+b=38
...
je pars bosser donc je n'ai pas trop le temps de rediger quelqu'un le fera peut-être
pour le 1er soient a,b,c,d,e les cinq nombres en progression arithmetique
tu peux ecrire que:
avec r la raison de la suite
a=c-2r
b=c-r
d=c+r
e=c+2r
et essayer à partir de ça de traduire ton ennoncé
a+b+c+d+e=124
a+b=38
...
je pars bosser donc je n'ai pas trop le temps de rediger quelqu'un le fera peut-être
Bonjour
1)
Soit a-2r; a-r; a: a+r et a+2r
S = 5a = 124=> a =124/5(1)
a-2r +a-r = 2a -3r = 38 ou 2a - 3r = 38(2)
(2) 248/5 -3r = 38<=> 3r = 248/5-38=(248-190)/5=58/5 et r=58/15
2)Soit a-r; a: a+r; a+2r
S=4a +2r =36 ou 2a +r = 18(1)
a+5r = 4a -4r<=>-3a +9r = 0(2)
Il suffir de résoudre le système
3)Soit a; aq; aq²;aq³:aq^4 ('q#0)
S1= a(1+q+q²) = 30(1)
S2:aq²+aq²+aq^^4= 120
aq²(1+q+q²) =120 (2)
Tu trouveras facilement q puis a puis les 5 nombres
1)
Soit a-2r; a-r; a: a+r et a+2r
S = 5a = 124=> a =124/5(1)
a-2r +a-r = 2a -3r = 38 ou 2a - 3r = 38(2)
(2) 248/5 -3r = 38<=> 3r = 248/5-38=(248-190)/5=58/5 et r=58/15
2)Soit a-r; a: a+r; a+2r
S=4a +2r =36 ou 2a +r = 18(1)
a+5r = 4a -4r<=>-3a +9r = 0(2)
Il suffir de résoudre le système
3)Soit a; aq; aq²;aq³:aq^4 ('q#0)
S1= a(1+q+q²) = 30(1)
S2:aq²+aq²+aq^^4= 120
aq²(1+q+q²) =120 (2)
Tu trouveras facilement q puis a puis les 5 nombres
Merci beaucoup du coup de main, ça fait plaisir. Par contre, j'ai pas dutout compris ce qu'il fallait que je fasse une fois que j'ai ça :
Trouver Q, oui, mais comment ? %)
oscar a écrit:3)Soit a; aq; aq²;aq³:aq^4 ('q#0)
S1= a(1+q+q²) = 30(1)
S2:aq²+aq²+aq^^4= 120
aq²(1+q+q²) =120 (2)
Tu trouveras facilement q puis a puis les 5 nombres
Trouver Q, oui, mais comment ? %)
re,
tu prends 5 nombres a,bc,d et e en progression geometrique
on appelle q la raison
donc
b=aq
c=aq²
d=aq^3
e=aq^4
on dit que a+b+c=30 a+aq²+aq^3=30 (en mettant a en facteur) a(1+q+q²)=30 1+q+q²=30/a (1)
on dit egalement que c+d+e=120 aq²+aq^3+aq^4=120 (en mettant aq² en facteur) aq²(1+q+q²)=120 (2)
on a donc
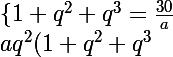=120)
on remplace 1+q+q² par 30/a ds la 2e ligne )
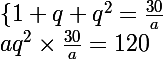
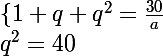
...
tu va obtenir q est donc ensuite la valeur de a et donc b,c,d et e
tu prends 5 nombres a,bc,d et e en progression geometrique
on appelle q la raison
donc
b=aq
c=aq²
d=aq^3
e=aq^4
on dit que a+b+c=30 a+aq²+aq^3=30 (en mettant a en facteur) a(1+q+q²)=30 1+q+q²=30/a (1)
on dit egalement que c+d+e=120 aq²+aq^3+aq^4=120 (en mettant aq² en facteur) aq²(1+q+q²)=120 (2)
on a donc
on remplace 1+q+q² par 30/a ds la 2e ligne )
...
tu va obtenir q est donc ensuite la valeur de a et donc b,c,d et e
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
