Intersection de deux cercle : coordonées sphériques

[kervizic]

Bonjour a tous,

Bon pour commencer je vous annonce de suite que je ne suis pas une flèche en math, je suis actuelement en école d'ingé mais issu d'un BTS.

J'ai un probleme a solutioner. Je dois definir (pour un programme) si deux route se coupe (route effectuée par des avion definie par deux points en coordonées polaires)
J'ai pensé a chercher les points d'intersection des deux cercle defini par les points des routes, et de verifier que ces points sont bien sur les portions de cercles qui definissent la route.
Hors je n'arrive pas a trouver comment definir ces points d'intersection ....

Si quequ'un a compris mon probleme et qu'il a de quoi m'orienter je suis preneur.
Bonne vacance a ce qui y sont et bon courage aux autres !
Cordialement, Manu.

[Ben314]

Salut,
Je ne sais pas si c'est le plus simple, mais perso, je procèderait de la façon suivante :
Etant donné deux points D (départ) et A (arrivé) non antipodaux de la sphère connu en coordonnées sphérique, on calcule leur coordonnées cartésiennes puis l'équation du plan passant par A,D et O (centre de la sphère) : c'est dans ce plan qu'est contenu la geodésique de A à D (i.e. la "ligne droite").
Idem pour les deux autres points D' et A' puis en cherchant l'intersection des deux plans, on en déduit les deux points d'intersection des deux géodésique.

Jusque là, c'est facile, mais le problème, c'est que chaque avion ne parcours qu'un arc de cercles (ce que tu appelle "un segment") et pas le cercle complet. Il faut donc regarder si un des deux points d'intersection des deux cercle est situé sur les deux arcs à la fois et pour ce faire, il faut déterminer "calculatoirement" ces arcs.
Pour ce faire, on peut calculer les coordonnées du millieu I de [AD] et constater que, pour tout point M de l'arc qui nous interesse de A à D vérifie (produit scalaire). Idem pour A' et D'.
Il n'y a plus qu'à tester ces inégalités avec les deux points d'intersection des deux cercles.

[kervizic]

Re-bonjour,

Alors pour se qui est des plan j'ai cru comprendre et vais regarder dans cette direction (ecxuse moi d'avance si je n'utilise pas les termes matheux mais ce n'est vraiment pas mon domaine de prédilection).

Pour résumé je dois determiner les deux plan passant chaqun par les deux point de la route ainsi que par le centre de la terre, en deduire la droite passant par le centre de la terre et apartenant au deux plan et enfin trouver les coordonée spherique de cette droite.

je pense que si j'arrive a ce niveau une simple verification que le point en question est pour chaqune des route comprise entre les 2 lat des points et les deux long des points devrait fair l'affaire non ?

Corrigé moi si je me trompe de beaucoup.

Merci pour l'idée en tout cas j'essay de voire ce que je peux faire.

[Ben314]

Pour résumé je dois determiner les deux plan passant chaqun par les deux point de la route ainsi que par le centre de la terre, en deduire la droite passant par le centre de la terre et apartenant au deux plan et enfin trouver les coordonée spherique de cette droite.

Là, c'est O.K. (et je ne suis pas sûr qu'il soit obligatoire de "reconvertir" l'équation de la droite en coordonnées sphérique de deux points, par contre, il doit faloirs d'une façon ou d'une autre trouver l'intersection de la droite et de la sphère)

je pense que si j'arrive a ce niveau une simple verification que le point en question est pour chaqune des route comprise entre les 2 lat des points et les deux long des points devrait fair l'affaire non ?

Justement, là, en ce qui concerne les latitudes, ça ne marche pas : pour aller de Paris à New-York (latitudes sensiblement égales) le chemin le plus court passe trés au nord de cette latitude là donc, en général, les latitudes du chemin le plus court pour aller d'un point à un autre ne restent pas comprises entre les latitudes des points de départ et d'arrivé.
Par contre, il me semble que c'est correct pour les longitudes, modulo le fait que, pour aller de 150ouest à 160est, on passe évidement par 180ouest=180est et pas par 0ouest=0est !

C'est pour ça que je conseillait de faire la vérif plutôt avec des coordonnées cartésiennes que sphériques.

[kervizic]

ustement, là, en ce qui concerne les latitudes, ça ne marche pas : pour aller de Paris à New-York (latitudes sensiblement égales) le chemin le plus court passe trés au nord de cette latitude là donc, en général, les latitudes du chemin le plus court pour aller d'un point à un autre ne restent pas comprises entre les latitudes des points de départ et d'arrivé.
Par contre, il me semble que c'est correct pour les longitudes, modulo le fait que, pour aller de 150ouest à 160est, on passe évidement par 180ouest=180est et pas par 0ouest=0est !
.

J'ai pas vraiment compris ce que tu veux me dir. Pour simplifier tous mes calculs j'ai converti toutes les coordonées en decimal 15°30' Nord donne 15.5 et la meme au sud donnera -15.5
apres etant donné qu'il n'y a jamais plus de 90° d'ecart entre chaques points on peut facilement savoir entre quoi et quoi regarder.(oui desolé je n'ai pas precisé mais quant je dis route c'est en fait portion de route car elle est decomposée en plusieurs points. Bien evidement ces routes sont etudiées portions par portions)

Par contre si tu a des lien util pour comprendre comment fonctionne les plan et leur intersection je suis preneur car la je rame .....

En tout cas merci de t'interresser a mon probleme. Bonne continuation.

[Ben314]

Bon, tu commence par calculer les coordonnées cartésiennes et des points A et D à l'aide de leur coordonnées sphériques.
Le plan passant par O,A et D a alors pour équation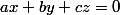 où (produit vectoriel), c'est à dire .
Tu procède de même pour trouver les coefficients de l'équation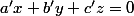 du plan passant par O,A' et D'.
L'intersection des deux plans contient bien sûr le point O, mais aussi le point P tel que .
Sauf que P n'est pas forcément sur la sphère. Pour trouver un point de la droite (OP) sur la sphére, il suffit de diviser les 3 coordonnées de P par la norme de , c'est à dire par . Cela te donne un des deux point d'intersection M, l'autre M' étant évidement celui dont les coordonnées sont l'opposé de celle de M.
Tu n'as plus qu'a regarder si les produits scalaires mentionnée dans le précédent post sont ou pas positifs.

[kervizic]

Je te demande une aide pour me guider tu me realise gracieusement toute la resolution du probleme !!! reste a coder ca et a voir si ca marche ...

Je te remercie tout plein, je te tiens au courant de l'avancement.

[kervizic]

Comme promis voila le code en python: ca poura peut etre aider quelqu'un si google veut bien le porter jusqu'ici.

Code: Tout sélectionner

def round (num) :
   getcontext().prec = 25
   num = Decimal(str(num)).quantize(Decimal('.000000000000001'))
   return float(num)
   
def sphericalToCartesian (lat,long):
   # converts spherical coordinates to cartesian coordinates in a point
   lat = radians(float(lat)) # converts degrees to radians
   long = radians(float(long))
   x = cos(lat) * cos(long)
   y = cos(lat) * sin(long)
   z = sin(lat)
   coordinate = {
      'x' : x,
      'y' : y,
      'z' : z
      }
   return coordinate

def findPlane (lat1,long1,lat2,long2):
   #calculate the Cartesian coordinates (x, y, z) points 1 and 2
   #using their spherical coordinates
   c1 = sphericalToCartesian(lat1,long1)
   c2 = sphericalToCartesian(lat2,long2)
   print c1
   print c2
   # the point 0 is the center of the earth
   # the plane through 0, c1 and c2 then the equation ax + by + cz = 0
   # a = y1 * z2 - z1 * y2
   # b = z1 * x2 - x1 * z2
   # c = x1 * y2 - y1 * x2
   a = c1['y'] * c2['z'] - c1['z'] * c2['y']
   b = c1['z'] * c2['x'] - c1['x'] * c2['z']
   c = c1['x'] * c2['y'] - c1['y'] * c2['x']
   plane = {
      'a' : a,
      'b' : b,
      'c' : c
      }
   return plane

def findIntersection(line1 ,line2) :
   """
   line consists of two points defined by latitude and longitude :
   line = {
      'lat1' : lat1,
      'long1' : long1,
      'lat2' : lat2,
      'long2' : long2
      }
   in decimal
   """
   # find the plane of the line in cartesian coordianates
   p1 = findPlane(line1['lat1'],line1['long1'],
      line1['lat2'],line1['long2'],)
   p2 = findPlane(line2['lat1'],line2['long1'],
      line2['lat2'],line2['long2'],)
   # The intersection of two planes contains of course the
   # point of origin, but also the point P : (x,y,z)
   # x = b1 * c2 - c1 * b2
   # y = c1 * a2 - a1 * c2
   # z = a1 * b2 - b1 * a2
   x = p1['b'] * p2['c'] - p1['c'] * p2['b']
   y = p1['c'] * p2['a'] - p1['a'] * p2['c']
   z = p1['a'] * p2['b'] - p1['b'] * p2['a']
   
   norme = sqrt(x**2+y**2+z**2)
   lat1 = degrees(asin(round(z/norme)))
   long1 = degrees(atan2(round(y),round(x)))
   lat2 = - (lat1)
   if long1 <= 0 :
      long2 = long1 + 180
   else :
      long2 = long1 - 180
   intersection1 = {'latitude' : lat1, 'longitude' : long1}
   intersection2 = {'latitude' : lat2, 'longitude' : long2}
   print ''
   print 'point trouve :'
   print intersection1
   print intersection2

# test with Google Erath point
p11=convertCoordinate ('325111N0925021W')
p12=convertCoordinate ('385942N0811837W')
p21=convertCoordinate ('394023N0915033W')
p22=convertCoordinate ('312426N0843429W')
p=convertCoordinate ('353843N0880419W')
   
line1 = {
   'lat1' : p11['latitude'],
   'long1' : p11['longitude'],
   'lat2' : p12['latitude'],
   'long2' : p12['longitude']
   }   
line2 = {
   'lat1' : p21['latitude'],
   'long1' : p21['longitude'],
   'lat2' : p22['latitude'],
   'long2' : p22['longitude']
   }   
findIntersection(line1 ,line2 )   
print 'point lu:'
print p

et ce que ca donne :

Code: Tout sélectionner

{'y': -0.83903345439193344, 'x': -0.041610525806541399, 'z': 0.5424863376650535}
{'y': -0.76827939148300906, 'x': 0.11742222927802898, 'z': 0.62925256987466904}
{'y': -0.76930191722629993, 'x': -0.024747504894235731, 'z': 0.63840592192855561}
{'y': -0.84966180093676158, 'x': 0.080694906765257909, 'z': 0.52111721910818232}

point trouve :
{'latitude': -35.646949336459706, 'longitude': 91.93333953229957}
{'latitude': 35.646949336459706, 'longitude': -88.06666046770043}
point lu:
{'latitude': 35.645277777777778, 'longitude': -88.071944444444441}


A quelques chouillas pres on retombe sur les bon nombres (précision de lecture pas top dans google earth).

Encore un grand merci a toi Ben314.