Courbes sphériques
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
albantor30
- Membre Naturel
- Messages: 25
- Enregistré le: 20 Avr 2006, 18:23
-
 par albantor30 » 20 Avr 2006, 22:16
par albantor30 » 20 Avr 2006, 22:16
Bonjour !
J'aurais aimé savoir s'il y avait une forme générale pour toutes les équation des courbes appartenant à la surface d'une sphère. J'ai déja trouvé celle-ci :
) sin\left(g(x)) \\ y = R sin\left(f(x)) sin\left(g(x)) \\ z = R cos\left(g(x)))
Mais je ne sais pas si c'est la meilleure. Et n'y aurait-il pas moyen d'exprimer plus simplement :
 sin\left(f(x)) \\ y = R sin\left(x) sin\left(f(x)) \\ z = R cos\left(f(x)))
Mon but est en fait de trouver la géodésique sur la sphère sans utiliser la formule générale des géodésiques.
Merci !
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Avr 2006, 10:19
par Pythales » 21 Avr 2006, 10:19
Si u est l'angle du rayon avec oz, et v l'angle de la projection du rayon sur xoy avec ox, on a :
x=R sinu cosv
y=R sinu sinv
z=R cosv
d'où ds=...
(Je suppose que tu sais déja que les géodésiques sont des grands cercles. C'est un problème de calcul des variations)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Avr 2006, 11:06
par Pythales » 21 Avr 2006, 11:06
On trouve pour l'élément de courbe :
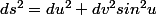
Le plus simple est d'arriver à montrer que les géodésiques sont l'intersection de la sphère avec des plans passant par l'origine, c.à.d une relation entre u et v de la forme :
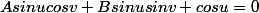
-
albantor30
- Membre Naturel
- Messages: 25
- Enregistré le: 20 Avr 2006, 18:23
-
 par albantor30 » 21 Avr 2006, 17:21
par albantor30 » 21 Avr 2006, 17:21
Ok merci. Mais est ce que ma coubre
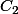
est suffisante pour désigner toute courbe continue appartenant à la sphère (à une symétrie près) ou y en a-til de plus complètes ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Avr 2006, 18:49
par Pythales » 21 Avr 2006, 18:49
Toute courbe sur la sphère est définie par une relation
=0)
ou, ce qui revient au même :

et
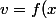)
. Il est souvent plus simple d'exprimer une relation entre x et y par une équation implicite ou une représentation paramétrique, plutôt que par y=f(x)
-
zorg
- Membre Naturel
- Messages: 78
- Enregistré le: 21 Avr 2006, 09:17
-
 par zorg » 21 Avr 2006, 19:53
par zorg » 21 Avr 2006, 19:53
@Pythales: ce que tu dis ne me semble pas exact. Toute courbe sur la sphère n'est pas définie par l'équation implicite
=0$)
. Ca c'est plutôt l'équation d'une surface.
@Albantor toute courbe sur la sphère est effectivement décrit par tes formules donnant
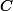
. C'est tout simplement la composée d'une courbe paramétrée
,g(x))$)
avec le paramétrage en sphérique de la sphère.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Avr 2006, 21:02
par Pythales » 21 Avr 2006, 21:02
Quand je dis que la courbe est définie par g(u,v)=0, j'entends bien sûr que cette relation doit compléter les équations de la surface, à savoir :
x=Rsinu cosv
y=Rsinu sinv
z=Rcosv
Se donner u, par exemple, détermine v, et donc x, y et z
OK ?
-
zorg
- Membre Naturel
- Messages: 78
- Enregistré le: 21 Avr 2006, 09:17
-
 par zorg » 21 Avr 2006, 21:38
par zorg » 21 Avr 2006, 21:38
@Pythales tu veux dire que la courbe sur le plan est définie implicitement par g(u,v)=0 puis ensuite on l'envoie sur la sphère par les coordonnées sphériques ?
En tout cas je ne pense pas que l'on décrive ainsi TOUTES les courbes de la sphère. De même la courbe C2 donnée par Albantor ne décrit pas TOUTES les courbes puisqu'il part d'une courbe dite cartésienne ie y=f(x) qui elle-même ne sont pas toutes les courbes du plan.
De façon générale, soit la surface S décrit par le paramétrage x=f(u,v) y=g(u,v) et z=h(u,v). Toutes les courbes tracées sur la surface de S sont décrites par les équations paramétriques
x=f(u(t),v(t))
y=g(u(t),v(t))
z=h(u(t),v(t))
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 22 Avr 2006, 12:05
par Pythales » 22 Avr 2006, 12:05
Je crois qu'on est d'accord, car éliminer t entre u=u(t) et v=v(t) conduit à une relation de la forme g(u,v)=0
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
 par serge75 » 22 Avr 2006, 12:11
par serge75 » 22 Avr 2006, 12:11
A condition de pouvoir l'éliminer, or la réponse générale est loin d'être triviale.
Il est faux de penser que toute courbe du plan puisse avoir une équation f(x,y)=0.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
