Courbes en coordonnées sphériques

par **Anonyme** » 05 Mai 2013, 10:13

Bonjour
J'ai la un exercice assez compliqué à résoudre et dont je n'ai aucune idée de comment faire :marteau: .

Je mets l'image suivante pour qu'on réfléchisse tous avec les mêmes définitions :

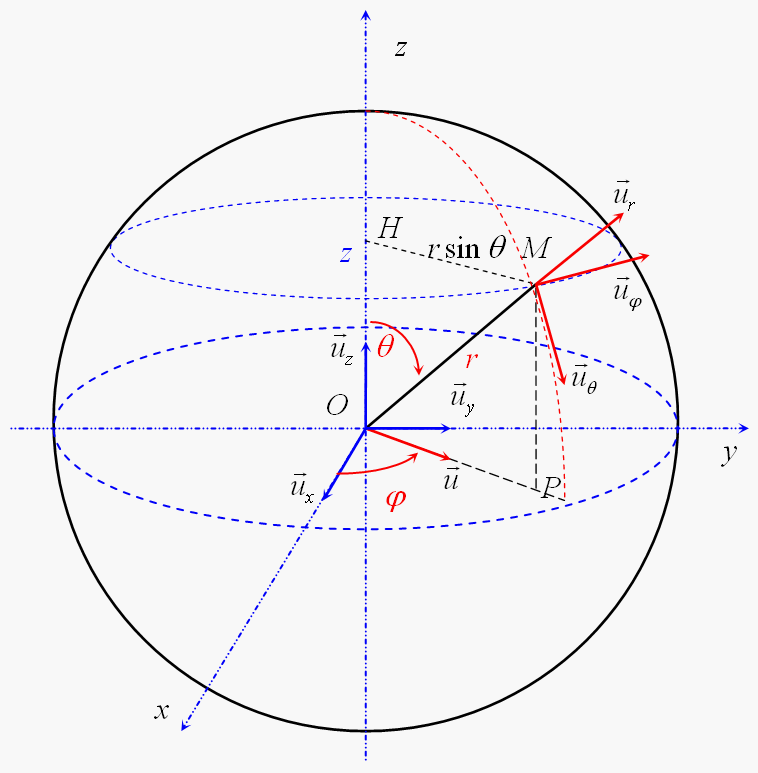
Soit R(O, r,phi,theta) un repère sphérique.
Soit S la sphère de rayon r et de centre O.

Soient cinq points connus exprimés dans R : A(r, 0, 0) , B(r, 0, pi/2), C(r, phi1, theta1), D(r, phi2, theta2).
Soit Delta1 la courbe contenue dans S et qui passe par les points A et B.
Soit Delta2 la courbe contenue dans S et qui passe par les points C et D.

Quels sont les points où se croisent Delta1 et Delta2 ? Exprimez les dans R.

J'imagine qu'il faut trouver les équations de ces deux courbes et puis égaliser les équations et résoudre celle qu'on obtient. Au final il y a normalement une infinité de points solutions.

Merci à ceux qui aident, et ceux qui on pensait pouvoir m'aider :we: . Et puis même si vous n'avez qu'un semblant d'aide, ça peut toujours dépanner. Merci

par **chan79** » 05 Mai 2013, 11:47

Salut
Delta1 et Delta2 sont des cercles de centre O ?

par **Dlzlogic** » 05 Mai 2013, 11:49

Bonjour,
Je suppose que par "courbe" il faut comprendre "grand cercle".
Ceci dit, c'est de la trigonométrie sphérique.
Je suppose que vous avez un formulaire, c'est pas difficile, seulement, il ne faut pas se tromper.
Pour un moment, oubliez l'expression "équation de ces deux courbes" et raisonnez en trigonométrie. Autrement dit, il suffit de résoudre les triangles sphériques. Mais, là j'ai déjà tout dit.

par **Anonyme** » 05 Mai 2013, 11:53

chan79 a écrit:Salut
Delta1 et Delta2 sont des cercles de centre O ?

Salut, bien vu chan.
Selon le sujet, Delta1 est en effet un cercle de centre O, mais Delta 2 ne l'est pas forcément.
D'ailleurs, dans le cas particulier où Delta2 en est un, il n'y alors que deux solutions au problème. Mais si Delta2 ne passe pas par A ou si Delta2 n'est pas orthogonal à Delta1, alors il y a une infinité de solutions (enfin je crois).
Mais ce qu'il faudrait c'est trouver les équations des deux courbes.

par **Anonyme** » 05 Mai 2013, 11:57

0liver a écrit:Salut, bien vu chan.
Selon le sujet, Delta1 est en effet un cercle de centre O, mais Delta 2 ne l'est pas forcément.
D'ailleurs, dans le cas particulier où Delta2 en est un, il n'y alors que deux solutions au problème. Mais si Delta2 ne passe pas par A ou si Delta2 n'est pas orthogonal à Delta1, alors il y a une infinité de solutions (enfin je crois).
Mais ce qu'il faudrait c'est trouver les équations des deux courbes.

J'ai dit des bêtises...
Je ne sais pas ce que c'est que la trigonométrie sphérique mais je vais creuser par là.
Je voyais en fait Delta2 comme une spirale "grimpant" sur la sphère, mais non c'est aussi un cercle en fait, mais pas forcément de centre O, si ?

par **Anonyme** » 05 Mai 2013, 12:06

0liver a écrit:J'ai dit des bêtises...
Je ne sais pas ce que c'est que la trigonométrie sphérique mais je vais creuser par là.
Je voyais en fait Delta2 comme une spirale "grimpant" sur la sphère, mais non c'est aussi un cercle en fait, mais pas forcément de centre O, si ?

En supposant que ce sont des cercles de centre O, la trigo sphérique résout tout le problème alors ?
Oui je ne sais pas ce que c'est parce que je suis en L2 physique, et j'avais envie de m'amuser un peu en étant curieux.

par **Dlzlogic** » 05 Mai 2013, 12:08

Bon, si on lit l'énoncé, il existe une infinité de courbes passant par A et B, comme il existe une infinité de chemins pour aller de Paris à Rome.
L'expression "points où se croisent" est assez surprenant aussi.
Pour mémoire, on appelle aussi le "grand cercle" la "géodésique".
Peut-être faudrait-il voir le contexte de cet exercice.

par **Anonyme** » 05 Mai 2013, 12:25

Bah en fait c'est un peu comme vous avez dis avec Paris et Rome.
En fait c'est une représentation de la Terre, dont on donne une longitude (Delta1) et deux autres points. Donc si on trace la géodésique (géodésique désigne la généralisation d'une ligne droite sur une surface, wikipédia) entre ces deux points (Delta2), elle va alors croiser Delta1 en plusieurs points. Et ce sont ces points qu'on cherche.
J'ai regardé la trigo sphérique, je vois un peu comment ça fonctionne mais, pas trop comment l'appliquer ici. Peut etre que c'est pas du tout de mon niveau encore.

par **Dlzlogic** » 05 Mai 2013, 13:00

Concernant le niveau et les compétences, ne vous en faites pas, moi je suis un incompétent sénile, alors vous ne devriez pas avoir de difficulté.
La trigo sphérique, ça se traite un peu comme la trigonométrie plane, sauf que les longueurs sont des arcs de grand cercle, donc on les exprime sous forme trigonométrique.
Je ne sais pas si votre exercice est en relation avec les coordonnées géographiques, en effet les conventions (origine et sens) ne sont pas les même que celles utilisées habituellement.
Deux grands cercles se coupent toujours en 2 points, diamétralement opposés.

Pour visualiser le problème imaginez les points C et D suffisamment proches, ce qui permet de dessiner sur une feuille de papier (plane) la figure.

par **Anonyme** » 05 Mai 2013, 15:02

Ok merci bien, je vais essayer de trouver des cours sur la trigo sphérique alors, et je vais faire brûler un peu de matière grise :)
Sinon, avec les équations des droites il n'y avait vraiment pas moyen de la faire ?

par **Dlzlogic** » 05 Mai 2013, 15:33

0liver a écrit:Ok merci bien, je vais essayer de trouver des cours sur la trigo sphérique alors, et je vais faire brûler un peu de matière grise
Sinon, avec les équations des droites il n'y avait vraiment pas moyen de la faire ?

A mon avis, les cours sur la trigo sphérique se limitent à un formulaire (j'ai tout ce qu'il faut) et une figure bien faite, vous en avez une.
La droite n'existe pas en géométrie sphérique, ce qui fait dire que la géométrie sphérique n'est pas Euclidienne, c'est vrai dans le mesure où la notion de droite n'existe pas et a fortiori, celle de parallèle, la somme des 3 angles d'un triangle ne vaut pas un angle plat, mais bon, c'est une question de terminologie.
Les problèmes liés à la forme de la terre sont autrement plus compliqués, la terre a la forme d'un ellipsoïde de révolution. Mais c'est une autre histoire.

par **Anonyme** » 05 Mai 2013, 16:18

Oui on simplifie la Terre par une boule sinon c'est sûr ça devient vachement compliqué.
Je pense avoir trouvé de bon cours, on trouve de tout sur internet ;) donc je vais potasser ça.
Merci à vous Dlzlogic de m'avoir aider.

par **leon1789** » 05 Mai 2013, 20:21

La notion de droite existe sur la sphère (et dans bien d'autres géométries) :id:
et le fait que, sur la sphère, la somme des angles d'un triangle ne soit pas 180° n'est pas une "question de terminologie" :mur: :mur:

par **leon1789** » 05 Mai 2013, 20:23

La notion de droite existe sur la sphère (et dans d'autres géométries non euclidiennes) :id:
et le fait que, sur la sphère, la somme des angles d'un triangle ne soit pas 180° n'est pas une "question de terminologie" :mur: :mur:

par **Anonyme** » 05 Mai 2013, 20:29

leon1789 a écrit:La notion de droite existe sur la sphère (et dans d'autres géométries non euclidiennes) :id:
et le fait que, sur la sphère, la somme des angles d'un triangle ne soit pas 180° n'est pas une "question de terminologie" :mur: :mur:

J'ai vu un contre exemple, et ça fait en effet pas 180° !

par **leon1789** » 05 Mai 2013, 20:56

0liver a écrit:J'ai vu un contre exemple, et ça fait en effet pas 180° !

oui bien sûr (on peut trouver facilement une exemple où la somme est 270° : un quart de la demi-sphère), et ce n'est donc une "question de terminologie". :zen:

par **Dlzlogic** » 05 Mai 2013, 21:40

Bon, tu sais Léon, on toujours trouver un terme ou une expression à critiquer dans une réponse de quelques lignes. Et, là t'es champion.
Olivier a posé une question concernant un exercice pas très précis ni très bien formulé. Mais après décodage, il n'y a plus d'ambiguïté.
Je voudrais bien que la modération m'explique la pertinence de cette intervention.
Si tu veux l'aider, tu y vas.
Si tu veux lui donner la solution, c'est ton problème.
En tout cas, je laisse tomber.

PS.
Avec Chan, nos messages se sont croisés, mais en gros on a eu la même réponse. Je suis sûr qu'on aurait exactement la même approche pour orienter Olivier. Je pose donc la question à la modération : quelle justification peut apport Léon concernant son intervention, sinon son entrainement, maintenant parfaitement au point, à la contestation systématique ?

par **LeJeu** » 06 Mai 2013, 07:59

0liver a écrit:Ok merci bien, je vais essayer de trouver des cours sur la trigo sphérique alors, et je vais faire brûler un peu de matière grise
Sinon, avec les équations des droites il n'y avait vraiment pas moyen de la faire ?

Bonjour,

Sauf erreur je n'ai pas l'impression que la trigo sphérique soit le plus cours chemin pour résoudre cet exo...

Je calculerais plutot l'équation du plan OCD
puis l'intersection avec le plan OAB ( y=0)

Le problème a été traité par Ben314 : ici

Le produit vectoriel semble donc un chapitre mieux adapté à ton pb :-)

par **Anonyme** » 06 Mai 2013, 10:20

LeJeu a écrit:Bonjour,

Sauf erreur je n'ai pas l'impression que la trigo sphérique soit le plus cours chemin pour résoudre cet exo...

Je calculerais plutot l'équation du plan OCD
puis l'intersection avec le plan OAB ( y=0)

Le problème a été traité par Ben314 : ici

Le produit vectoriel semble donc un chapitre mieux adapté à ton pb

Ah, oui, c'est bien aussi ça, les équations des plans, et c'est un peu ce dont je pensais avec les équations des courbes, mais là soit doit être bien plus simple.
Je crois qu'il faut que je trouve donc les équations des deux plans, puis les égaliser me donnera l'équation de la droite qui coupe ces deux plans, et ensuite en égalisant cette dernière avec l'équation de la sphère S, je devrais trouver les deux points.
C'est ça ?

par **Anonyme** » 06 Mai 2013, 10:32

oui c'est exactement ce qui est écrit dans l'autre sujet terminé. Donc ça devrait être bon maintenant.
Merci de votre aide.

Courbes en coordonnées sphériques

courbes en coordonnées sphériques

Qui est en ligne