Courbes en coordonnées sphériques

[chan79]

Bonjour,
Je calculerais plutot l'équation du plan OCD
puis l'intersection avec le plan OAB ( y=0)

Salut
La méthode de LeJeu me parait très bien.
Je mets un petit exemple.
Sur une sphère de centre O(0,0,0) et de rayon 9, on met les points:
A(0;0;9)
B(9;0;0)
C(1;4;8)
D(3;6;6)
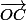
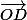
Le produit vectoriel de et est colinéaire au vecteur (4;-3;1).
Le plan OCD a comme équation 4x-3y+z=0
La droite intersection des plans OCD et OAB est définie par les deux équations:
4x-3y+z=0 et y=0
Pour trouver les coordonnées des deux points voulus, il faut résoudre le système à 3 équations:
x²+y²+z²=81
4x-3y+z=0
y=0
on obtient 17x²=81
puis les deux points et

[Anonyme]

Super, j'ai tout compris merci bien à vous tous. Et finalement c'était pas si compliqué que ça :)
Je pense que le poste peut être clos.
Encore merci à tous.

[leon1789]

Bon, tu sais Léon, on toujours trouver un terme ou une expression à critiquer dans une réponse de quelques lignes. Et, là t'es champion.
Olivier a posé une question concernant un exercice pas très précis ni très bien formulé. Mais après décodage, il n'y a plus d'ambiguïté.
Je voudrais bien que la modération m'explique la pertinence de cette intervention.
Si tu veux l'aider, tu y vas.
Si tu veux lui donner la solution, c'est ton problème.
En tout cas, je laisse tomber.

Presque amusant cette réaction épidermique.
Après nous avoir expliqué ici http://www.maths-forum.com/0-un-nombre-bien-genant-135330.php
que la géométrie sphérique est une géométrie euclidienne (c'est très étonnant de la part d'un géomètre), tu proclames maintenant qu'elle n'est pas euclidienne car il n'y existe pas de droites... Or la justification qu'elle n'est pas euclidienne vient d'ailleurs : tu devrais lire encore une fois la discussion citée ci-dessus (à partir du message de 11/12/2012, 17h22)

[LeJeu]

Presque amusant cette réaction épidermique.
Après nous avoir expliqué ici http://www.maths-forum.com/0-un-nombre-bien-genant-135330.php
que la géométrie sphérique est une géométrie euclidienne (c'est très étonnant de la part d'un géomètre), tu proclames maintenant qu'elle n'est pas euclidienne car il n'y existe pas de droites... Or la justification qu'elle n'est pas euclidienne vient d'ailleurs : tu devrais lire encore une fois la discussion citée ci-dessus (à partir du message de 11/12/2012, 17h22)

Leon, bonsoir

C'est bien de noter les erreurs de Dlzlogic, mais tu pourrais remarquer qu'il a bien retenu que la géométrie sphérique n'est pas euclidienne ....

Sinon, pourquoi ne pas encourager Oliver, et féliciter Chan79 pour sa contribution :

Restons positifs , ( quelles que soient les erreurs passées !)

[Sylviel]

Je pose donc la question à la modération : quelle justification peut apport Léon concernant son intervention, sinon son entrainement, maintenant parfaitement au point, à la contestation systématique ?

Léon critique peut-être facilement tes interventions mais celle-ci n'est pas injustifiée:
tu fais deux affirmations qui sont mathématiquement fausses :
1) le fait qu'il n'y a pas de droites en géométrie sphérique
2) le fait que la somme des angles ne valent pas 180° soit une simple question de terminologie (encore que cette phrase soit suffisamment fourre tout pourqu'on lui trouve une explication)

et ils les corrigent pour éviter à un étudiant d'être induit en erreur.

De fait vous avez tout deux des réactions très violentes l'un vis à vis de l'autre. Ici je ne pense pas que son message mérite une quelconque modération, pas plus que les tiens.