Equation de plan

par **Haki** » 05 Déc 2011, 19:17

Bonjour, comment trouver une équation du plan (ABC) avec A(2;4;3), B(4;-2;3), C(1;-1;1) ?

par **el niala** » 05 Déc 2011, 19:33

tu cherches les coordonnées d'un vecteur normal au plan (si tu connais le produit vectoriel c'est immédiat puisque

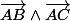
en est un)

et tu exprimes que le produit scalaire de ce vecteur avec

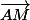
est nul

par **Haki** » 05 Déc 2011, 19:41

Je ne vois pas comment on trouve un vecteur normal :S

par **el niala** » 05 Déc 2011, 19:44

donc apparemment tu ne connais pas le produit vectoriel
soit

ce vecteur

pour être normal au plan, il faut et il suffit qu'il soit orthogonal à 2 vecteurs non colinéaires de ce plan, tu ne vois pas quels pourraient être ces 2 vecteurs par exemple ?

par **Haki** » 05 Déc 2011, 19:56

ce que j'ai fait :

soit le vecteur n(a;b;c) un vecteur normal au plan (ABC).

J'ai calculé AB.n=0 et trouvé 2a-6b=0
Puis AC.n=0 me donne -a-5b-2c=0

Il faudrait donc faire un systeme, seulement je ne sais pas le résoudre, c'est un systeme qui a 3inconnues mais seulement 2 équations ..

par **el niala** » 05 Déc 2011, 20:04

Haki a écrit:ce que j'ai fait :

soit le vecteur n(a;b;c) un vecteur normal au plan (ABC).

J'ai calculé AB.n=0 et trouvé 2a-6b=0
Puis AC.n=0 me donne -a-5b-2c=0

Il faudrait donc faire un systeme, seulement je ne sais pas le résoudre, c'est un systeme qui a 3inconnues mais seulement 2 équations ..

c'est normal (si j'ose :zen: ) il n'existe pas qu'un seul vecteur normal au plan, tu vas obtenir b et c en fonction de a par exemple, choisis alors a=ce qui te plait de manière à obtenir des valeurs simples

par **Haki** » 05 Déc 2011, 20:13

d'accord donc ce que j'ai fait c'est juste? Il ne me reste qu'a donner une valeur à a ?

par **el niala** » 05 Déc 2011, 20:32

OK pour tes calculs, a=3 me paraît judicieux :lol3:

par **Haki** » 05 Déc 2011, 20:38

Ok merci beaucoup !

par **sad13** » 06 Déc 2011, 12:57

Que représente M , un point du plan tel que le vecteur AM soit normal?

par **Haki** » 06 Déc 2011, 13:29

comment M peut il etre dans le plan si AM est un vecteur normal a ce plan .. ?

par **sad13** » 06 Déc 2011, 14:38

je questionnais niala mais il est dans le plan orthogonal au plan considéré

par **Haki** » 06 Déc 2011, 14:56

et alors .. ? la méthode qu'il a proposé n'est pas correcte ?

par **sad13** » 06 Déc 2011, 14:57

mais biensûr qu'elle est correcte, bon j'ai rien dit, dsl de t'avoir perturbé

par **el niala** » 06 Déc 2011, 16:29

@ sad13

la lettre M est couramment utilisée pour désigner un point quelconque de quelque chose, ici M(x,y,z) est un point quelconque du plan dont on cherche à déterminer l'équation cartésienne

Equation de plan

equation de plan

Qui est en ligne