Bonjour j'aurais besoin d'aide pour un DM de maths sur les suites a rendre pour demain!
J'ai eu 0/20 a mon premier controle de maths et il faut vraiment que je rattrappe cette note car je suis en S et en plus je fais spé maths :s
Donc l'aide la plus rapide serait la bienvenue :)
Ex1)
On considère la suite (Un), nN, définie par U0=5 et, pour tout entier n>1 (le signe c'est plus grand ou égal):
Un=(1+ 2/n )Un-1 + 6/n
1.a. Calculer U1
b. Les valeurs de U2, U3, U4, U5, U6, U7, U8, U9, U10, U11 sont respectivement égales à :
45, 77, 117, 165, 221, 285, 357, 437, 525, 621
A partir de ces données, conjecturer la nature de la suite (dn), nN, définie par dn = Un+1 - Un
2. On considère la suite arithmétique (Vn), nN, de raison 8 et de premier terme v0=16
Justifier que la somme des n premiers termes de cette suite est égale à 4n^2 + 12n
3. Démontrer par récurrence que pour tout entier naturel n on a :
Un=4n^2 + 12n + 5
4. Valider la conjecture émise à la question 1.b.
Voilà j'espère avoir été clair, il y a un deuxième exercice que je vais taper dans 5min.
Merci d'avance pour votre aide ;)
Aide DM Suites Terminale S
12 messages
- Page 1 sur 1
Nono182 a écrit:Bonjour j'aurais besoin d'aide pour un DM de maths sur les suites a rendre pour demain!
J'ai eu 0/20 a mon premier controle de maths et il faut vraiment que je rattrappe cette note car je suis en S et en plus je fais spé maths :s
Donc l'aide la plus rapide serait la bienvenue
Pas de découragement !
Nono182 a écrit:Ex1)
On considère la suite (Un), nN, définie par U0=5 et, pour tout entier n>1 (le signe c'est plus grand ou égal):
Un=(1+ 2/n )Un-1 + 6/n (1)
la formule (1) est une formule de récurrence. Les termes sont numérotés.
dès que l'on connait celui de numéro n-1 (on dit "d'indice (n-1)"
on calcule le suivant d'indice n
Nono182 a écrit:
A partir de ces données, conjecturer la nature de la suite (dn), nN, définie par dn = Un+1 - Un
On voit que les différences forment une progression arithmétique
On va donc calculer leur somme , de deux façons:
(1) avec la formule d'une somme de termes de progression arithmétique
(2) par télécopie, car chaque terme étant une différence,
au final la somme se simplifie , il reste "le dernier " diminué du "premier"
Nono182 a écrit:
2. On considère la suite arithmétique (Vn), nN, de raison 8 et de premier terme v0=16
Justifier que la somme des n premiers termes de cette suite est égale à 4n^2 + 12n
Comme ils donnent la formule, il suffit de la montrer par récurrence.
A chaque étape, on rajoute le terme arithmétique
qui a pour expression
Nono182 a écrit:3. Démontrer par récurrence que pour tout entier naturel n on a :
Un=4n^2 + 12n + 5
Comme la formule de récurrence et son 1er terme définissent la suite,
tu peux p-e montrer que le polynome
formule de récurrence ...
mathelot a écrit:On va donc calculer leur somme , de deux façons:
(1) avec la formule d'une somme de termes de progression arithmétique
(2) par télécopie, car chaque terme étant une différence,
au final la somme se simplifie , il reste "le dernier " diminué du "premier"
Par télécopie? j'ai pas encore appris ca ^^ca lfait pas trop si jle met dans ma copie apres mon 0 x)
La question (2) est un grand classique...
ce genre de suite s'appelle arithmético-géométrique
c'est un mix (hybride) de suite arithmétique et géométrique
l'idée c'est de calculer la valeur du point fixe
si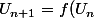)
on écrit l'équation
x=f(x)
la solution l est "point fixe"
en soustrayant au terme général u_n, la suite devient géométrique
au terme général u_n, la suite devient géométrique
ce genre de suite s'appelle arithmético-géométrique
c'est un mix (hybride) de suite arithmétique et géométrique
l'idée c'est de calculer la valeur du point fixe
si
on écrit l'équation
x=f(x)
la solution l est "point fixe"
en soustrayant
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

