Intégrale curviligne complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 12 Jan 2014, 14:26
par Supernova » 12 Jan 2014, 14:26
Hello Forum

On cherche à calculer l'intégrale:

Où

est le contour défini par le segment

et le demi cercle situé dans le demi plan supérieur de diamètre le segment

avec

En fait, je sais pas quelle technique utiliser, j'ai essayé d'utiliser le Th de CAUCHY, ou d'écrire une fois

et une autre fois

sous forme d'une série mais sans succès :/
Aurriez-vous donc lobligeance de m'aider !
Merci
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 12 Jan 2014, 15:58
par Maxmau » 12 Jan 2014, 15:58
Supernova a écrit:Hello Forum

On cherche à calculer l'intégrale:

Où

est le contour défini par le segment

et le demi cercle situé dans le demi plan supérieur de diamètre le segment

avec

En fait, je sais pas quelle technique utiliser, j'ai essayé d'utiliser le Th de CAUCHY, ou d'écrire une fois

et une autre fois

sous forme d'une série mais sans succès :/
Aurriez-vous donc lobligeance de m'aider !
Merci
Bj
formule des résidus peut être ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 12 Jan 2014, 20:11
par Pythales » 12 Jan 2014, 20:11
Supernova a écrit:Hello Forum

On cherche à calculer l'intégrale:

Où

est le contour défini par le segment

et le demi cercle situé dans le demi plan supérieur de diamètre le segment

avec

En fait, je sais pas quelle technique utiliser, j'ai essayé d'utiliser le Th de CAUCHY, ou d'écrire une fois

et une autre fois

sous forme d'une série mais sans succès :/
Aurriez-vous donc lobligeance de m'aider !
Merci
Il faut effectivement utiliser le théorème de Cauchy.
Le seul point singulier dans le domaine limité par le contour est
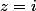
de résidu
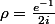
et ton intégrale vaur

-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 13 Jan 2014, 12:37
par deltab » 13 Jan 2014, 12:37
Bonjour.
Je pense qu'ici qu'il est demandé d'utiliser le théorème de Cauchy (formule intégrale) en écrivant
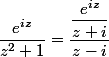
et à ce niveau il est prématuré de parlé de résidu.
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 13 Jan 2014, 20:51
par Supernova » 13 Jan 2014, 20:51
comme ça on aura deux termes, celui qui contient ( z + i ) en dénominateur sera nul car -i n'est pas à l'intérieur du contour ? l'autre terme nous donnera pi/e
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 14 Jan 2014, 07:18
par deltab » 14 Jan 2014, 07:18
Bonjour.
Oui
Supernova a écrit:comme ça on aura deux termes, celui qui contient ( z + i ) en dénominateur sera nul car -i n'est pas à l'intérieur du contour ? l'autre terme nous donnera pi/e
Ceci en écrivant
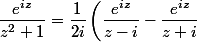)
Pour le calcul, je me référais à l'application directe de formule intégrale de Cauchy
=\dfrac{1}{2\pi i}\int_\Gamma \dfrac{f(z)}{z-z_0} dz)
, avec
=\dfrac{e^{iz}}{z+i})
et
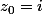
.
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 14 Jan 2014, 15:40
par Supernova » 14 Jan 2014, 15:40
deltab a écrit:Bonjour.
Oui
Ceci en écrivant
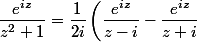)
Pour le calcul, je me référais à l'application directe de formule intégrale de Cauchy
=\dfrac{1}{2\pi i}\int_\Gamma \dfrac{f(z)}{z-z_0} dz)
, avec
=\dfrac{e^{iz}}{z+i})
et
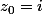
.
Exactement! J'ai procédé ainsi

Merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
est le contour défini par le segment
et le demi cercle situé dans le demi plan supérieur de diamètre le segment
avec

et une autre fois
sous forme d'une série mais sans succès :/
est le contour défini par le segment
et le demi cercle situé dans le demi plan supérieur de diamètre le segment
avec

et une autre fois
sous forme d'une série mais sans succès :/