Bonjour, je suis en licence et je n'arrive pas a calculer les intégrales multiples, voir certaines intégrales simples, quand les bornes sont l'infini
Par exemple : ;);) ;);) exp(-(x²+2xy+3y²))dx dy,
Merci de votre aide
Aide pour une intégrale
9 messages
- Page 1 sur 1
sylvain41 a écrit:Bonjour, je suis en licence et je n'arrive pas a calculer les intégrales multiples, voir certaines intégrales simples, quand les bornes sont l'infini
Par exemple :;)
;) exp(-(x²+2xy+3y²))dx dy,
Merci de votre aide
êtes vous sur (x²+2xy+3y²) ??? je pense plutôt (x²/3+2xy+3y²) = ( x/rac(3)+ y .rac(3) )²
ce qui donne
Dans ce cas, l'intégrale surmorpho a écrit:êtes vous sur (x²+2xy+3y²) ??? je pense plutôt (x²/3+2xy+3y²) = ( x/rac(3)+ y .rac(3) )²
ce qui donneexp(-t²) dt on sait calculer ......
Il suffit de mettre l'exposant sous forme "canonique" :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonjour.
Pour cet exercice, il est aisé de le faire si l'on à déjà vu la méthode de calcul de par passage à une intégrale double. Sinon les allusions à cette méthode seront incompréhensibles. Le lecteur au courant de cette méthode a juste besoin qu'on le mette dans la voie, il fera alors de lui_même les calculs nécessaires.
par passage à une intégrale double. Sinon les allusions à cette méthode seront incompréhensibles. Le lecteur au courant de cette méthode a juste besoin qu'on le mette dans la voie, il fera alors de lui_même les calculs nécessaires.
sylvain41
As-tu vu cette méthode?
Pour cet exercice, il est aisé de le faire si l'on à déjà vu la méthode de calcul de
sylvain41
As-tu vu cette méthode?
Euhhhh.... je voudrais bien voir comment tu fait un changemnt de variable qui, partant d'une intégrale double donne comme résultat une intégrale simple :morpho a écrit:==> je ne calcule pas sur R² vu que c'est dt !!!!
Si tu pose uniquement
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Euhhhh.... je voudrais bien voir comment tu fait un changemnt de variable qui, partant d'une intégrale double donne comme résultat une intégrale simple :
Si tu pose uniquement, comment tu trouve x en fonction de t (et donc dx en fonction de dt) ?
On s'est mal compris !!! du moins j'ai mal expliqué. Je voudrais simplement dire que si on sait calculer
Si on ne connait pas I alors on se débrouille en passant par les coor polaire ça aide ....
Bonjour
On a:
 (la varible d'intégration est muette) d'où:
(la varible d'intégration est muette) d'où:
^2=\int_0^\infty e^{-u^2}du \times\int_0^\infty e^{-v^2}dv=\iint_D e^{-(u^2+v^2)}dudv.) où D=[0,+\infty[ \times [0,+\infty[.
où D=[0,+\infty[ \times [0,+\infty[.
Le passage en coordonnées polaires,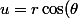) ,
, 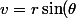 ), dans la dernière intégrale (intégrale double) donne:
), dans la dernière intégrale (intégrale double) donne:
}dudv=\int_0^{\pi/2}\left(\int_0^\infty re^{-r^2}dr \right)d\theta=\dfrac{\pi}{2} \times \left. \dfrac{-e^{-r^2}}{2}\right|_0^\infty =\dfrac{\pi}{4})
[
morpho a écrit:On s'est mal compris !!! du moins j'ai mal expliqué. Je voudrais simplement dire que si on sait calculer, on peut s'en sortir.
Si on ne connait pas I alors on se débrouille en passant par les coor polaire ça aide ....
On a:
Le passage en coordonnées polaires,
[
deltab a écrit:Bonjour
On a:(la varible d'intégration est muette) d'où:
où D=[0,+\infty[ \times [0,+\infty[.
Le passage en coordonnées polaires,,
), dans la dernière intégrale (intégrale double) donne:
Justifier le choix du domaine avant le changement de variable pour que les intégrales existent ( parité )
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
