Aide pour une intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jesi
- Messages: 1
- Enregistré le: 29 Aoû 2017, 08:31
-
par jesi » 29 Aoû 2017, 08:48
Bonjour,
Pourriez-vous m'aider à calculer cette intégrale. Je reste bloqué au niveau de la primitive. Je pense que je dois faire un changement de variable mais vu la complexité de l'équation je ne sais pas par où commencer :
- int.jpg (25.54 Kio) Vu 273 fois
La réponse :
- int2.jpg (8.71 Kio) Vu 273 fois
-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
par chan79 » 29 Aoû 2017, 09:18
salut
Décompose en éléments simples
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 29 Aoû 2017, 09:32
salut
quelle écriture peu esthétique (ni même efficace) de l'intégrale ...
posons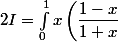
^2 dx)
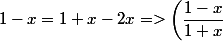^2 = 1 - 4 \dfrac {x {\blue + 1 - 1}} {1 + x} + \dfrac {4(x {\blue + 1 - 1})^2} {(1 + x)^2} =)
^2} = ...)
il suffit de simplifier et de multiplier par x ... puis de simplifier à nouveau (réduction en éléments simples) et une primitive est alors évidente ...
encore plus simple :
^2 = (x - 1)^2)
donc
^2 = 1 - \dfrac 4 {x + 1} + \dfrac 4 {(x + 1)^2})
il suffit de multiplier par x et de regarder ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
par aymanemaysae » 29 Aoû 2017, 12:56
Bonjour ;
En posant
on a :
^2 = (y-1)(\dfrac{y-2}{y})^2 = (y-1)(1-\dfrac{2}{y})^2)
(1- \dfrac{4}{y}+\dfrac{4}{y^2}) = y - 1 + 4 \dfrac{y-1}{y^2} - 4 \dfrac{y-1}{y})
- 4(1 - \dfrac{1}{y}) = y - 5 + \dfrac{8}{y}-\dfrac{4}{y^2} .)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
