jonses a écrit:Bonjour ou bonsoir,
Je suis sur un exercice que je n'arrive pas à résoudre (en plus c'est sur les fonctions, le domaine où j'ai vraiment du mal), si quelqu'un pourrait me donner une petite piste svp :
Soit f une fonction continue de R dans R telle que :

.
Je dois montrer que f admet un minimum.
J'ai essayé de raisonner par l'absurde en supposant que f n'est pas minorée puis essayer avec le théorème des valeurs intermédiaires d'aboutir sur une contradiction (ensuite je me démerderais pour montrer que la borne inf est un minimum), mais en vain.
J'ai tenté de passer par l'étude d'un point a quelconque de R et de son image f(a) en m'intéressant à l'intervalle
,+\infty[)
, mais ça me mène nulle part. Et maintenant je bloque totalement
Merci d'avance pour vos réponses
Ton idée d'intervalle est interessante, mais pourquoi le f(a)?
On prend un intervalle quelconque de la forme
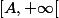
et on utilise les hypothèses.
 =+\infty)
: il existe a tel que x A
 =+\infty)
: il existe b tel que x> b entraine f(x) > A
Tu montres que la fonction est minorée sur l'intervalle [a;b] et comme elle est minorée sur son complémentaire, tu en déduiras que f est minorée puis tu conclues.
Correctif:Tu as raison, il faut choisir A sous la forme f(x0) pour rendre la conclusion facile car la borne inf est soit dans l'image de [a , b], soit dans
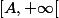
. Si elle est dans [a,b] tu utilises la compacité pour conclure et si elle est dans
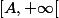
, c'est A qui est bien un minimum.
