Linéarisation

[Raphoul]

je suis bon jusqu'à la ? j'ai pas fais d'erreur ?

ah oui le moins

[leon1789]

ok.
Ensuite, il revient des cosinus

Bye :dodo: :dodo:

[Raphoul]

i² = -1 !!!
donc (2i)² = -4




-

ok. Ensuite?

ensuite
on a du

[Raphoul]

? peut être une erreur de signe

[Raphoul]

c'est juste ou pas ce résultat ?

[leon1789]

oui, il est correct.

Maintenant, il faut l' intégrer entre 0 et Pi / 4

[Raphoul]

oui, il est correct.

Maintenant, il faut l' intégrer entre 0 et Pi / 4

le résultat simplifier est :

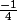
il faut que je trouve une primitive, pour pas de problème par contre pour les autre termes je ne vois pas trop

[leon1789]

Ok, dans ce cas une indication : quelles sont les dérivées des fonctions suivantes ?
x -> sin(x)
x -> cos(x)
x -> a.sin(x)
x -> a.cos(x)
x -> sin(b.x)
x -> cos(b.x)

où a,b sont des réels.

[Raphoul]

Ok, dans ce cas une indication : quelles sont les dérivées des fonctions suivantes ?
x -> sin(x)
x -> cos(x)
x -> a.sin(x)
x -> a.cos(x)
x -> sin(b.x)
x -> cos(b.x)

où a,b sont des réels.

x' -> cos(x)
x' -> -sin(x)
x' -> a.cos(x)
x' -> -a.sin(x)
x' -> b.cos(b.x)
x' -> -b.sin(b.x)

[leon1789]

x' -> cos(x)
x' -> -sin(x)
x' -> a.cos(x)
x' -> -a.sin(x)
x' -> b.cos(b.x)
x' -> -b.sin(b.x)

ok, c'est simple, mais il faut le savoir pour intégrer


Now, est-ce tu peux intégrer les fonctions suivantes ?
x -> cos(x)
x -> a.cos(x)
x -> b.cos(b.x)
x -> cos(b.x)
x -> a.cos(b.x)

[Raphoul]

ok, c'est simple, mais il faut le savoir pour intégrer


Now, est-ce tu peux intégrer les fonctions suivantes ?
x -> cos(x)
x -> a.cos(x)
x -> b.cos(b.x)
x -> cos(b.x)
x -> a.cos(b.x)

X -> sin(x)
X -> a.sin(x)
X -> sin(b.x)
X ->
X ->

[leon1789]

X -> sin(x)
X -> a.sin(x)
X -> sin(b.x)
X ->
X ->

Yes, that's it !

Maintenant, tu intrègres sans souci :
x -> -1/4
x -> 1/2 Cos(2*x)
x -> 1/4 Cos(4*x)
x -> -1/4 + 1/2 Cos(2*x) - 1/4 Cos(4*x)

[Raphoul]

Yes, that's it !

Maintenant, tu intrègres sans souci :
x -> -1/4
x -> 1/2 Cos(2*x)
x -> 1/4 Cos(4*x)
x -> -1/4 + 1/2 Cos(2*x) - 1/4 Cos(4*x)

oui je trouve après simplification :

[Raphoul]

oui je trouve après simplification :

c'est bon je trouve le résultat recherché, merci beaucoup

[Raphoul]

quelqu'un peut voire vite fais mon 2eme petit soucis posté dans le premier message ?

[leon1789]

au numérateur ca fait :

mais au dénominateur je ne vois pas

Au dénominateur, il y a du sinus. (je n'ai pas vérifié tes calculs de z).

[Raphoul]

Au dénominateur, c'est un sinus ? (je n'ai pas vérifié tes calculs de z).

c'est pas sa la formule d'Euler pour un sinus

[leon1789]

c'est pas sa la formule d'Euler pour un sinus

ben si :zen: avec l'angle ...

[Raphoul]

ben si :zen: avec l'angle ...

ah oui c'est vrai ça marche

[Raphoul]

je n'avais pas reconnu la formule avec le moins