Prépa hec exercice quantificateurs

par **nanou213** » 05 Sep 2006, 20:12

(re) bonsoir :p

je travaille les quantificateurs :)

pour dire qu'une fonction est continue aux abords d'un point A :

quelque soit epsilone positif ;(il existe) alpha positif, quelque soit x, |x-a|
mais comment exprimer f non continue au point a ?
Sur quel parametre jouer?

par **nuage** » 05 Sep 2006, 21:24

Salut.
La négation de

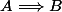
est

.
La négation de

est

.
La négation de

est

Dire que la fonction f n'est pas continue en a s'écrit donc :

par **nada-top** » 06 Sep 2006, 08:26

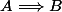
nuage a écrit:La négation de est .

on a

..en tous c'est ce que tu as appliqué .

@+

par **nox** » 06 Sep 2006, 08:46

ce qu'avait dit nuage était bon...inférieur ou inférieur ou égal je crois que peu importe...

par **nox** » 06 Sep 2006, 08:47

je pense que inférieur ou inférieur ou égal peu importe...du moment que c'est cohérent avec la définition de la continuité

par **nada-top** » 06 Sep 2006, 08:55

tu veux dire que :

et

c'est la meme chose ?!
car supposons qu'il a fait la négation de :

Edit: oui c cohérent avec la définition de continuité mais c'est un exo de logique ça donc il faut appliquer toutes les régles de la négation.
enfin il se peut que je me trompe .

par **nox** » 06 Sep 2006, 08:57

nada-top a écrit:tu veux dire que : et c'est la meme chose ?!

ah non!!!évidemment!!!
mais dans la définition de la continuité cette partie n'est pas euh..."négativée" ^^

nada-top a écrit:car supposons qu'il a fait la négation de :

wai
c'est ce qu'il a fait

nada-top a écrit:Edit: oui c cohérent avec la définition de continuité mais c'est un exo de logique ça donc il faut appliquer toutes les régles de la négation.
enfin il se peut que je me trompe .

quand on fait la négation on ne touche pas à cette inégalité...d'ailleurs dans la version que tu proposes tu ne changes pas le sens non plus. Donc on est d'accord...c'est juste que tu avais l'air de dire que la réponse de nuage était fausse à cause de l'inférieur strict...en tout cas c'est comme ca que je l'ai compris...

par **nada-top** » 06 Sep 2006, 09:03

nox a écrit:mais dans la définition de la continuité cette partie n'est pas euh..."négativée" ^^

quelle partie ?

par **nox** » 06 Sep 2006, 09:04

cella la..mais la tu es d'accord tu ne l'as pas "négativée" non plus...

par **nox** » 06 Sep 2006, 09:05

je crois que depuis le début on est d'accord en fait :ptdr:

simplement on parle pas de la meme chose

moi ce qui m'a fait réagir c'est ca :

nada-top a écrit:(c'est ce qu'a fait nuage mais on a

par **nada-top** » 06 Sep 2006, 09:13

on est don d'accord : j'ai pas fait la négation de cette partie :we:
voilà tout le problème moi j'ai fait la négation de :

et ça donne :

et apparemment nuage a fait la négation de :

si tu remarque lui a écrit (

) tandis que

Edit : ''je crois que depuis le début on est d'accord en fait :ptdr:'' et oui c'est ça .

par **nox** » 06 Sep 2006, 09:15

waip on est donc totalement d'accord... :we:

une bonne dizaine de posts pour rien dire donc :ptdr:

par **nox** » 06 Sep 2006, 09:21

j'ai tout viré on était d'accord et on parlait dans le vide :ptdr:

Prépa hec exercice quantificateurs

prépa hec exercice quantificateurs

Qui est en ligne