Bonsoir, je coince un petit peu sur cet exercice.
En bref, on me donne une fonction f(x)=ln(sqrt(1+x^2)-x)/ln(1+sqrt(2))
et on définit la suite (u indice n+1) = f(un)
On m'a demandé d'étudier le signe de f(x)+x, puis de montrer que les suites (u indice 2n) et (u indice 2n+1) étaient monotones. Jusque là c'est ok.
Mais après, on me demande de démontrer que, si u0 est strictement compris entre 0 et 1, la suite u possède deux valeurs d'adhérence, -1 et +1.
Puis on me demande, que dire de la suite u lorsque u0 est strictement supérieur à 1 ?
Je ne vois pas trop, je comptais étudier la fonction g=fof mais cela n'aboutit pas.
Merci d'avance de vos conseils.
Bonne soirée.
Valeurs d'adhérence d'une suite.
2 messages
- Page 1 sur 1
En dérivant  on obtient :
on obtient :=-\frac{1}{\ln(1+\sqrt{2})\sqrt{1+x^2})}0) et
et 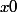 , alors
, alors  est croissante.
est croissante.
Si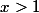 alors
alors |-|f(f(x))|=-f(x)-f(f(x))=-(f(x)+f(f(x)))) , on peut concluire que
, on peut concluire que +(f\circ f)'(x))=-f'(x)(f'(f(x))+1)>0) (vérifier que
(vérifier que >-1) si
si  ), et comme
), et comme -f(f(0))=0) , on a que
, on a que |-|f(f(x))|0) si
si 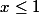 . Alors si tu prennes
. Alors si tu prennes  , alors la suite
, alors la suite _{n\geq 1}) est borné par
est borné par  , alors cette suite est monotone et bornée alors celle-ci a un limite L. Remaque que
, alors cette suite est monotone et bornée alors celle-ci a un limite L. Remaque que |=|u_{n+1}|) , si tu prennes le limite tu auras que
, si tu prennes le limite tu auras que |=L) , comme
, comme  alors
alors =L) , il faut déterminer
, il faut déterminer  et tu pourras déterminer les valeurs d'adhérence.
et tu pourras déterminer les valeurs d'adhérence.
J'espère ne pas avoir fait un erreur de calcul. À bientót
Si
J'espère ne pas avoir fait un erreur de calcul. À bientót
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
