Dérivé du logarithme népérien

[nicolas2]

Bonjour, arrivant à la partie B de mon exercice je bloque. On a la fonction b(x)= et l'on me demande de prouvé que b'(x)=

Je ne comprends pas vraiment d'ou vient le 3,5 ... et comment la dérivé de 2x X ln(x) devient 2ln(x) ... pouvez m'expliquer svp

[nicolas2]

Bonjour, arrivant à la partie B de mon exercice je bloque. On a la fonction b(x)= et l'on me demande de prouvé que b'(x)=

Je ne comprends pas vraiment d'ou vient le 3,5 ... et comment la dérivé de 2x X ln(x) devient 2ln(x) ... pouvez m'expliquer svp

Cela voudrait alors dire que la dérivé de ln(x) est ln(x) ... mais je ne comprends toujours pas le 3,5

[chombier]

Cela voudrait alors dire que la dérivé de ln(x) est ln(x) ... mais je ne comprends toujours pas le 3,5

Quelle est la dérivée de ?

[WillyCagnes]

Cela voudrait alors dire que la dérivé de ln(x) est ln(x) ... mais je ne comprends toujours pas le 3,5

Merci pour ton Bonjour....

revise ton cours , la dérivée de ln(x)= 1/x

et recommence ta dérivée

[nicolas2]

Quelle est la dérivée de ?

En appliquant cette formule je tombe sur b'(x)= c'est n'est pas ce qui est donné dans l'énnoncé de l'exercice ..

[chombier]

En appliquant cette formule je tombe sur b'(x)= c'est n'est pas ce qui est donné dans l'énnoncé de l'exercice ..

Détaille la façon dont tu dérives, et on te dira où est ton erreur

[nicolas2]

Quelle est la dérivée de ?

Je ne comprends pas très bien .. :/

[nicolas2]

Je ne comprends pas très bien .. :/

alors je fais :


=

[nicolas2]

alors je fais :


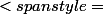
=1,5-2x+(2/x)"/>

Voilà la correction

[chombier]

Je ne comprends pas comment tu dérives





avec u(x) = 2x et v(x) = ln(x)



Continues...

[nicolas2]

Je ne comprends pas comment tu dérives





avec u(x) = 2x et v(x) = ln(x)



Continues...

Cette formule est-elle juste : (ln(x))'= x'/x ?
Si oui voilà la suite :

=

[chombier]

Cette formule est-elle juste : (ln(x))'= x'/x ?
Si oui voilà la suite :

=

Non.
Pourquoi as-tu dérivé la deuxième occurrence de ?

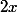
[nicolas2]

Non.
Pourquoi as-tu dérivé la deuxième occurrence de ?

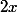
Je ne comprends pas très bien, j'ai appliqué les formules que tu m'as donné

[nicolas2]

Je ne comprends pas très bien, j'ai appliqué les formules que tu m'as donné

A quoi est égale ln(x) ' ?

[chombier]

Je ne comprends pas très bien, j'ai appliqué les formules que tu m'as donné

Ben non. Tu as mal dérivé dans

C'est le produit de 2x et de la dérivée de ln(x)

[chombier]

A quoi est égale ln(x) ' ?

à 1/x. Tu as un cours, non ? Avant de faire ses exercices, on relit son cours...

[nicolas2]

Ben non. Tu as mal dérivé dans

C'est le produit de 2x et de la dérivée de ln(x)

Le truc c'est que ne comprends pas qu'elle est la dérivé de

[nicolas2]

à 1/x. Tu as un cours, non ? Avant de faire ses exercices, on relit son cours...

Crois que moi que je n'ai jamais fais lma dérivé de ln dans mon cours ...

Et vu ln(x)' = 1/x je ne comprends pas mon erreur, car 2(1/x) = 2/x non ?

[chombier]

Crois que moi que je n'ai jamais fait la dérivée de ln dans mon cours ...

Et vu ln(x)' = 1/x je ne comprends pas mon erreur, car 2(1/x) = 2/x non ?

Bien sur, bien sur...

Bon allez, on reprends tous en cœur :

[nicolas2]

Bien sur, bien sur...

Bon allez, on reprends tous en cœur :

Pourquoi dis-tu ca alors que tu ne connais même pas mon cours ? La seule formule que j'ai faite est est que =


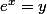
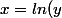Merci, je viens de comprendre mon erreur. J'ai dérivé (2x) alors qu'il ne fallaitpas , ainsi on arrive sur 2x/x, il reste 2 qui explique le 3,5 que je ne comprenais pas ... Merci de l'aide