Théorie des ensembles
22 messages
- Page 1 sur 2 - 1, 2
Théorie des ensembles
Bonjour,
Un énoncé d'exercice en théorie des ensembles est le suivant:
Soit E l' ensemble des entiers naturels inférieurs à 10,
soit A={1,4,8,6,2}
et la question la suivante:
Quel est le complémentaire de A dans E?
Je vous demande de l'aide car je ne comprends pas le corrigé, merci d'avance...
Un énoncé d'exercice en théorie des ensembles est le suivant:
Soit E l' ensemble des entiers naturels inférieurs à 10,
soit A={1,4,8,6,2}
et la question la suivante:
Quel est le complémentaire de A dans E?
Je vous demande de l'aide car je ne comprends pas le corrigé, merci d'avance...
Salut !
Salut, en notant) , l'ensemble complémentaire de
, l'ensemble complémentaire de  dans
dans  , par définition :
, par définition :
) est l'ensemble des éléments de
est l'ensemble des éléments de  privés de ceux de
privés de ceux de  ou encore :
ou encore :
=E\setminus A=\{x\in E|x\notin A\}) .
.
Remarques qui peuvent te servir pour voir si ce que tu dis paraît bon : Pour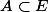 :
:
1°/ = E)
2°/=\empty)
3°/\) =A)
keyz a écrit:Bonjour,
Un énoncé d'exercice en théorie des ensembles est le suivant:
Soit E l' ensemble des entiers naturels inférieurs à 10,
soit A={1,4,8,6,2}
et la question la suivante:
Quel est le complémentaire de A dans E?
Je vous demande de l'aide car je ne comprends pas le corrigé, merci d'avance...
Salut, en notant
Remarques qui peuvent te servir pour voir si ce que tu dis paraît bon : Pour
1°/
2°/
3°/
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
keyz a écrit:Bonjour,
Un énoncé d'exercice en théorie des ensembles est le suivant:
Soit E l' ensemble des entiers naturels inférieurs à 10,
soit A={1,4,8,6,2}
et la question la suivante:
Quel est le complémentaire de A dans E?
Je vous demande de l'aide car je ne comprends pas le corrigé, merci d'avance...
Sans plus grande précision, "inférieur" signifie "
keyz a écrit:Merci pour votre post capitaine nuggets
Je voudrais comparer la réponse; car j'emets un doute quant à celle du livre...
Alors pour moi, le complémentaire de A dans E est {0,3,5,7,9}, est-ce bien cela?
Du coup,
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
De rien :++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Bonjour,
C'est officiel ?
Donc, si on dit "inférieur ou égal" c'est la même chose que "inférieur", donc "égal" est superflu, inutile parce que sous-entendu ?
Cette interprétation peut se justifier sans le cas des réels, mais j'aimerais bien confirmation dans le cas des entiers.
PS. Et pour être complet dans ma question si je dit "a=b/c avec c supérieur à zéro", c'est incorrect ?
Sans plus grande précision, "inférieur" signifie "\le" alors que "strictement inférieur" désigne "<".
C'est officiel ?
Donc, si on dit "inférieur ou égal" c'est la même chose que "inférieur", donc "égal" est superflu, inutile parce que sous-entendu ?
Cette interprétation peut se justifier sans le cas des réels, mais j'aimerais bien confirmation dans le cas des entiers.
PS. Et pour être complet dans ma question si je dit "a=b/c avec c supérieur à zéro", c'est incorrect ?
Dlzlogic a écrit:Bonjour,
C'est officiel ?
Donc, si on dit "inférieur ou égal" c'est la même chose que "inférieur", donc "égal" est superflu, inutile parce que sous-entendu ?
Cette interprétation peut se justifier sans le cas des réels, mais j'aimerais bien confirmation dans le cas des entiers.
PS. Et pour être complet dans ma question si je dit "a=b/c avec c supérieur à zéro", c'est incorrect ?
Salut, Dlzlogic. Comme Capitaine Nugget c'est comme ça que je l'ai appris, sans précision c'est "inférieur ou égal" et si on veut préciser on rajoute "stricte" !
(et peu importe que l'on soit sur les entiers, réels, rationnels, décimaux, etc.)
en français,
"inférieur à" signifie
donc "inférieur ou égal" est une redondance pédagogique si on veut,
"strictement inférieur" signifie
en français, on dit nombre "strictement positif" pour désigner
en anglais, on dit nombre "non négatif" pour désigner
Ce n'est pas que le Larousse est périmé, c'est surtout qu'il n'a jamais été une référence pour des définitions mathématiques. Voici une référence un peu plus scientifique : http://www.cnrtl.fr/definition/sup%C3%A9rieur
leon1789 a écrit:Ce n'est pas que le Larousse est périmé, c'est surtout qu'il n'a jamais été une référence pour des définitions mathématiques. Voici une référence un peu plus scientifique : http://www.cnrtl.fr/definition/sup%C3%A9rieur
Bon, alors, si c'est officiel, pourquoi ne pas l'avoir dit tout de suite ?
Finalement, je constate que les anglais ont plus de logique que nous. Ils utilisent en mathématiques les termes dans le même sens que celui du dictionnaire.
[EDIT]Par contre, je n'ai pas trouvé la signification mathématique pour "inférieur" faut-il le prendre comme contraire de supérieur, en ce cas, étant donné que supérieur doit être compris comme "supérieur ou égal" alors "inférieur" doit être compris comme "strictement inférieur".
Tu vois, malgré tes efforts, on tourne en rond.
Dlzlogic a écrit:[EDIT]Par contre, je n'ai pas trouvé la signification mathématique pour "inférieur" faut-il le prendre comme contraire de supérieur, en ce cas, étant donné que supérieur doit être compris comme "supérieur ou égal" alors "inférieur" doit être compris comme "strictement inférieur".
Tu vois, malgré tes efforts, on tourne en rond.
Oui je vois bien, malgré mes efforts, tu tiens à tourner en rond.
Inférieur est la notion "duale" de supérieur (ie x est inférieur à y lorsque y est supérieur à x), pas sa négation (ou contraire comme tu dis)... Un peu de logique que diable ! :ptdr:
Exemples :
2 est à la fois supérieur et inférieur à 2
le nombre complexe i (le i de i²=-1) n'est ni supérieur ni inférieur à 2 .
Bon, d'accord pour tout.
Simplement je plains les élèves qui feront de l'informatique en général et auront à utiliser l'algèbre de Boole en particulier.
Pour moi, dans mon langage assez primaire, il est vrai, 2 n'est ni supérieur, ni inférieur à 2, mais 2 est égal à 2.
Là on parle en nombre entiers, la même discussion en nombre réels mériterait un autre sujet. (Par ailleurs les complexes, c'est un autre chapitre. Il ne faut pas tout mélanger.)
A toi d''ouvrir la discussion sur les nombres réels, si tu veux.
Simplement je plains les élèves qui feront de l'informatique en général et auront à utiliser l'algèbre de Boole en particulier.
Pour moi, dans mon langage assez primaire, il est vrai, 2 n'est ni supérieur, ni inférieur à 2, mais 2 est égal à 2.
Là on parle en nombre entiers, la même discussion en nombre réels mériterait un autre sujet. (Par ailleurs les complexes, c'est un autre chapitre. Il ne faut pas tout mélanger.)
A toi d''ouvrir la discussion sur les nombres réels, si tu veux.
Ok, mais en maths, ce n'est pas l'informatique qui fait foi. Comme je disais plus haut, mathématiquement, pour parler de «  », il n'y a pas lieu de distinguer les entiers des réels. Et les nombres complexes n'ont pas non plus à être écartés, même s'il faut faire attention dans ce cas. Il y a également plein d'autres ensembles (et pas forcément des nombres !) qui entre dans le chapitre "Relation d'ordre".
», il n'y a pas lieu de distinguer les entiers des réels. Et les nombres complexes n'ont pas non plus à être écartés, même s'il faut faire attention dans ce cas. Il y a également plein d'autres ensembles (et pas forcément des nombres !) qui entre dans le chapitre "Relation d'ordre".
Je crois qu'il est bon de rappeler la définition mathématique "officielle" d'une relation d'ordre :
Ici E est un ensemble quelconque, il peut s'agir de l'ensemble des entiers, des réels, des complexes, ou même bien d'autres choses (ensemble d'ensembles, etc.)
Il est important de voir que la réflexivité (x x) est demandée dans la définition : c'est parce que cela doit être mathématique utile, non ? Quant à elle, la relation < n'est pas réflexive.
x) est demandée dans la définition : c'est parce que cela doit être mathématique utile, non ? Quant à elle, la relation < n'est pas réflexive.
Par ailleurs, nulle part dans cette définition, on ne demande que deux éléments de E soient toujours comparables. On parle d'ordre partiel (quand il existe non comparable, par exemple
non comparable, par exemple  , ou les parties
, ou les parties ) ) ou d'ordre total (quand tous les
) ou d'ordre total (quand tous les  sont comparables, par exemple les réels, les entiers).
sont comparables, par exemple les réels, les entiers).
Je crois qu'il est bon de rappeler la définition mathématique "officielle" d'une relation d'ordre :
Une relation d'ordre est une relation binaire réflexive, transitive et antisymétrique : soit E un ensemble et une relation binaire sur cet ensemble notée «», cette relation est une relation d'ordre si pour tous x, y et z éléments de E les trois points suivants sont vérifiés :
(1.) xx (réflexivité)
(2.) (xy et y
x)
x = y (antisymétrie)
(3.) (xy et y
z)
x
z (transitivité)
La relation binaire «» est définie par : x
y si et seulement si y
x.
Ensuite, viennent les symboles « » :
x y si et seulement si xy et x
y.
Ici E est un ensemble quelconque, il peut s'agir de l'ensemble des entiers, des réels, des complexes, ou même bien d'autres choses (ensemble d'ensembles, etc.)
Il est important de voir que la réflexivité (x
Par ailleurs, nulle part dans cette définition, on ne demande que deux éléments de E soient toujours comparables. On parle d'ordre partiel (quand il existe
Dlzlogic a écrit:Pour moi, dans mon langage assez primaire, il est vrai, 2 n'est ni supérieur, ni inférieur à 2, mais 2 est égal à 2.
Là on parle en nombre entiers, la même discussion en nombre réels mériterait un autre sujet. (Par ailleurs les complexes, c'est un autre chapitre. Il ne faut pas tout mélanger.)
Comme je disais, il n'y a pas lieu, quand on parle de < ou
Je comprends que dire "inférieur" en pensant à "
Mais je crois qu'il est bon de faire un peu de maths pour comprendre pourquoi on est arrivé à dire "inférieur à" pour "
Il faut savoir que "
Une relation d'ordre est une relation binaire réflexive, transitive et antisymétrique : soit E un ensemble et une relation binaire sur cet ensemble notée «», cette relation est une relation d'ordre si pour tous x, y et z éléments de E :
xx (réflexivité)
(xy et y
x)
x = y (antisymétrie)
(xy et y
z)
x
z (transitivité)
On associe également à toute relation d'ordre, une relation dite dordre strict notée alors < (qui n'est pas à proprement parlé une relation d'ordre puisque la réflexivité n'est pas satisfaite), qui est la restriction de la relation d'ordre aux couples d'éléments distincts :
x < y si et seulement si xy et x
y.
Existe-t-il d'autre relation d'ordre que
Il y a aussi la division
Alors quel rapport avec notre discussion ? C'est simple :
dit-on {1,2} est "inclus dans" {1,2} ? Oui
dit-on {1,2} est "inclus dans ou égal à" {1,2} ? Non
dit-on 4 divise 4 ? Oui
dit-on 4 "divise ou égale" 4 ? Non
Bref, on ne dit jamais "ou égal"... Il paraît donc assez logique de dire
2 est "inférieur" à 2
et pas 2 est "inférieur ou égal" à 2.
Quant au mot "strict", il a bien sa place dans le langage mathématique :
{1,2} est "strictement inclus dans" {1,2,3} ;
4 "divise strictement" 8
2 est "strictement inférieur" à 4
De même, on peut penser aux fonctions :
quand on parle de fonction "croissante" ( x
Bref, ma conclusion est qu'en mathématique, c'est bien plus homogène de permettre l'égalité quand on dit "inférieur à" (ou "supérieur à"), "inclus dans" (ou "contient"), "divise" (ou "est multiple de"), etc.
et d'utiliser le mot "strictement" quand nécessaire.
Oui, tout ça est fort intéressant.
Pourquoi tu dis tout cela sur un forum français, alors qu'à l'évidence, ce sont les anglais à qui tu dois apprendre ces choses là.
Il me semble que tout le monde sur ce forum a bien compris que "inférieur" veut dire "inférieur ou égal". Il n'y a que les anglais qui ne le savent pas.
Concernant la différence entre entiers et réels, on en parle quand tu veux, mais il faut ouvrir un nouveau sujet.
Petit commentaire perso : en mathématique, on peut énoncer tout ce qu'on veut, le seul critère (limite de validité) est la résolution de questions dans le monde du réel. Ne me tente pas en me demandant des exemples.
Pourquoi tu dis tout cela sur un forum français, alors qu'à l'évidence, ce sont les anglais à qui tu dois apprendre ces choses là.
Il me semble que tout le monde sur ce forum a bien compris que "inférieur" veut dire "inférieur ou égal". Il n'y a que les anglais qui ne le savent pas.
Concernant la différence entre entiers et réels, on en parle quand tu veux, mais il faut ouvrir un nouveau sujet.
Petit commentaire perso : en mathématique, on peut énoncer tout ce qu'on veut, le seul critère (limite de validité) est la résolution de questions dans le monde du réel. Ne me tente pas en me demandant des exemples.
Dlzlogic a écrit:Pourquoi tu dis tout cela sur un forum français, alors qu'à l'évidence, ce sont les anglais à qui tu dois apprendre ces choses là.
Tes remarques sont encore une fois désobligeantes...
Dlzlogic a écrit:Petit commentaire perso : en mathématique, on peut énoncer tout ce qu'on veut, le seul critère (limite de validité) est la résolution de questions dans le monde du réel.
Je préfère encore que tu parles d'informatique, cela me fait moins bondir que tes visions "décalées" sur les maths.
Dlzlogic a écrit:Il me semble que tout le monde sur ce forum a bien compris que "inférieur" veut dire "inférieur ou égal". Il n'y a que les anglais qui ne le savent pas.
Toi qui croyais que inférieur et supérieur étaient des notions "contraires", je suis bien content que tu dises que tout le monde a compris.
adrien69 a écrit:C'est vraiment brillant comme explication Léon. Tu l'as déduite par toi-même ou lue dans un bouquin et tu la paraphrases ? Si c'est un bouquin je veux bien la référence, genre vraiment. Et si ça vient de toi, eh bien bravo.
J'ai juste copié/collé la définition d'une relation d'ordre de http://fr.wikipedia.org/wiki/Relation_d'ordre.
Merci :lol3:
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
