Calcul intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Syphax
- Membre Naturel
- Messages: 55
- Enregistré le: 20 Nov 2011, 16:17
-
 par Syphax » 01 Mai 2013, 14:55
par Syphax » 01 Mai 2013, 14:55
Bonjour,
Quelqu'un pourrait m'aider à déterminer les alpha t.q l'intégrale généralisée suivante converge ?
Int entre -infini et +infini de x^alpha * C*(1+x²)^-m avec alpha > 0 et m,C réels.
Merci
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 02 Mai 2013, 08:09
par arnaud32 » 02 Mai 2013, 08:09
Syphax a écrit:Bonjour,
Quelqu'un pourrait m'aider à déterminer les alpha t.q l'intégrale généralisée suivante converge ?
Int entre -infini et +infini de x^alpha * C*(1+x²)^{-m avec alpha > 0 et m,C réels.
Merci
^{-m}dx)
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 02 Mai 2013, 08:21
par arnaud32 » 02 Mai 2013, 08:21
deja pour quelles valeurs de alpha ta fonction est elle definie sur R?
-
LaCoc6nl
- Membre Naturel
- Messages: 90
- Enregistré le: 29 Mar 2013, 19:06
-
 par LaCoc6nl » 02 Mai 2013, 13:13
par LaCoc6nl » 02 Mai 2013, 13:13
Syphax a écrit:Bonjour,
Quelqu'un pourrait m'aider à déterminer les alpha t.q l'intégrale généralisée suivante converge ?
Int entre -infini et +infini de x^alpha * C*(1+x²)^-m avec alpha > 0 et m,C réels.
Merci
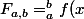dx)
est définie si la fonction

telle que :
= x^{\alpha}*C*(1+x^2)^{-m})
avec
 \in \mathbb{R^3},)
est continue sur

(où
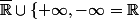)
car f est alors

-intégrable localement sur

. Si de plus
 \in \overline{\mathbb{R}})
alors

converge en
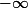
et si
 \in \overline{\mathbb{R}})
alors F converge en

. Il suffit donc de trouver pour quelles valeurs des paramètres de l'énoncé, ces limites existent (revoir
un cours sur l'intégrale généralisée)...
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 02 Mai 2013, 14:14
par arnaud32 » 02 Mai 2013, 14:14
pour faire tendre a vers -oo et b vers +oo il faudrait que Df soit egal a R
est ce la cas?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
