Marche aléatoire simple

[egan]

Salut tout le monde,

Je m'intéresse cette fois à la marche aléatoire simple sur Z.
Est-ce que vous êtes d'accord avec ça ?



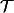
où est l'ensemble des temps d'arrêt à valeurs dans N*.

Et avec ça ?



où T est un temps d'arrêt à valeurs dans N*.

S est la marche aléatoire et X le pas.
Si un de ces résultats vous paraît correct, est-ce que vous pourriez m'expliquer comment le démontrer ? La partie en 2a-n ne me gêne pas, c'est l'autre qui m'enquiquine.

[egan]

Personne ?

[Doraki]

tu veux dire quoi par "il existe un unique ensemble {i1 ... ia} de taille <= a inclus dans [1;n] tel que Xi1 = ... = Xia = 1" ?
Est-ce que tu penses secrètement à "Xn = a*1+(n-a)*(-1) = n-2a" ?

C'est quoi exactement ton ensemble de temps d'arrêts et c'est quoi un temps d'arrêt ?

[egan]

L'évènement par rapport auquel je conditionne est l'évènement: on connait les n premiers X_i et on a obtenu exactement a fois X_i = 1.

Sinon, j'entends pas temps d'arrêt la définition classique des temps d'arrêts. J'ai juste oublié de préciser la filtration associée. C'est en fait la filatration naturelle des X_i.