Développer racine carré puissance 2
24 messages
- Page 1 sur 2 - 1, 2
Développer racine carré puissance 2
Bonjour,
Je cherche à développer :
A = (2 racine de 3 - 3)² + (racine de 27 + 1 )²
Je pense qu'il faut utiliser l'identité remarquable (a-b)² = a² - ab + b²
mais je n'y arrive pas...merci pour votre aide et joyeuses pâques :ptdr:
Je cherche à développer :
A = (2 racine de 3 - 3)² + (racine de 27 + 1 )²
Je pense qu'il faut utiliser l'identité remarquable (a-b)² = a² - ab + b²
mais je n'y arrive pas...merci pour votre aide et joyeuses pâques :ptdr:
salut !
Tout à fait !
Il faudra connaître les développement de^2) et
et ^2) .
.
Commençons par le premier terme de la somme :^2) .
.
Connaissant le forme développée de^2) , tu peux trouver celui de
, tu peux trouver celui de ^2) en remplaçant
en remplaçant  par
par 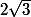 et
et  par
par  .
.
Fait de même avec^2) .
.
:+++:
IDIOTBETE a écrit:Bonjour,
Je cherche à développer :
A = (2 racine de 3 - 3)² + (racine de 27 + 1 )²
Je pense qu'il faut utiliser l'identité remarquable (a-b)² = a² - ab + b²
mais je n'y arrive pas...merci pour votre aide et joyeuses pâques :ptdr:
Tout à fait !
Il faudra connaître les développement de
Commençons par le premier terme de la somme :
Connaissant le forme développée de
Fait de même avec
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
IDIOTBETE a écrit:Bonjour,
Je cherche à développer :
A = (2 racine de 3 - 3)² + (racine de 27 + 1 )²
Je pense qu'il faut utiliser l'identité remarquable (a-b)² = a² - ab + b²
mais je n'y arrive pas...
Et pourquoi donc ?
(a-b)² = a² - ab + b²
Donc si a = 2rac(3) et b= 3 :
(2rac(3) - 3 )² = (2rac(3))² -2*2rac(3)*3 + 3²
= 4*3 - 12rac(3) + 9
= 21 - 12rac(3)
Que ne comprends tu pas ?
(x - 5)² = 9
(x - 5)² - 9 = 0
jusque là oui, tu reconnais ensuite une nouvelle identité remarquable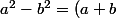*(a-b))
(x - 5 + 3) * (x - 5 - 3) = 0
tu avais remplacé le * par un - !
et là effectivement x-2=0 ou x-8=0 car la multiplication de 2 nombres est égale à 0 si l'un ou l'autre des nombres est égal à 0
dans ce cas simple tu peux facilement vérifier que les solutions 2 et 8 sont correctes :lol3:
(x - 5)² - 9 = 0
jusque là oui, tu reconnais ensuite une nouvelle identité remarquable
(x - 5 + 3) * (x - 5 - 3) = 0
tu avais remplacé le * par un - !
et là effectivement x-2=0 ou x-8=0 car la multiplication de 2 nombres est égale à 0 si l'un ou l'autre des nombres est égal à 0
dans ce cas simple tu peux facilement vérifier que les solutions 2 et 8 sont correctes :lol3:
IDIOTBETE a écrit:merci beaucoup pour les explications c'est plus facile de regrouper
a² + b² - 2 ab ou a² + b² + 2 selon les cas. Super merci encore
sinon pour le 27 + 1 + 2v27
= 30v27 ?
ou je décompose le 27 en 3 x 9 ?
Quand tu as unesomme de nombres entiers et de racines carrées, il faut additionner séparément les nombres entiers et les racines carrées
Ex :
Tu ne peux rien faire de plus car 8,
Les racines carrées peuvent être multipliées
Dans ton cas tu parles de décomposer 27 en 3*9 ... et là tu marques des points, en effet tu peux simplier
Je te laisser continuer, tu me donneras le résultat du développement de A ...
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
