Salut !
Mehdi.H a écrit:Exercice 1:Soit D la droite d'équation y=mx-2 ou m est un nombre réel. Peut-on déterminer m pour que :
1. D passe par le point A(-2;5) ?
2. D passe par l'origine du repère ?
3. D soit parallèle à la droite

' d'équation x-y+2 = 0 ?
4. D soit parallèle à l'axe des ordonnées ?
1. On ne peut pas déterminer m pour que D passe par le point A(-2;5) car le coefficient directeur de la droite d'équation y=mx-2 est positif alors que la droite

' qui passe par le point A(-2;5) a un coefficient directeur négatif.
2. On ne peut pas déterminer m pour que D passe par l'origine du repère car l'ordonnée à l'origine est -2 et non 0.
3. J'aurais besoin d'aide je n'ai pas trouvé.
4. On ne peut pas déterminer m pour que D soit parallèle à l'axe des ordonnées car elle n'a pas une équation de la forme x=c.
1°) Faux !

est un réel, or un réel peut-être négatif !
Attention, ce n'est pas parce qu'il n'y a pas de signe négatif devant

que m est nécessairement positif !

passe par le point
)
si et seulement si

appartient à

, c'est-à-dire, si les coordonnées de

vérifient l'équation de

;
2°) Oui !
3°)

et

ont pour équations réduites respectives
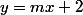
et
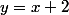
donc ces deux droites sont parallèles si et seulement si leurs coefficients directeurs sont égaux.
4°) Tout à fait !
Mehdi.H a écrit: Exercice 2:
Soit D la droite d'équation y=-x+2. Déterminer algébriquement une équation de la droite D' passant par A(1;4) et parallèle à D.
Je n'ai pas du tout compris cet exercice.
Dans cet exercice, on te demande de trouver par le calcul une équation de la droite
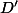
parallèle à

passant par

.
Pour cela, posons

l'équation réduite de la droite
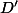
.
En traduisant mathématiquement la phrase : "
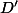
parallèle à

ET
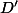
passe par

", trouver

et

revient à résoudre un système de deux équations dont les deux inconnues sont

et

:
-
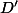
est parallèle à

si et seulement si les coefficients directeurs de

et
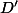
sont égaux ;
Tu obtiens une équation d'inconnues

et

;
-
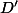
passe par

si et seulement si les coordonnées de

vérifient l'équation de
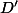
;
Tu obtiens une deuxième équation d'inconnues

et

.
:+++:
