Déterminant de Gram
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
par Supernova » 08 Fév 2013, 19:56
Salut à vous! ça fait un petit peu longtemps que j'ai posté un sujet sur ce forum, anyway, j'ai deux questions à propos du déterminant de Gram -comme le titre l'indique- qui sont les suivantes:
montrer l'égalité:
 = \frac{G(a, x_1 , ...., x_n)}{G(x_1 ,...., x_n)})
où
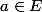
avec
))
un espace préhilibertien.
)
est libre et
)
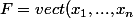et puis pour la deuxième question, on demande de
montrer par récurrence l'inégalité de
Hadamard en exploitant le fait que
 = G(x_1, ..., x_n + \alpha_1 x_1 + ....+ \alpha_{n-1} x_{n-1}))
où les
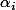
sont des réels qcq
C'est un exo très classique, j'ai essayé de faire ces deux questions mais j'ai pas pu, je voudrais donc que vous m'éclairez avec des idées, je ne veux pas voir la solution je sais qu'il y en a plein mais je veux le faire moi-même, en se servant de vos indications bien sur .
merci
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
par Doraki » 08 Fév 2013, 21:55
Comment tu ferais pour calculer d(a,F) ?
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
par Supernova » 08 Fév 2013, 23:07
Doraki a écrit:Comment tu ferais pour calculer d(a,F) ?
on décompose a = x+y où x dans F et y dans l'orthogonal de F ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 08 Fév 2013, 23:22
Bonsoir, :happy3:
Tu montres que :
 = || a - p(a) ||^{2} G(x_1 , ... , x_n ) $)
avec
 $)
la projection orthogonal de
sur
.
Il faut prendre en compte que :
 $)
 = ||a-p(a)|| $)
 $)
En général,
 = 0 \ \ \Longleftrightarrow \ \ ( u_1 , u_2 , ... , u_n ) \ $)
est une famille liée.
 $)
 \in F \ \Longrightarrow \ ( p(a) , x_1 , ... , x_n ) $)
est liée.
 $)
)
est perpendiculaire à
pour tout
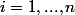
, car
est perpendiculaire à
.
Tu commences par calculer :
 = \ \dots $)
Cordialement.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 08 Fév 2013, 23:33
Bonsoir, :happy3:
Tu montres que :
avec
la projection orthogonal de
sur
.
Il faut prendre en compte que :
En général,
est une famille liée.
est liée.
est perpendiculaire à
pour tout
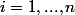
, car
est perpendiculaire à
.
Tu commences par développer :
Cordialement.
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
par Supernova » 08 Fév 2013, 23:44
barbu23 a écrit:Bonsoir, :happy3:
Tu montres que :
avec
la projection orthogonal de
sur
.
Il faut prendre en compte que :
En général,
est une famille liée.
est liée.
est perpendiculaire à
pour tout
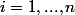
, car
est perpendiculaire à
.
Tu commences par développer :
Cordialement.
Ok barbu_23 ! merci bien pour tes indications, je crois avoir compris l'idée, c'est à moi de jouer maitenant.
Bonne nuit ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
