:hum: Désolé, je vous embète encore une fois (enfin surtout ceux qui m'ont répondu et m'ont bein aidé l'autre fois en me disant que la matrice qui m'intéréssait s'appelait matrice de Gram. Mais comme c'est une matrice qu'on a pas étudié en cours j'ai besoin de trouver uen démonstration ou preuve de la propriété qui dit que la matrice de Gram d'une famille liée => son déterminant est nul.
J'ai beau chercher sur google pas de trace de démonstration, peut être que qelqu'un d'entre vous l'a étudié... Merci pour vos réponses. :happy2:
Urgent matrice de Gram
8 messages
- Page 1 sur 1
Ah et j'avais oublié il y a aussi le fait que cette matrice de Gram peut s'écrire sous la forme G=tP.P (y a t'il un lein avec Cholesky ? ou plutôt la formule de changement de base mais avec P symétrique (tP=P^(-1)) et la matrice identité ce qui donnerait P^(-1).Id.P <=> tP.Id.P <=> tP.P ?)
merci sincèrement de votre aide... :hein:
merci sincèrement de votre aide... :hein:
On a n vecteurs 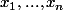 et on pose
et on pose 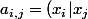) . La matrice des
. La matrice des 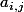 se note
se note ) .
.
Si la famille) est liée, alors on a une combinaison linéaire nulle des
est liée, alors on a une combinaison linéaire nulle des  à coefficients non tous nuls :
à coefficients non tous nuls :
 . On va en déduire immédiatemment une relation entre les lignes de la matrice.
. On va en déduire immédiatemment une relation entre les lignes de la matrice.
On a donc pour tout j :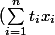|x_j=0) ,
,
c'est-à-dire :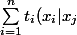=0) ,
,
soit .
.
Les lignes de la matrices sont donc liées. Son déterminant est nul.
La réciproque est tout aussi évidente.
Si la famille
On a donc pour tout j :
c'est-à-dire :
soit
Les lignes de la matrices sont donc liées. Son déterminant est nul.
La réciproque est tout aussi évidente.
Claracat a écrit:Ah et j'avais oublié il y a aussi le fait que cette matrice de Gram peut s'écrire sous la forme G=tP.P (y a t'il un lein avec Cholesky ? ou plutôt la formule de changement de base mais avec P symétrique (tP=P^(-1)) et la matrice identité ce qui donnerait P^(-1).Id.P tP.Id.P tP.P ?)
merci sincèrement de votre aide... :hein:
Attention : symétrique c'est t(P)=P (et pas P^(-1)). L'égalité t(P)=P^(-1) est pour les matrices orthogonales.
De plus, ici c'est G qui est symétrique. On sait qu'une matrice symétrique (réelle) est diagonalisable dans une base orthonormée. Ce qui s'écrit :
G=t(Q)DQ où D est diagonale et Q est orthogonale. Si les valeurs propres de G (donc les éléments diagonaux de D) sont positives, on peut écrire D=T² ou T est la matrice diagonale dont les éléments diagonaux sont les racines carrées de ceux de D. D'où G=t(Q)T²Q=t(Q)t(T)TQ=t(TQ)TQ=t(P)P en ayant posé P=TQ. Cela répond à la question lorsque les vp sont positive. Est-ce toujours le cas pour une Gram? Je ne vois pas de raison à cela.
Merci pour vos réponses et j'ai un élément de réponse pour le valeurs propres positives, c'est un résultat que j'ai dans mon cours d'analyse numérique:
si A est une matrice symétrique réelle définie positive alors A ets inversible et toutes ses valeurs propres sont réelles et strictement positives !!!
Voili Voilà merci encore à un prohaine peut être :king2:
si A est une matrice symétrique réelle définie positive alors A ets inversible et toutes ses valeurs propres sont réelles et strictement positives !!!
Voili Voilà merci encore à un prohaine peut être :king2:
Claracat a écrit:si A est une matrice symétrique réelle définie positive alors A ets inversible et toutes ses valeurs propres sont réelles et strictement positives !!!
C'est évident que "définie positive" entraine vp>0. Mais une Gram n'est pas définie si les vecteurs x1,...xn sont liés et je ne vois pas de raison pour qu'elle soit positive.
Pour une matrice de Gram, le coefficient d'indices (i,j) vaut  = ^tX_i X_j) (où
(où  est le vecteur colonne contenant les coordonnées de
est le vecteur colonne contenant les coordonnées de  dans la base canonique (donc orthonormée)). Si P est la matrice dont les colonnes sont les
dans la base canonique (donc orthonormée)). Si P est la matrice dont les colonnes sont les  , on a
, on a  (Si A et B sont deux matrices quelconques (enfin, il faut pouvoir les multiplier), le coefficient (i,j) de AB est le produit de la i-ème ligne de A par la j-ème colonne de B).
(Si A et B sont deux matrices quelconques (enfin, il faut pouvoir les multiplier), le coefficient (i,j) de AB est le produit de la i-ème ligne de A par la j-ème colonne de B).
Une matrice de la forme est toujours symétrique positive (pour la positivité, on a
est toujours symétrique positive (pour la positivité, on a  = (^t(^tP)X|PX) = (PX|PX) \geq 0) ). Une matrice symétrique positive a ses valeurs propres positives (strictement positives si la matrice est définie positive). Pour le voir il suffit de prendre un vecteur propre
). Une matrice symétrique positive a ses valeurs propres positives (strictement positives si la matrice est définie positive). Pour le voir il suffit de prendre un vecteur propre  pour la valeur propre
pour la valeur propre  , on a
, on a  \geq 0) et
et = \lambda (X|X) = \lambda ||X||^2) .
.
Une matrice de la forme
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
